基于深度学习理念，探究单元整合教学

杨怡 喻巧月

【摘 要】深度学习是一种课堂变革的理念和课堂教学的设计思路。深度学习倡导单元学习。苏教版数学三年级上册第四单元“两、三位数除以一位数”，学习的核心内容是“除数是一位数的除法”，而作为单元开启课“口算除法”则是后续学习笔算除法的基础。本文基于深度学习的理念，尝试以单元整合的教学方式，从“基于学情，尝试课时整合;定位教学目标，构建教学路径;剖析教学过程，实现深度学习;对比课堂结构，反思深度教学”这四个方面进行教学尝试和思考。

【关键词】深度学习 单元整合 口算除法 运算能力

在深度学习的课堂中，学生对所学知识能进行整体理解，能促进知识的建构和方法的迁移，有助于深刻性思维的发展，在解决问题的过程中培育核心素养。基于深度学习理念，苏教版数学三年级上册第四单元“两、三位数除以一位数”的学习主题就是除法的运算方法的探究，以及在探究过程中反映的数学核心素养，重点培养学生的除法运算能力和推理能力。

口算除法是笔算和估算的基础，也是后续学习竖式计算、理解算理的铺垫。从深度学习的理念出发，本节课的核心可以理解为：在教师的引领下，实现让学生全身心积极参与、体验成功、获得发展的数学学习，从而提高学生的口算技能和思维能力，发展学生的核心素养。

在教学中，如何通过单元整合教学，将深度学习理念融入口算除法的教学中，实现上述核心目标呢？笔者从以下几点进行论述。

一、基于学情分析，尝试课时整合

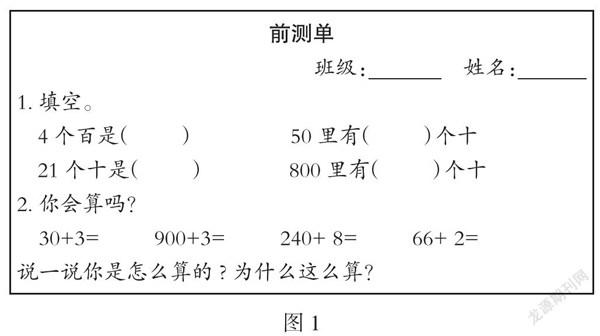
为了更有效地实施单元整合教学，把握学生对于本节课知识的现实起点，笔者将教材例题和练习中的算式稍做修改后作为前测题目（见图1），鼓励学生用自己的方法进行口算，并将口算的想法和理由通过画图或口述表达出来。

（一）“高数据”反映出学生的“高起点”

整十数除以一位数的口算正确率达到100%，整百数和几百几十的数除以一位数的口算正确率在80%到95%之间，学生的现实知识起点较高。两位数除以一位数（每位都能除尽）的口算正确率也达到85%以上，说明学生能自主依据表内除法的知识经验进行口算，已具备初步的推理能力。同时，笔者从部分教师的访谈中还了解到，在竖式计算的教学中，学生由于能直接口算出结果，往往会出现一步完成计算的错误情况。

（二）学生对于算理的理解很模糊

在陈述算法、解释算理的测试中，虽然有超过70%的学生能注意到“0”的变化，通过观察到的数字特点来说出大概的算法，但对于背后的算理几乎没有一个学生能够说清楚。

基于以上学情分析，学生已有较高的现实起点，教材中“小步子渐进”的编排方式显然降低了学习的挑战性，且与学生的现实起点不相匹配。因此，笔者从单元的整体视角进行设计，将教材中本单元的前三个例题进行改编、整合为一节单元开启课，确定本节课的教学重点是梳理和沟通口算的算理和方法，培养学生的运算和推理能力，为笔算除法打下基础，以单元整合为手段，构建数学深度学习的课堂;教学难点是引导学生在动手操作和抽象说理的过程中，感悟算理、明晰算法，进行深度学习。

二、定位教学目标，构建教学路径

本节课的教学目标定位在三个维度。第一维度：知识目标。通过创设平均分的具体情境，以任务驱动的方式，经历探索口算除法的过程，主动理解算理，拓展表内除法，理解并掌握细分计数单位的计算方法。第二维度：能力目标。在探索算法的过程中，学生能应用已有知识交流算法，提升转化、推理等思维能力，积累相关的计算经验，发展深刻性思维。第三维度：素质目标。在动手、说理的深度学习中，积累丰富的数学活动经验，学会更清晰、更深入、更全面地思考问题，促进学生的持续发展。

为达成以上教学目标、突出重点、突破难点，笔者主要采用了两条教学路径。路径一：任务驱动。先直面问题、独立思考，再进行说理交流、思维碰撞，提出问题、全班互动，让学生经历学习的全过程。路径二：沟通关联。学生在反复沟通图与式的过程中，探索并内化计数单位细分的计算方法，拓展表内除法的学习经验，掌握利用乘法口诀求商的算法，理解算理，让思维从直观逐步走向抽象，探寻深度学习路径。

三、剖析教学过程，实现深度学习

（一）任務驱动，创设深度学习空间

鉴于前测中学生高水平、低理解的现实起点，笔者提供了精心设计的学习单和学具，给予学生独立思考的时间和充分探究的空间。学生可借助小棒、人民币等现实模型，赋予除法计算的现实意义。

（二）思维碰撞，探究深度学习路径

1.数形结合，建立算理模型

在交流60÷3的口算中，学生边操作边说理，通过图和式的沟通（见图2），初步体会把60看成6个十，6个十除以3就得2个十，形成算理的初步感知。

2.说理辨析，深入算法本质

对于69÷3这道改编自除法笔算的例题，很多学生都会表达自己的直观算法：6÷3=2，9÷3=3，所以69÷3=23。通过摆小棒的过程，学生进行质疑、辨析，在思维的碰撞中，逐步理解算理的本质：6除以3实际是6个十除以3。由此形成两位数除以一位数口算的算法结构：先把两位数拆成几个十和几个一，分别除，最后再把得数合起来，从而深入理解算法的本质。

3.转化迁移，拓展算理结构

在剖析120÷3时，学生依据学习材料中的现实情境，用人民币模型说理：一张100元和一张20元无法平均分成3份，可以换成12张10元，平均分成3份，每份是4张10元。实际情境中换钱的过程，就是计算时将计数单位进行细分的过程，1个百就是10个十，把120看成12个十。将两位数除以一位数的口算算理转化迁移到几百几十的数除以一位数中，提升学生转化、推理等思维能力。

4.对比分析，形成算法模型

通过对比3道题的口算过程，建立算理的沟通：都是看成几个十或几个十和几个一来分别除，形成算法模型。

（三）融会贯通，尝试深度习题设计

深度学习中的习题设计，应有意识地把知识性、发展性、趣味性有机结合。基于以上想法，笔者精心设计了以下三组具有思维梯度的习题。

1.口算小能手——提升技能

通过快速口答的形式，让学生在题组的对比练习中提升口算技能（见图3）。

2.趣味编题——拓展应用

对照口算练习，讨论以下问题：

（1）你能说说快速口算800÷4的好方法吗？

（2）几千几百除以一位数是怎样口算的？

（3）你能仿照上面图3的题目，编几道口算题考考大家吗？

通过形式多样的练习形式，在提升计算趣味性的基础上，让学生灵活运用知识，培养学生归纳总结的能力，拓展思维的深度。

3.作业设计——单元延伸

课堂是学习的主场地，一堂课结束了，但学习并未停止，思考还未完待续。笔者设计了如图4的课后作业：

跳出枯燥的计算练习模式，取而代之的是形式多样的作业设计。这样可以提升学生的数学学习热情，同时也串联起下一节笔算除法的学习，促进算理的衔接，凸显除法计算的本质，形成单元学习路径。

四、对比课堂结构，反思深度教学

在深度学习的课堂中，学生通过“联想与结构”的学习方式，使经验与知识相互转化;以“活动与体验”为运行机制，真正实现以学为中心的教学;在“本质与变式”的转化中，尝试对学习对象进行深度加工，对学习材料进行深度整合。正如本节课，学生在数形结合的动手操作中建立算理模型;在相互说理辨析中，深入探究算法本质;利用经验与知识的转化迁移，拓展算理结构，形成算法模型。学生学会关联的学习、融通的把握、整体的建构，从而使深度学习真正发生。