基于动态等效电路模型的阀控铅酸电池放电行为参数提取研究

杜 珂，覃 剑，黎铭洪，徐开仁

（广西电网有限责任公司 南宁供电局，南宁 530000）

0 引言

阀控式铅酸（valve-regulated lead acid，VRLA）蓄电池拥有可完全回收、维护简单的特点，大量使用在园区能源互联网等领域中［1—3］。然而，铅酸蓄电池在充放电过程中，易出现欠压、过压等问题［4］。

为了对储能设备的性能做出基于应用的评价，需要在电池充放电过程中，提取温度、非线性参数以及无法直接测量的容量等参数，从而实现电能供给侧功率流管理，并对电池参数信息以及电池的动态行为进行优化。因此，构建一个合适的电池模型是实现电池非线性参数提取的重要保障［5］。

近年来，研究人员通过电化学模型［6］、数学模型［7］和电气模型［8—9］对电池参数进行了研究。其中，电化学模型基于电解液浓度、电流、电压等参数，通过一系列实验，捕获了电池所有电化学反应，并对这些参数进行估算。但电化学模型使用了各种未知的参数，计算过程呈非线性，导致其在能源互联网现场的实施存在一定难度［10—11］。数学模型主要采用经验公式预测电池充电状态（state of charge，SOC）、运行时间等参数［12—13］，但这些参数需通过求解系统方程获得，计算过程十分复杂。

蓄电池等效电路模型（equivalent electric circuit model，EECM）由静态部分和动态部分组成。静态部分表示电池化学成分的热力学性质，即电池容量和开路电压（open circuit voltage，OCV）。动态部分则表示电路的内部电阻特性，是电路充放电行为捕捉和仿真的关键。该模型的优点是与电池内部的电化学过程没有过多的联系，因此可以采用EECM对任意类型的电池进行建模，这有利于对VRLA 电池非线性放电行为的研究［14—15］。

本文提出了一种新的动态等效电路模型（dynamic equivalent electric circuit model，DEECM），该模型基于电、热、非线性行为和温度估计等因素，研究不同放电速率对电池容量的影响，电池的非线性参数与电池电流和开路电压有关的函数，以及电池温度对内部参数的影响，并通过实验验证了该模型的效果，为能源互联网储能设备的改进提供了新颖的思路。

1 动态等效电路模型

VRLA 电池的DEECM 内部电路结构如图1 所示。该模型不仅考虑了电池的电热行为，还确定了充电状态SOC，开路电压OCV，端电压Vter及电池的内部电阻Rint。图1 中，Rd为放电期间的内阻；Rd1为放电期间的过电压电阻；Rself为自放电电阻；Rint为放电期间的总内阻，Rint(n)=Rd+Rd1；C1为过电压电容；idis为电池放电电流；VC1为电容C1两端电压；iself为自放电电流。热模型由能够捕捉动态行为的Rd1C1组成，用于估算电池温度Tbat。Dd、Dd1为二极管，起指示电流方向的作用。

图1 电池放电期间的动态等效电路模型Fig.1 Dynamic equivalent electrical circuit model during battery discharging period

1.1 电气模型

图2为电池的动态等效电气模型。此模型提供了电池参数的有关信息，例如SOC、OCV、温度Tbat和内部参数。

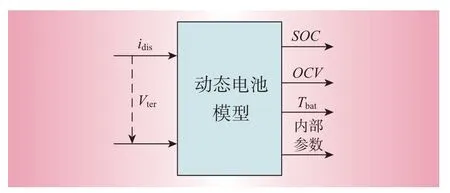
图2 电池的动态等效电气模型Fig.2 Dynamic equivalent electrical model of a battery

在充放电期间，电气模型可捕获电池的终端电压、开路电压和充电状态。

电池的端电压Vter可表示为

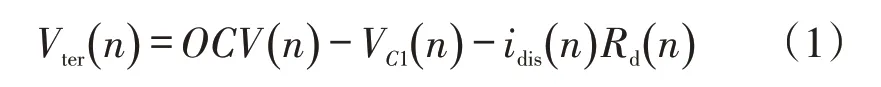
电池SOC可以通过安培小时法［16—17］估算，可表示为

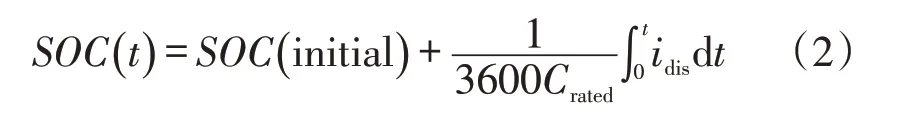
式中：SOC（initial）为电池初始SOC；Crated为电池的额定容量。

采用制造商数据表中的曲线拟合方法，可以进一步得到OCV［18—19］

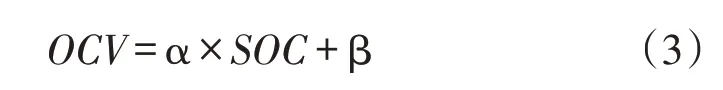
式中：α、β 均为常数。OCV和SOC的线性近似在10%到90%之间有效，若超出上述范围，OCV和SOC之间的关系不是线性的。因此，在本文的分析中，SOC默认在10%～90%。

1.2 热模型

热模型用于测量电池的内部温度，在充放电过程中温度有着重要的意义。电池内部产生的总热量分为两部分［20］，分别是由焦耳和对流损耗而产生的热量。

焦耳在电池内部产生的热量Hgen为

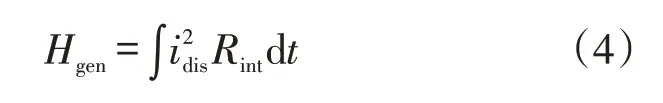
牛顿冷却定律为

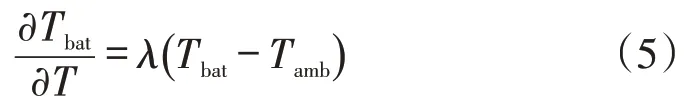
式中：Tbat为电池温度；Tamb为环境温度；λ为冷却速率。

根据式（5），若在连续时域的微控制器中将式（4）用作估计器，需要对其进行离散化处理，如

式中：ts为采样时间；Trise为电池上升的温度；m为电池质量；Sp为比热容。

根据式（7）和式（8），有

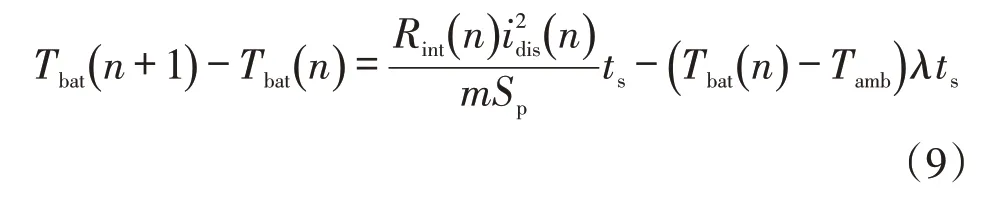
式中：A为电池面积；h为传热系数。

表1 列出了VRLA 电池的规格，该规格取自电池数据表和标准教科书［21—22］。

表1 VRLA电池参数Table 1 VRLA battery parameters

2 测试程序和参数提取

2.1 测试程序

在此测试过程中，分别对2 节200 Ah，2 V 的VRLA电池进行测试。在每个电流水平的恒流放电下，测量电池的终端电压、温度和放电状态。电池放电行为的测试步骤如图3所示。

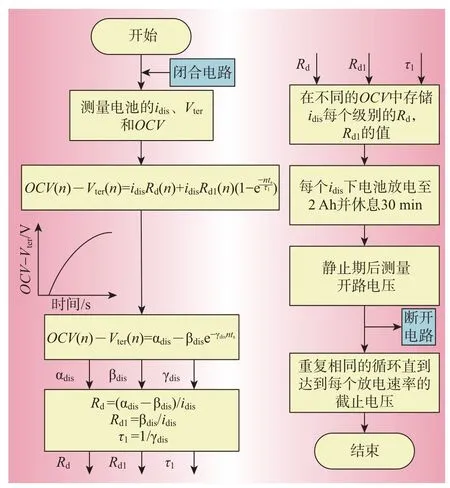
图3 电池放电行为测试步骤Fig.3 Test procedure of battery discharging behaviour

2.2 参数提取

在放电过程中，等效内部电阻Rint表示为

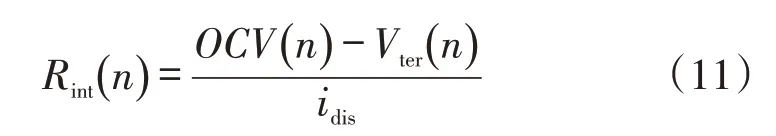
放电方程为

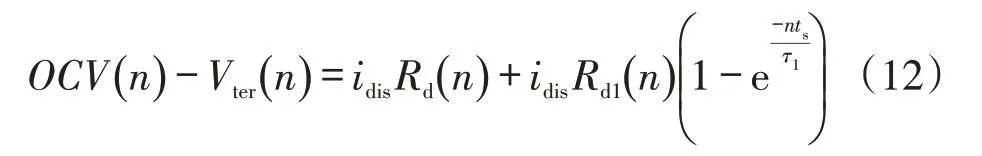
式中：τ1为时间常数。

通过式（12）的曲线拟合，可得

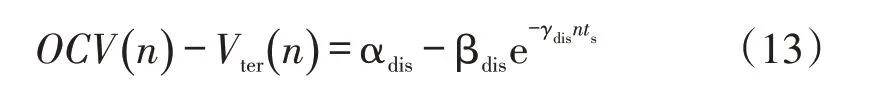
从式（12）和式（13）中提取出每个恒流放电曲线的3 个参数Rd，Rd1和τ1。根据实验结果，通过曲线拟合法求出常数αdis，βdis和γdis。每个放电电流水平下的参数为

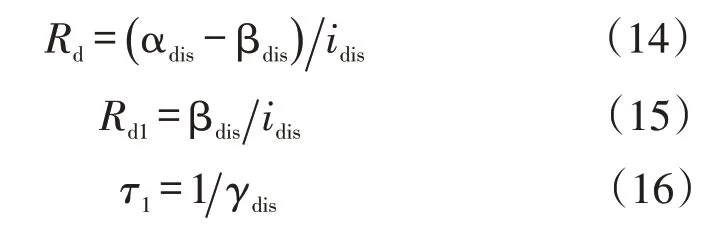
由图3 可知，根据每个电流水平，常数αdis、βdis和γdis在不同的OCV下被存储和更新。

2.2.1 内部电阻Rd

在每个放电速率下，Rd假定为开路电压的常数。表2 为电池放电过程动力学模型常数。如图4所示，Rd由电池电流的指数函数拟合为

式中：aod和bod为表2 中列出的常数。从图4 可以明显看出，电流对电池的内阻有很大影响，随放电电流的增大，内阻大幅度减小。

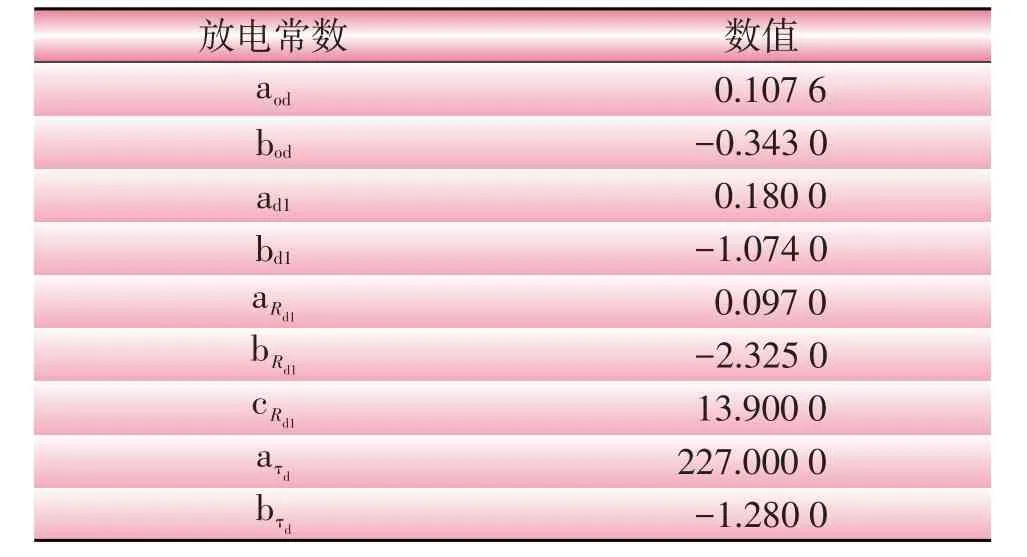
表2 放电过程动力学模型常数Table 2 Constants of dynamic model during discharging

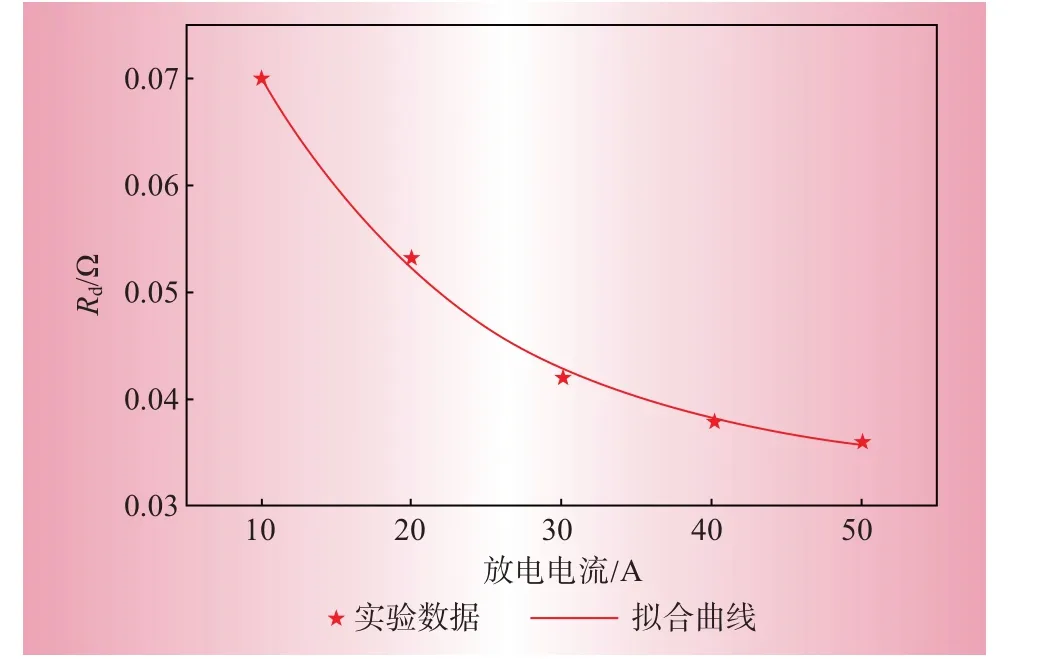
图4 Rd 的指数拟合Fig.4 Exponential fitting of Rd

2.2.2 过电压电阻Rd1

如式（18）所示，电阻Rd1受电池放电电流和开路电压的影响，表示为

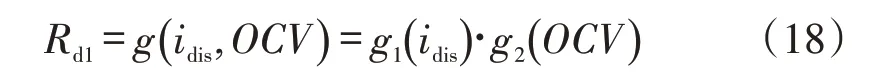
通过二次函数对Rd1开路电压的变化进行拟合，如图5所示，其误差为±2%，表示为

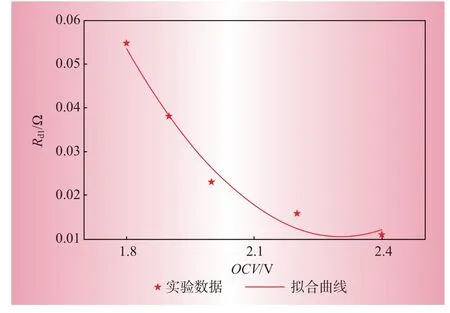
图5 Rd1曲线拟合结果Fig.5 Curve fitting result of Rd1

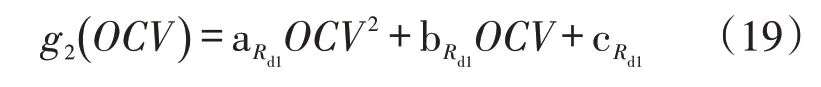
式中：aRd1、bRd1和cRd1为表2中列出的常数。

通过指数函数对Rd1电流的变化进行拟合，如图6所示，表示为

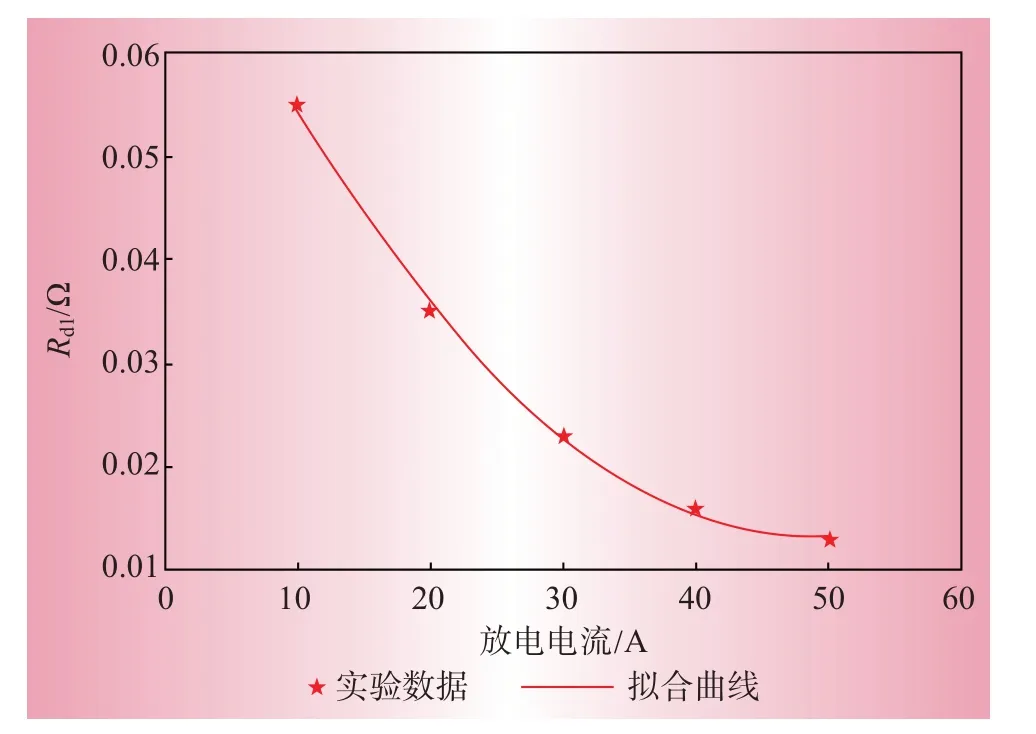
图6 Rd1 的指数拟合Fig.6 Exponential fitting of Rd1

式中：ad1和bd1为表2中列出的常数。

2.2.3 时间常数τ1

从实验结果中提取出不同大小的时间常数τ1，并对放电电流呈指数拟合，如图7所示，可表示为

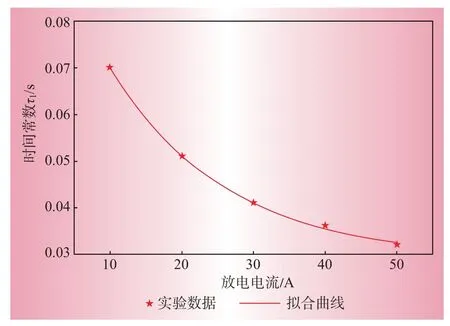
图7 不同放电电流水平下τ1 的指数拟合Fig.7 Exponential fitting of τ1 on different discharging current levels

式中：aτd和bτd为表2中列出的常数。

2.3 过电压电容

过电压电容可以根据时间常数来计算，表示为

根据文献［20］中的数据表，所有放电速率的瞬态在1 min内衰减。

2.4 电池温度对内阻的影响

温度在电池的整体性能中起着重要作用。图8显示了温度对电池内阻的影响。由图8 可知，随着电池温度的升高，电池内阻上升。

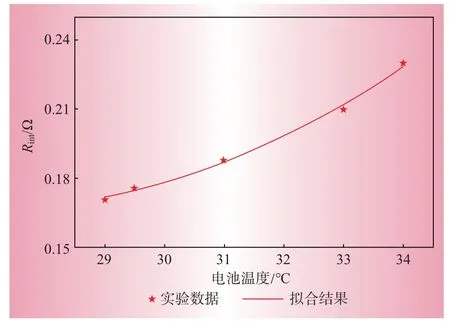
图8 温度对电池内阻的影响Fig.8 Effect of temperature on battery internal resistance

通过二次多项式函数来拟合放电过程中电池温度对电池内阻的影响，表示为

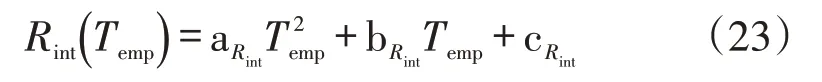
式中：Temp为电池放电温度；aRint=0.0013；bRint=-0.071；cRint=1.138。

2.5 非线性动力学模型

通过分析Rd、Rd1和τ1的方程，得到了放电行为的非线性动力学模型，即

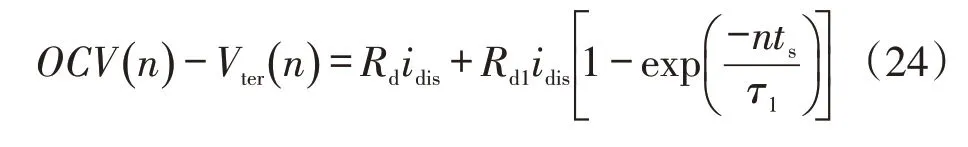
终端电压可表示为

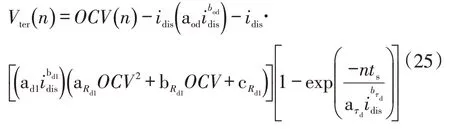
式（25）用于非线性元件的实时计算。

该非线性动态模型在系统设计中非常重要，可估计电池端电压的变化范围，以确保其与同一母线上的其他设备兼容。

3 模型验证

单个阀控式铅酸蓄电池电压为2 V，将多个电池进行串联，从而满足能源互联网的供电需求。图9为实验电池的实物图。

图9 实验电池实物Fig.9 Real object of experimental batteries

试验在南方电网某局电源实验室进行。试验时，放电电流为20 A，放电时间为10 h。同时引入VRLA 电池的二阶RC 等效电路模型作为对比模型，在相同运行条件下对两个模型进行实验验证。将DEECM 估算的端电压响应与实验中测得的电压响应进行了比较，验证该模型的准确性。

图10 为本文计算值与实测值曲线的实验验证对比图。由图10 可知，DEECM 获得的端电压变化与实验测量Vter的误差仅为0.019%，而二阶RC电路等效模型的误差为0.020%。因此，本文的DEECM在参数提取及预测能力上具有更高的准确性。

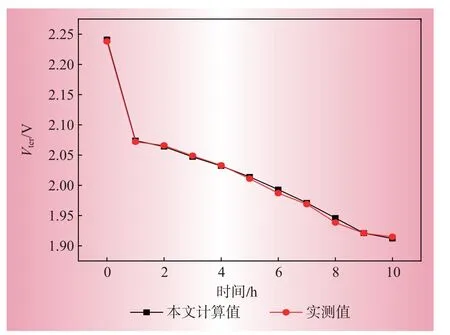
图10 实验验证Fig.10 Experimental verification

4 结束语

本文以2 V、200 Ah的阀控式铅酸蓄电池为研究对象，基于非线性动态等效电路模型研究了不同放电速率对电池容量的影响、非线性参数与电池电流和开路电压有关的函数、电池温度对内部参数的影响。通过实验验证，本文研究结果对园区能源互联网中储能电池的状态评价与智能运维具有重要意义。