L频段紧凑型FSS的研究与设计

宋倩+袁良昊+汤炜

【摘 要】本文设计了一种新型紧凑的贴片型（带阻型）频率选择表面，该频率选择表面的周期单元由双环及连接贴片构成。本文通过对方形环的等效电路进行分析，合理分布金属贴片的位置，使得频率选择表面具有较小的周期尺寸，能够较好地抑制高阶模的产生，并增加插入损耗。利用HFSS软件对该频率选择表面进行优化，对不同角度的入射波进行仿真，结构体现出较好稳定性。最后通过实验测试，所得结果与仿真结果较为吻合，-15dB插入损耗覆盖整个L频段。

【关键词】频率选择表面；L频段；等效电路

【Abstract】A novel compact stop-band FSS structure is proposed in this paper. The FSS is consist of two square loops with different sizes and four metal patch to link the loops. The physical length and other parameters of the patches is optimized by equivalent circuit method and the commercial software HFSS. The final unit has a compact structure to reject the high floquet mode and surface wave. Moreover， the sample FSS is fabricated， and the measurement result is agree with the simulation， which S21 is below -15dB over the L-band.

【Key words】FSS； L-band； Equivalent circuit

0 引言

频率选择表面（FSS）一般是由大量无源谐振单元组成的单屏或多屏周期性阵列结构，并由周期性排列的金属贴片或金属屏上孔径单元来实现的。当电磁波照射这种结构时，它可以在单元谐振频率附近呈现全反射（贴片型）或全透射特性（孔径型）。因为FSS其独特的频率选择特性，使得它越来越多的应用于国防军工中，如美国最先进的战斗机F-22，它的雷达天线罩采用FSS 来降低雷达散射截面。但建立准确的物理模型以及分析上都有一定难度，一般采用数值方法进行分析[1]。

目前，构成频率选择表面的单元形式大致可分为四类：第一类是中间连接的N极子单元，包括十字交叉振子、耶路撒冷十字、风扇型以及三极子型[2]；第二类是环型单元，包括圆环、方形环和多边形环等同心环类型[3]；第三类是内部实体单元，包括矩形贴片、圆形贴片和多方形贴片[4]；第四类是组合单元，这类单元形式由上述基本单元形式组合演化而形成。不同类型的FSS，其性能也不相同。对于FSS的性能描述一般有带宽，角度稳定性，交叉极化电平等；环形单元相对具有较好的频率稳定性，交叉极化电平相对较小，带宽相对比较大。

本文设计新型的组合单元，选择方形环作为基本单元进行优化设计。首先，设计FSS时必须综合考虑设计目标的中心频率、带宽、角度稳定性、极化稳定性、多频带和设计的难易程度等指标，并根据指标来确定周期单元形式。其次，要选择合适的单元间距，主要避免Wood奇异和栅瓣两个特殊现象发生，所以应使单元间距尽量小。最后，加载合适的介质，介质不仅是频率选择表面的依托材料，同时还可以改善FSS的性能。所以，在进行设计时，必须加载合适的介质层。而对于FSS的研究方法主要是解析方法，如准静态场理论，等效电路法和变分法。

本文在FSS的理论分析及环形FSS等效电路基础上，利用计算电磁学的商业软件ANSYS HFSS，设计了L频段内紧凑型的频率选择表面。该频率选择表面的实测结果表明，在频带1-2GHz内的S21<-15dB。并且当入射波的角度从0°到80°发生变化时，该FSS极化也是比较稳定的。

1 FSS设计的理论基础

1.1 Floquet定律

1.2 等效电路法

等效电路法（Equivalent Circuit Method）是一种经常用来分析周期结构的近似方法。它将频率选择表面单元与其相邻单元之间的相互作用等效为集总器件，进一步得出等效的电路参数，并以此便可以很容易地计算出 FSS 的传输系数和反射系数。这种分析方法直观、简便，能够快速的计算出 FSS 的谐振频率和带宽等信息[6]。图2（a）是方环型FSS周期单元结构。p是周期FSS单元的边长，g是周期单元之间的间距，w是边的宽度，d是方形环的边长。单方形环单元阵列的等效电路如图2（c）所示。ECM 计算结果的精确度随条件w=p，g =p，p =λ而变化；如w/p越小，则ECM计算的结果就越精确。当g =p 时，可以认为此时方环单元的宽度为2w，则方形环FSS单元的归一化感抗表达式为：

1.3 单元尺寸

引言中介绍传统的FSS单元形式都是基于谐振的金属单元，因此FSS谐振时的导波波长决定了单元的尺寸大小；这里的导波波长是指考虑介质加载效应之后的波长。由天线相关理论可知，对于自由空间中偶极子发生谐振时，单元的尺寸应为其半波长的整数倍；所以贴片型偶极子FSS的谐振尺寸应大体相同。但是由于相邻FSS单元之间会发生耦合，其谐振长度应略小。对于环形单元，由于末端电势相同，通常将其看做末端连接的弯折形偶极子，故其发生谐振时，环的周长为一个导波波长。

1.4 组阵方式与阵元间距

FSS 的组阵方式一般为矩形栅格与等腰三角形栅格，这两种方式的排列主要是为避免出现栅瓣和表面波。在FSS设计中，阵元间距是一个重要的参数，它不仅与阵列周期有关，而且对FSS的入射角度的稳定性、谐振频率和工作带宽都有很大的影响。一般可以通过减小阵元间距来增强 FSS 相邻单元之间的能量耦合，进而降低 FSS 的谐振频率，展宽FSS的工作带宽。另外，为了减小FSS单元尺寸，可以利用集总电抗元件加载或对FSS单元进行弯折处理，进而改善FSS 的入射角度稳定性、谐振频率和工作带宽。

1.5 介质特性

在实际的工程应用中，通常都会将 FSS 的金属周期结构印刷在介质基板上，便于减小单元尺寸和增强 FSS 的机械强度。介质加载对FSS传输特性的影响主要有下几个方面[8-9]

2）影响带宽。因为FSS介质层的波阻抗与自由空间的波阻抗不匹配，这就会使入射电磁波在两者分界面上产生反射；要想产生完全透射，必须要求介质板厚度为入射波的半个有效波长。当贴片型FSS介质层厚度小于λg/4时，介质层的反射波与金属贴片的反射波相互叠加可以展宽带宽。但由于孔径型 FSS与贴片型FSS的工作原理不同，其介质层所产生的反射反而降低了它的透射带宽。当介质层的厚度逐渐增至λg/2时，则由半波夹层的工作原理可知空气与介质分界面上没有反射现象，所以贴片型FSS的反射带宽减小而孔径型FSS的透射带宽却增加了。

3）改善入射角度稳定性。当入射平面电磁波的角度逐渐增加时，自由空间中的无介质加载FSS金属屏的谐振频率会产生一定的偏移，并且有效工作带宽会有所减小。根据Snall定理可知，当加载介质层后，介质层所产生的折射会减小 FSS 金属屏上的平面电磁波的等效入射角度，进而使得在平面电磁波斜入射时，加载介质层FSS的传输响应比无介质加载FSS的更接近于法向入射，即介质层的加载可以在一定程度上有稳定谐振频率和带宽的作用[10]。

2 双环连接型FSS的设计

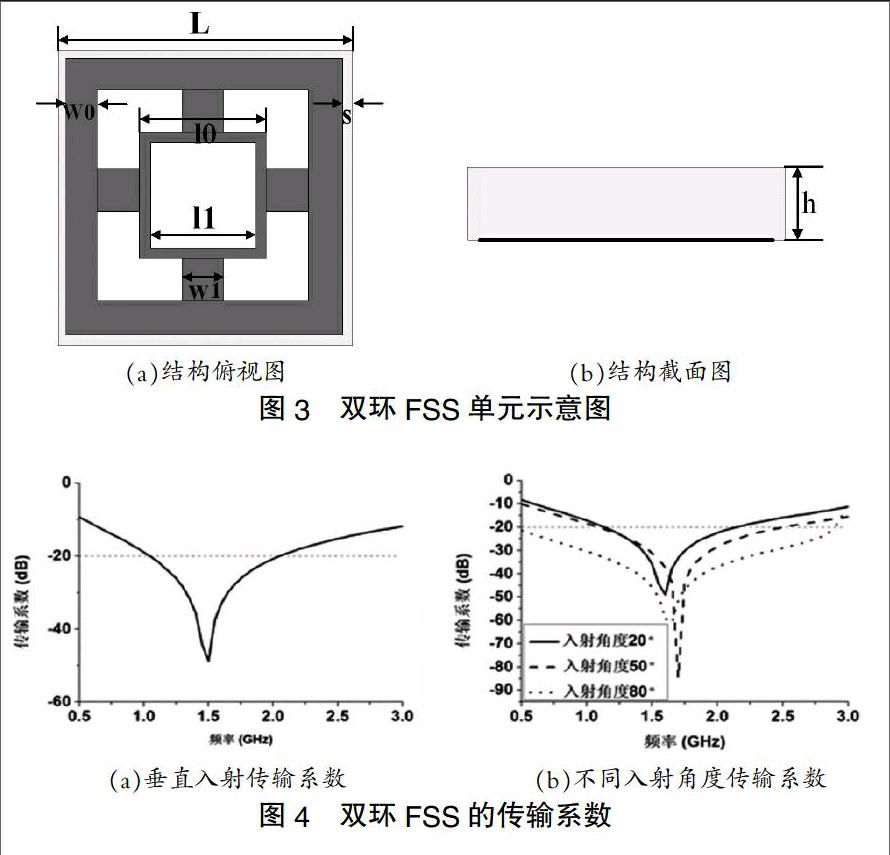
综合上述设计FSS的影响因素，根据设计指标要求在频带1-2GH时，FSS的S21<-20dB，再结合介质加载形式来优化单元尺寸，以及结合入射电磁波的角度与极化方式来优化单元尺寸和单元形式。介质板是选用厚度h=3mm且介电常数εr=3.7玻璃钢。利用HFSS最终优化的模型结构如下图3所示，其结构参数为：L=33mm，l0=16.8mm，l1=15.4mm，w0=3mm，w1=3.7mm，s=0.1mm，h=3mm。

从图4（a）中可以看出改进后的双环FSS在频带1-2GHz内的S21低于-20dB，其带宽约为67%。从图4（b）中可以看出S21随着入射波角度由20°-80°改变的时候，它的中心频率极化是较为稳定。如下图5（a）所示，是加工的双环连结型FSS的天线罩实物图；图5（b）是测试的传输系数与仿真的对比图，可以看出在1-2GHz频带内，传输系数低于-15dB，与仿真结果有一定的误差。这可能是由图5（a）中在天线罩内贴FSS不规则所导致的加工误差。

3 结论

本文设计了一种L频段紧凑型频率选择表面，仿真结果显示它在L频带内，其传输系数低于-20dB，实测的传输系数是低于-15dB的，相对带宽为67%。频率选择表面对1-2GHz电磁波显示全反射现象，实现滤波的功能。周期单元尺寸为33mm（0.165λ），结构紧凑，有利于抑制表面波。同时，仿真结果显示该FSS具有入射角的不敏感性，有利于工作较为复杂的工作环境。

【参考文献】

[1]经纬，魏兴昌，戴高乐.一种新型小尺寸宽带的频率选择表面设计[J].微波学报，2012.

[2]卢俊，张靓，孙连春.Y形和Y环形单元特性的实验对比研究[J].光学精密工程，2005（02）.

[3]T K Wu. Frequency selective surfaces and Grid Arrays[M]. New York：Wiley，1995.

[4]马金平，焦永昌，毛乃宏，陈国瑞.圆环单元频率选择表面的优化设计研究[J]. 西安电子科技大学学报，1999（06）.

[5]汤炜，刘禹杰，武菲菲.基于接收天线理论的微波吸波层设计研究[J].电波科学学报，2015，30（2）.

[6]侯新宇，崔尧，张玉英，王旭刚，刘海军.应用等效电路模型的频率选择表面有效分析[J].西北工业大学学报，2006，24（6）.

[7]王焕青.等效电路法分析频率选择表面的双频特性[J].系统工程与电子技，2008，30（11）.

[8]B.A. Munk. Frequency-selective surfaces： Theory and design[M]. Wiley， New York， 2000.

[9]J. R. Montgomery. Scattering by an infinite periodic array of thin conductors on a dielectric sheet[J]. IEEE Trans. Antennas Propag.， Jan. 1975， 23（1）： 70-75.

[10]郑书峰.频率选择表面的小型化设计与优化技术研究[D].西安：西安电子科技大学，2012：19-24.

[责任编辑：杨玉洁]