基于深度强化学习的配电网在线拓扑优化策略研究

胥 鹏，张 悦，王蓓蓓，朱 红，刘少君，许洪华

（1. 东南大学 电气工程学院，南京 210096；2. 国网江苏省电力有限公司 南京供电分公司，南京 210000）

0 引言

近年来，住宅、商业屋顶光伏系统以及兆瓦级光伏发电场的装机容量快速增长。DG 的高渗透性会导致在线电压频繁而大幅度地波动，并给工业生产带来安全问题和经济损失［1—3］。解决在线电压波动问题成为配电网面临的挑战之一。

传统的在线电压调节主要依赖于安装的设备。文献［2］中，智能逆变器和并联电容器被用来处理电压偏差，但只有前者用于在线调节。文献［4］采用半定松弛启发式算法对调压变压器分接头位置进行优化。文献［5］提出了用紧急需求响应处理光伏逆变器以达到调节上限时的在线电压问题。文献［6］提出了一种基于电压负荷灵敏度矩阵的电压控制分层需求响应策略。虽然需求响应技术发展迅速，但目前仍受通信延时、用户响应速度等因素影响，可在线调度的柔性负荷有限。在DG大幅波动的情况下，现有资源无法完全解决在线电压问题，而且盲目地增加新调压设备又是非常昂贵和浪费的。

拓扑作为一种电力系统调节方法，已被用于解决长时间尺度下的网损、电压优化等问题。近年来，智能电网中不同的智能终端设备使得电网拓扑能够灵活调节，进而处理在线电压问题。但获得最优的拓扑控制策略需要求解混合整数圆锥规划，因此这种基于优化的方法通常需要大量的计算时间。一些启发式算法例如粒子群优化算法（particle swarm optimization，PSO）［7］或遗传算法（genetic algorithm，GA）［8］，被用来解决这个问题。但这些启发式方法具有很强的优化随机性，容易导致局部最优解。由于这些限制，上述方法都不能满足在线拓扑优化（online topology optimization，OTO）的要求。

深度强化学习（deep reinforcement learning，DRL）是机器学习的一个理论分支，它使用数据驱动的方法，在动态环境中通过不断探索和尝试，找到高质量的解决方案［9—10］。在电压调节方面，DRL 方法一般被用于控制调压装置。但大多数现有的DRL 方法只关注于调整不同类型的调节装置，如智能逆变器［2］、电容器［4］、电池储能［11］等，或者尝试调用端侧需求响应资源。文献［12］中，当智能逆变器用完后，需求响应资源被用来作为调压资源的补充。文献［13］中，集群空调资源被用来与分布式光伏进行配合调压工作。需求响应资源参与调压时，一般根据其节点电压功率灵敏度矩阵得到需求响应调节量［6］。但目前已有的研究成果中很少考虑到灵活拓扑在电压控制中的潜力。

针对在线拓扑优化问题，本文基于DRL对其进行建模与求解，提出的DRL算法能够在数秒内得到合理的控制策略。此外，在IEEE 14 节点算例中验证了本文算法的有效性，相比于启发式或者经典优化方法，DRL 可以快速得到优质的拓扑方案，满足在线调压的需求。

1 重构问题数学建模

在这一节中，给出了在线拓扑优化问题的简单数学公式，包括目标和相关约束条件。

1.1 目标函数

对于在线拓扑调节，安全性和经济性可能是配电网运营商最关心的问题。目标函数为

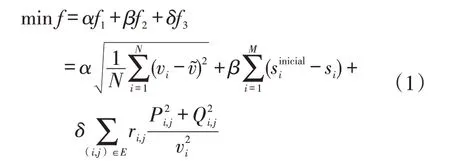
式中：f1、f2和f3分别为电压偏移量、开关次数和网损分量；α、β、δ分别为各分量的系数。具体来说，vi为总线i的电压幅值；si为表示开关i状态的二进制变量；对于E组中连接节点i和j的每条线路，Pi,j和Qi,j分别为相应的有功和无功功率；v͂为标准电压标么值，在不丧失一般性的情况下，设为1；为原始拓扑对应的开关状态；ri,j为线路阻扰。

1.2 约束条件

在线重构问题的基本约束条件是功率平衡约束，节点电压约束，线路电流约束和拓扑约束，具体如下

式中:Pi,Grid/Qi,Grid、Pi,Load/Qi,load、Pi,DG/Qi,DG分别为节点i变电站有功/无功注入、负荷有功/无功需求与DG 有功/无功出力；Vi、Vj分别为节点i和j的电压；Yi,j为网络的导纳矩阵；分别为节点i电压幅值上限和下限；Imaxi为支路i上允许流过的最大电流；Tr为放射性网络结构；Ii为线路i上的电流；G为配电网拓扑结构。

根据图论，网络结构保持放射性需要满足以下3个条件中的任意2个：

（1）闭合支路等于网络节点数减去变电站数

式中：Non为控制变量，表示闭合支路的个数；Nnode与Nsub分别为节点个数与变电站个数。

（2）网络图是连通的。

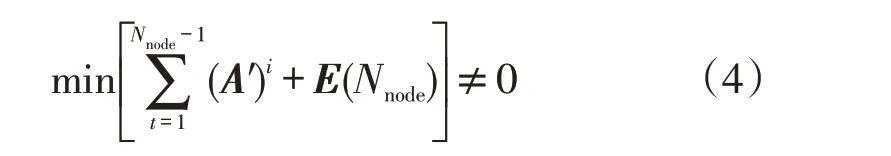
式中：E(Nnode)为Nnode阶单位矩阵；A′为网络邻接矩阵的转置矩阵。

（3）网络无环，不存在闭合回路。

2 DRL建模

本节基于DRL 对OTO 进行建模，对OTO 的状态、动作和奖励功能进行了建模。

2.1 深度Q网络

针对OTO问题中的离散变量，设计了一种基于深度Q网络（deep Q network，DQN）算法的DRL模型，该算法是目前应用较为广泛的DRL算法之一，自提出以来已经进行了多次改进。DQN实际上是Q-learning算法的一种升级，其基于Bellman方程［13］，通过更新动作值函数迭代确定最优策略。

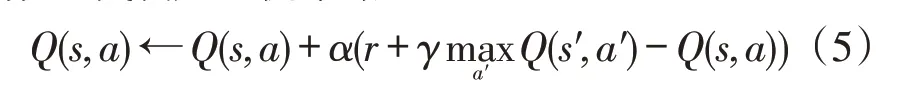
式中：Q(s,a)为状态-动作值函数；a、s、r分别为RL的动作、环境及奖励；s′、a′分别为新的环境与动作；γ、α分别为折扣与学习因子。然而Q-learning作为一种RL 算法，只能处理状态空间很小的问题。因此，DQN 提出深度Q 网络来起到函数逼近器的作用。网络的输入是状态，输出对应于所有动作的Q值。同时，为了降低Q(s,a)与Q(s′,a′)之间的相关性，引入了另一个深度网络，称为目标网络。每训练一定次数，将Q 网络的权值传递给目标网络。训练的损失函数可以表示为

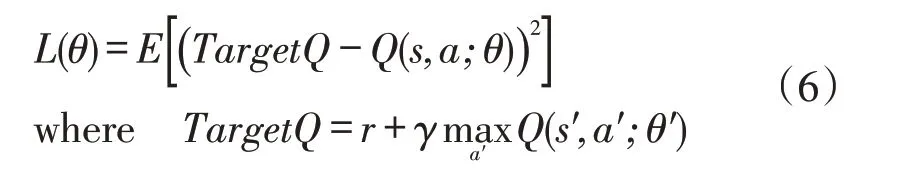
式中：θ′为深度网络参数。

DQN的另一个重要特性是经验回放，其中agent可以将其以前的经验存储为Q网络的训练样本。训练时，agent 随机抽取一定数量的样本，以避免相关问题。DQN 结构的具体说明如图1 所示。DQN 在训练过程中通过不断地迭代计算，使用随机梯度下降算法更新网络参数，以逼近目标网络。

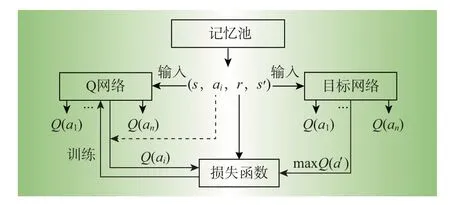
图1 DQN算法示意图Fig.1 Schematic diagram of DQN algorithm

2.2 状态定义

状态是智能体所处的外界环境信息，而环境状态的具体表现形式可以有很多种，例如多维数组、图像和视频等。外界环境的状态需要能够准确地描述外界环境，并尽可能地将有效信息包括在内，通常越充足的信息越有利于智能体学习。在OTO问题中，为了尽可能地将环境中的有效信息表达出来，同时考虑到日前优化中调用的调压资源，本文以并联电容器为代表。需要定义的状态具有如下形式

式中：G为当前配电网的拓扑结构，由节点元素V与边元素E构成；s为本文定义的状态；PLoad和QLoad分别为节点V上的有功和无功负荷；PDG为DG的有功出力；Qcap为电容器的无功调节。

2.3 动作定义

在OTO问题中，本文认为每条线路的状态都由一个馈线开关控制。馈线开关为1时，表示该条线路闭合；为0时，表示该条线路断开。DQN的控制对象包括配电网中所有的馈线开关，其动作维度为2M。随着网络规模增大，动作维度将出现组合爆炸。本文引入图论中的树枝交换理论，有效减小动作空间，加速DQN的学习效率。图论中的相关理论如下：

（1）树、树枝、连枝：对于连通图G，包含连通图的全部节点，但不含任何回路的连通子图t称为图G的树；树t上的边称为树枝；图G上非树t上的边称为连枝。

（2）基本割集（basic cut set，BCS）：t为连通图G中的一棵树；e为t的任一树枝；图G中仅包含t的一条树枝，其余均为连枝的割集叫做图G的基本割集；包含树枝e的基本割集记为Se(t)。

（3）树枝交换：t为节点数为N的图G中的一棵树。

若e∈t（即e为其任一树枝），支路b∈Se(t)，用b取代e后则可得到树t′，记为

若b≠e（即支路b是包括e的树t的基本割集中的连枝），那么t′≠t，意味着t′为新树；若b=e（即支路b是树枝e本身），那么t′=t。

重构问题中配电网的放射性约束即要求网络结构是一棵树，本文将DQN的动作设计为一次树枝的交换操作。具体来说，DRL从集合X中选择一条支路断开，并从该支路的基本割集中选择一条闭合，最终形成的拓扑必定满足放射性拓扑约束。

2.4 奖励定义

在DQN的建模中，对于奖励函数的设计没有固定的规律，往往需要根据实际问题具体分析，其在很大程度上影响DQN的学习方向与学习效率。本文奖励机制如表1所示。简单来说，当DQN选择动作后，会进一步从该动作的基本割集中按一定规则选择1条线路，若这条线路是其自身，则说明算法已经陷入局部最优，DQN会根据解的质量获得最终奖励rfinal，其大小由最终收敛拓扑所对应的目标值决定。目标函数f越小，得到的奖励将越大，因此，定义rfinal为

表1 机制1奖励机制Table 1 Incentive mechanism of mechanism 1

式中：f为式（1）中的目标函数；ω为其系数。

2.5 模型整体框架

在上述建模的基础上，本文对于OTO 问题的DQN算法流程如图2所示。根据配电网观测到的状态信息，DQN可根据不同动作的Q值选择要断开的线路，并计算该线路对应的基本割集。然后基于潮流计算从基本割集中选择1 条奖励最大的线路闭合，最终实现拓扑的一次操作。通过重复以上过程直到达到动作停止条件。

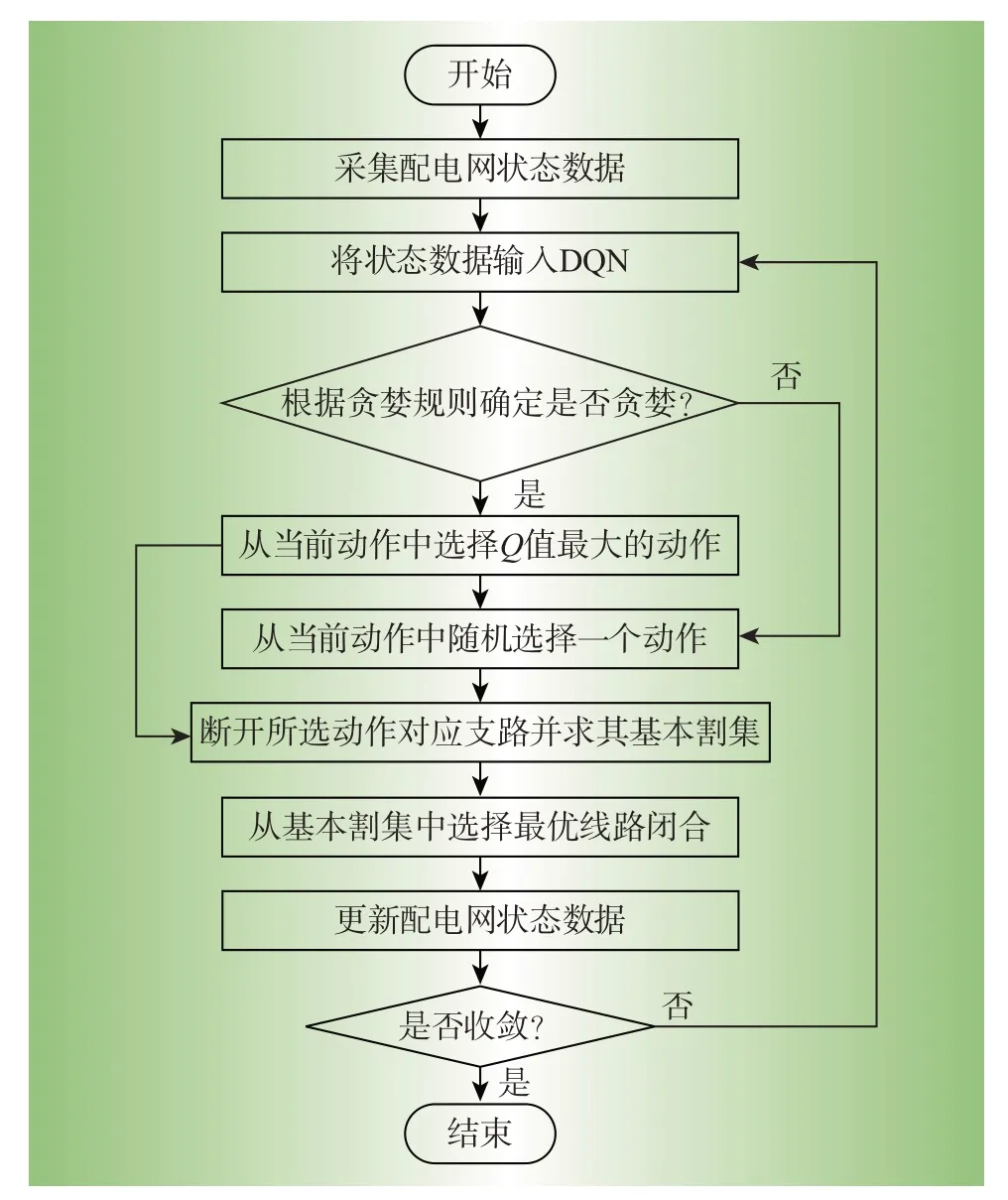
图2 算法流程图Fig.2 Algorithm flow chart

3 算例分析

本节以IEEE 标准14 节点网络为基础，进行多个方面的案例研究，以证明所提出方法的可行性和有效性。第3.1节详细说明了算例设置；第3.2节阐述了基于拓扑的电压控制的训练过程和测试结果；第3.3 节为了说明本文算法的优越性，进行了不同方法的对比分析。

3.1 算例设置

IEEE 14节点网络如图3所示，假设每段线路都有1 个智能开关，可以灵活地控制线路的状态。本文在节点2与节点7接入分布式新能源。负荷和风电数据的时间序列取自Pecan Street Dataport。该数据集包含几十个住宅客户和2 个风电场的数据，数据长度为1年，间隔为15 min。对于14 节点网络的每个节点，本文将随机10个用户的功率聚合为节点实际注入功率。所有节点的功率注入都通过1个转换因子进行调整以创建合理的负荷水平。

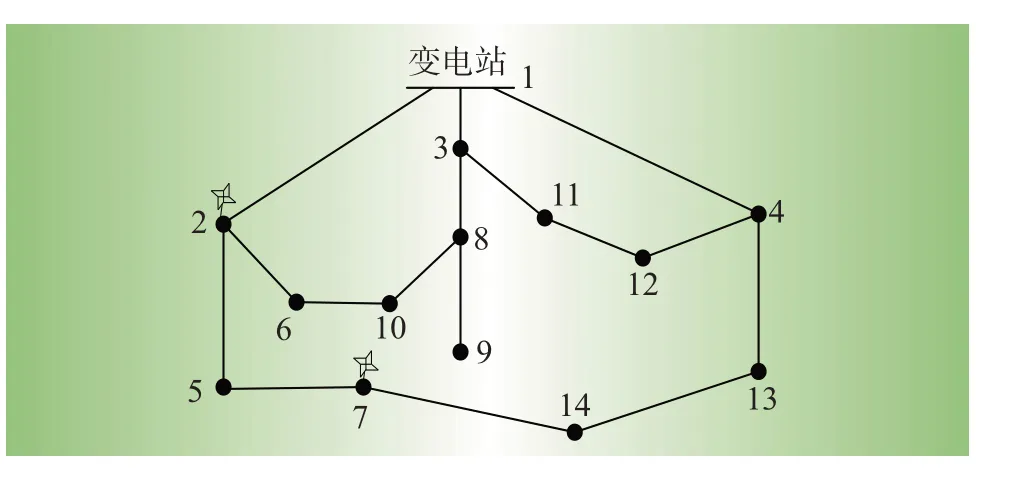
图3 IEEE 14节点示意图Fig.3 IEEE 14 node schematic diagram

其中转换因子β根据14 节点网络的标准负荷数据选择。另外，不同的拓扑数据由基于树枝交换操作的仿真得到。表2给出DQN的超参数设置。

表2 算法超参数设置Table 2 Algorithm super parameters setting

3.2 训练过程及测试结果

在这一部分中，首先给出训练过程的结果，然后利用基于数学优化算法求出的最优基准测试其有效性。

（1）训练过程：本文在每个训练集中学习200个样本，并计算其平均奖励。在训练了400集后，平均奖励的演变如图4 所示。在这个过程中，使用ε-greedy 策略帮助代理选择动作。在前95集的学习过程中，DQN 采取随机行动的概率从1.0 线性衰减到0.05。在接下来的305集里随机系数保持0.05不变。平均奖励在前95集以线性趋势迅速增加，然后振荡约100 集，最后从200 集开始稳定在2.7 左右。值得一提的是，虽热概率固定在0.95，但平均报酬仍有小幅波动。训练结果表明，所提出的基于DQN的方法可以逐渐学习到一个好的策略以获得大的奖励值，从而获得较大的拓扑调整回报。

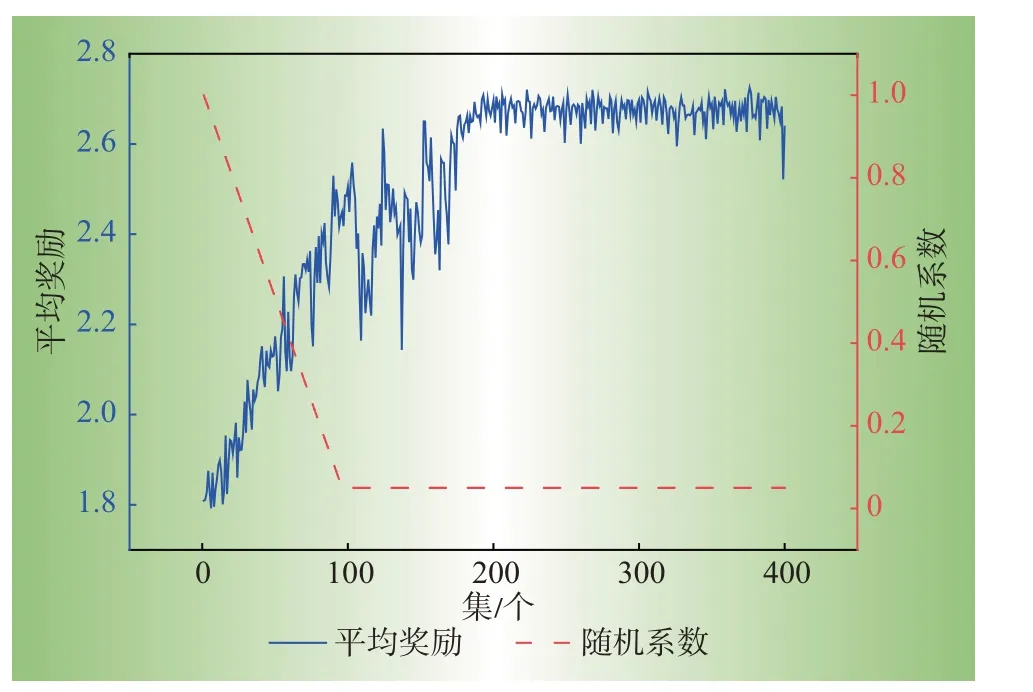
图4 平均奖励示意图Fig.4 Schematic diagram of average reward

（2）训练结果：为了检验DQN 模型在学习了400集之后，在不同样本下找到的拓扑方案的质量，本文利用CPLEX求解器求解混合整数规划问题，得到最优解，并将DQN的方案与对应样本的最优方案进行比较，如图5所示。

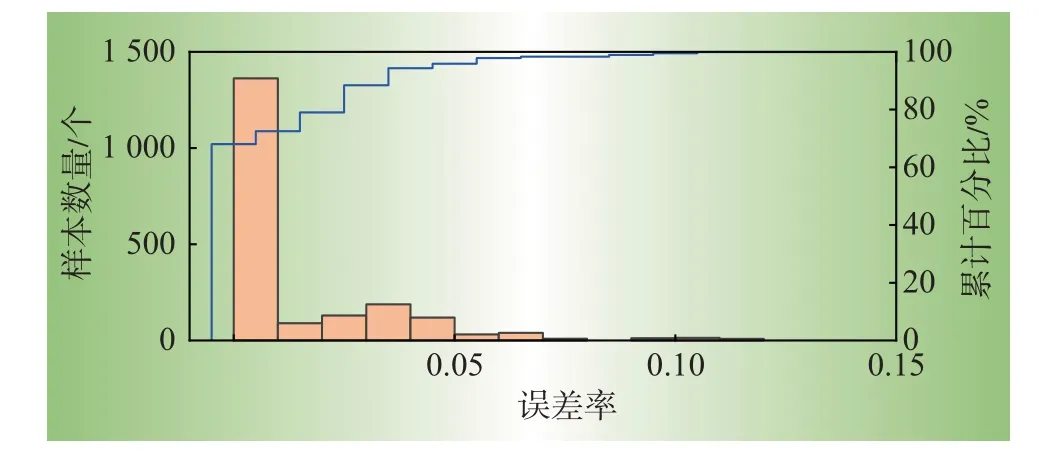
图5 DQN方案误差率分布图Fig.5 Error rate distribution of DQN scheme

DQN方法得到的结果与最优解相等，而对于其他大多数样本，该方法得到的结果接近最优解，说明了基于DQN的拓扑优化方法的有效性。同时，为了进一步评估DQN 模型的泛化能力，在400 个训练集后固定了DQN 参数，从测试集中随机选取100 个新样本进行测试，并将结果与最优解进行比较，如图6所示。对于智能体从未遇到过的大多数样本，DQN仍然可以立即给出最优或接近最优的策略。

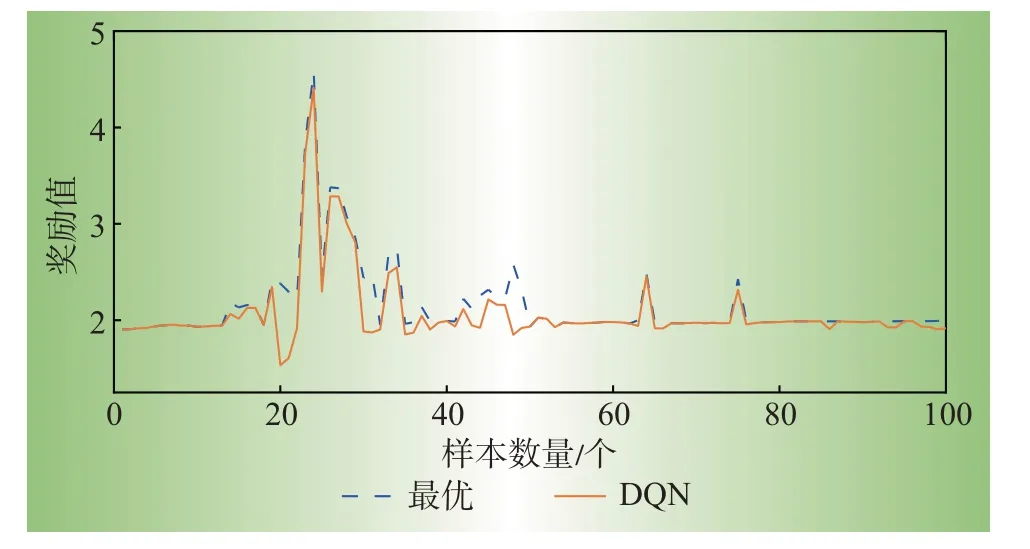
图6 DQN与最优方案结果对比Fig.6 Comparison between DQN and optimal solution

3.3 算法对比分析

为了评估提出的基于DQN的算法的性能，比较了其他几种求解方法，包括GA、PSO 和基于二阶锥的优化算法（mixed integer second-order cone programming，MISOCP）。GA和PSO都是求解拓扑优化问题的常用方法。目标函数与基于DQN 的方法相同，是使电压偏移量和网损最小。此外，基于二阶锥规划模型的商业求解器CPLEX-12.9 对1 个基于优化的MICP问题进行了求解。

基于每种算法对给定问题求解20次，并将求到的结果统计在表3中。相比于2种启发式算法，本文用DQN 方法求解20 次的结果更加贴近最优解。从计算时间来看，传统数学方法：二阶锥规划（secondorder cone programming，SOCP）所需要的时间远远大于其他3种方法。SOCP属于传统数学解析法求解，其所得解都是最优解，但其求解时间长也是数学解析法的固有问题，并且当问题规模变大后，求解时间会以指数级上升甚至使问题变得不可解。而PSO与GA 属于启发式求解方法，其求得的解是次优解，每次都可能不一样，但求解时间相比于SOCP 要短很多。PSO平均需要30.53 s，GA平均需要24.45 s。而本文DQN方法则都能在2 s内得到拓扑方案。这种速度的主要原因是SOCP 方法和启发式算法（包括PSO和GA）都不能使用先验知识。对于每个OTO问题，这些方法从一开始就寻找解决方案，这需要大量的计算时间。相比之下，DQN算法花费时间离线学习历史训练数据，并将学习到的信息保存在Q网络中。在处理在线问题时，本文提出的基于DQN的方法可以通过离线学习和保存的知识快速找到最优解。

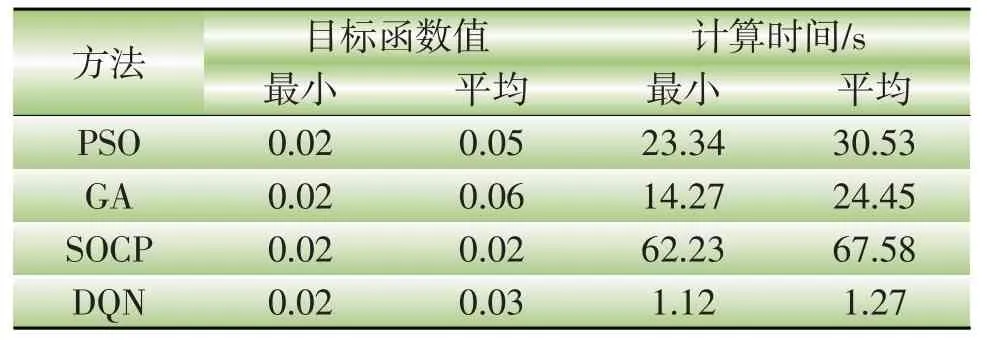
表3 不同方法求解结果Table 3 Solution results of different methods

4 结束语

本文提出了一种基于DQN 的OTO 问题求解算法。借助于所提出的DQN动作机制，减少了动作维度和动作空间。仿真结果表明，所提出的基于DQN的拓扑控制算法能够协调现有的调节资源，保证系统的安全性，并且DQN算法能够在数秒内处理OTO问题，给出合理的解决方案，并可与配电网中的现有资源协调处理在线电压问题。