基于图连通支配集的子图匹配优化算法

孙云浩 韩 冰 李冠宇 邢维康 李逢雨(大连海事大学信息科学技术学院 辽宁 大连 116026)

0 引 言

模式匹配是一个子图同构问题，给定一个查询图和数据图，模式匹配是指搜索到所有同构于查询图的数据子图[1]。基于节点的子图匹配方法是解决模式匹配问题的一种有效方法，其以节点作为最小匹配单位，利用了SSR(State Space Representation)树模型构建模式匹配的执行过程[2]。其中，状态表示一个由查询图节点和数据图节点组成的节点对。如果查询图节点和数据图节点满足匹配条件(查询图节点出度小于数据图节点出度，查询图节点入度小于数据图节点入度，查询图节点标签与数据图标签相同等)，则将其加入SSR树模型。当匹配成功的节点数量等价于查询图节点数量，则输出一个子图匹配的答案集。

基于节点的子图匹配算法主要通过优化节点匹配可行性规则、匹配的执行序列和搜索空间三方面提高算法的执行时间效率。最早的算法思想是由Ullmann[4]提出，其主要通过比对查询图节点和数据图节点的度的大小来过滤数据图节点。然而，这种过滤手段是粗糙的，其过滤后的候选数据图节点过于庞大。VF2算法[5-6]在缩减候选数据图节点方面贡献突出，其通过添加邻接节点的可行性规则来缩减候选数据图节点的规模。然而，其匹配的执行序列是随机的，忽略了执行序列对时间效率的影响，导致处理大规模数据时，查询时间过高。文献[5]提出了GADDI算法，定义了邻近辨别子结构距离(NDS)，表示两个节点及相邻节点结构中频繁子图的数量，通过约束模式图中节点的NDS距离来过滤备选节点。文献[6]提出的Spath算法引入更复杂的邻接结构，提出了以节点之间的最短路径作为匹配最小单位，定义了以节点为中心，采用层次遍历的三元组表示方法，通过更加复杂的结构和语义信息，提高筛选候选节点的能力。VF3[2]算法是针对大规模稠密的数据图，其通过一种动态的代价计算模型，最大程度上兼顾了匹配序列的局部和全局优化，其次，通过查询图的节点标签对数据图节点分类，从而进一步缩减搜索空间的规模。VF3利用动态代价计算模型试图编排最优的执行序列，然而最大回溯深度仍然等价于查询图节点的数量，其整个匹配过程中的迭代次数没有得到真正意义的降低。

因此，本文提出一种基于图连通支配集的子图匹配优化算法，其主要思想是通过查询图支配节点降低查询节点在搜索过程中的迭代次数，即降低搜索空间的大小。

本文主要贡献如下：给出查询图节点的最小连通支配集求解模型，构造代价模型，编排最小连通支配集匹配序列，利用支配节点的结构信息对搜索空间进行有效剪枝，通过实验评估得出本文方法比其他同类算法具有更高的时间效率。

1 查询图节点重要度

1.1 节点匹配算法思想

节点匹配算法是一种回溯算法，其算法思想主要包括三个部分：(1) 利用查询图节点的出度(查询图节点的出度邻接节点称之为后继节点)和入度(查询图节点的入度邻接节点称之为前驱节点)保障查询节点匹配的连续性；(2) 通过优化策略来优化查询图节点的执行序列；(3) 利用有效的剪枝规则降低搜索空间的大小。

节点匹配的过程可以看作顺序执行的过程，依次激活查询图的节点并获取当前查询节点在数据图中的候选集。一个查询节点u的候选集是指数据图中可以与u匹配的数据节点的集合。如果查询节点与当前所有候选数据节点匹配失败，需要回溯到上一查询节点，匹配上一个查询节点其他候选节点。其搜索空间可以用树形结构表示。树的根节点为空，其他节点为查询图节点与其匹配的数据图节点组成的节点对。如果查询图节点的数量为n，那么树结构中任意一条从根节点到第n层节点的路径中的数据图节点可以构成查询图的一个答案集。

如图1所示，图1(a)给出一个查询图，其为一个带标签的有向图。查询图Q包括10个查询节点(u0,u1,…,u10)并标注了相应的节点标签(A,B,…,J)。图1(b)给出一个数据图，其图结构的描述与查询图类似。不同之处在于查询图规模远远小于数据图规模。

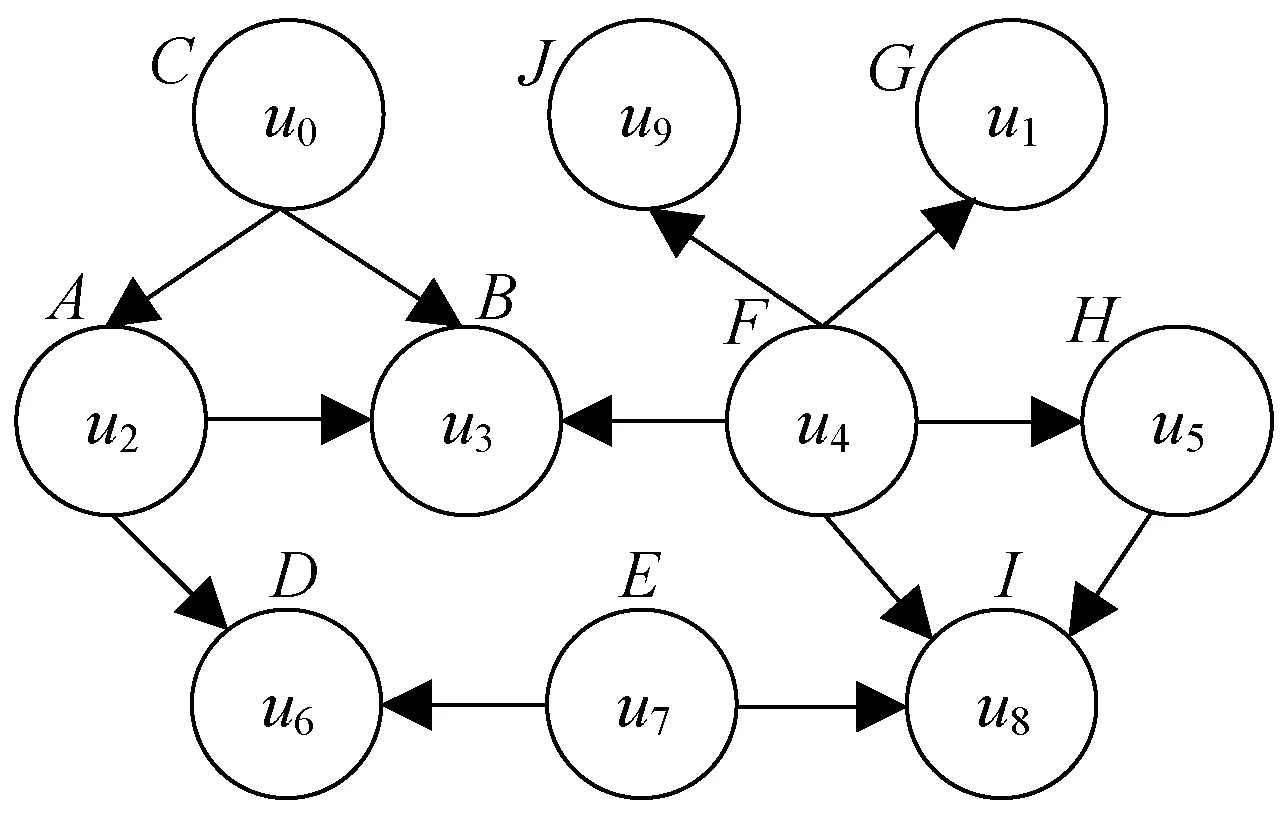
(a) 查询图

已知在给定的查询图(图1(a))中，节点个数为10，节点的匹配执行顺序有10!种。例如：是查询图的一个匹配序列，匹配到第4层，即获取节点u6的候选节点，匹配次数达到10×100×1×10次，以的匹配序列，匹配到第四层匹配次数为1×10+10+2次。原因是查询图中节点u0在数据图中候选集个数为100(节点v11到v111)，在匹配序列中需要回溯100次，导致查询次数增多。由此可以得出结论，节点匹配顺序的不同会导致迭代次数不同，进而影响查询效率。因此，本文重点在如何降低迭代次数以提高查询效率。

1.2 问题定义

查询图和数据图可以形式化定义为(V,E,L)，其中：V指代的是一个有限的节点集合，E是一个有向边的集合，L指代的是节点标签。是由vi指向vj的边。本文形式化定义查询图(如图1(a)所示)和数据图(如图1(b)所示)为Q(VQ,EQ,LQ)和G(VG,EG,LG)。

定义1子图匹配。给定一个查询图Q(VQ,EQ,LQ)和一个数据图G(VG,EG,LG)，子图匹配定义为从Q和G之间的一个映射函数f:VQ→VG,满足以下条件，称Q和G满足子图匹配。

∀u,v∈VQ(u,v)∈EQ→(f(u),f(v))∈EG

(1)

LQ(u)=LG(f(u))LQ(v)=LG(f(v))

(2)

式中：L(u)表示节点标签。

定义2查询节点匹配序列。给定查询图Q(VQ,EQ,LQ)，查询图节点匹配序列被定义为一个序列sn=，满足∀ui∈V(sn),∃uj∈V(si-1)，使得uj∈adj(ui)。adj(ui)为ui的邻接节点集合。

定义3k查询节点匹配序列。给定一个查询图Q并获得一条Q的全节点匹配序列sn=。k查询节点匹配序列指的是全节点匹配序列sn的子序列sk=，1≤k≤n，满足以下条件：∀ui∈V(sn)-V(sk),∃uj∈V(sk)，使得uj∈adj(ui)。

获取k查询节点匹配序列是本文要解决的第一个问题，通过获取k查询节点来减小N，提高查询效率；构造代价模型选取具有较好区分度节点，优化k查询节点匹配序列是本文要解决的第二个问题；利用节点结构特征减少节点候选集的数量是本文要解决的第三个问题。

2 基于支配节点的子图匹配

基于图连通支配集的子图匹配方法主要包括三个步骤：(1) 通过贪心算法获取查询图的最小连通支配子图(NP难问题)，构造k查询节点匹配序列；(2) 优化k查询节点匹配序列；(3) 利用支配节点结构特征对搜索空间剪枝。

2.1 支配集及最小支配集

对于查询节点ui，其候选节点集为C(ui)。如果节点uj为节点ui的邻接节点，那么uj的匹配节点一定包含在C(ui)的邻接节点中。因此，已知节点ui的匹配节点，很容易搜寻到节点uj的匹配节点，可以称节点ui支配节点uj。基于上述论证，本文利用节点之间的支配关系，缩小全节点匹配序列的长度，构造k查询节点匹配序列。节点之间的支配关系是源自于支配集的概念，因此首先介绍与节点支配集[9-13]以及支配子图的相关定义。

定义4节点支配集。给定一个查询图Q(VQ,EQ,LQ)，节点支配集DS⊆VQ满足：∀u∈(VQ-DS)，∃v∈DS，使得u与v存在一条边，那么，u是v的被支配节点，或者说v是u的支配节点。

查询图中除节点支配集，剩余节点集合称为被支配集，记作NDS。图2给出了图1查询图可能存在支配节点及其被支配节点。由节点支配集定义可知，在支配集中，任意两个支配节点之间边的数量可能为1、2、3，即支配集中任意两个支配节点之间边的数量小于等于3。

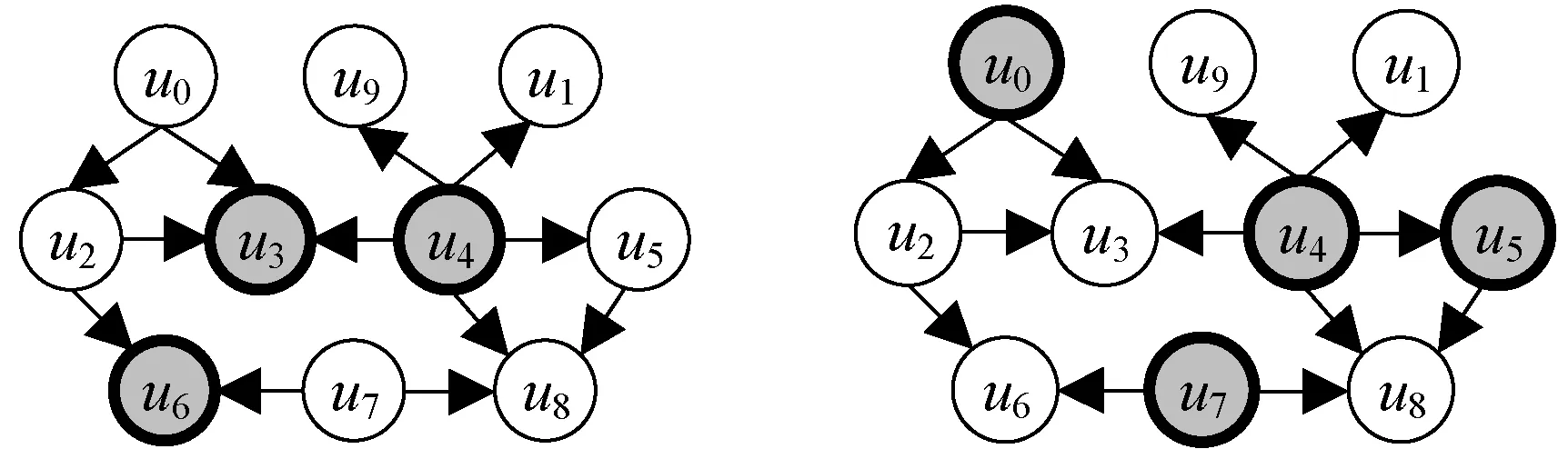
(a) (b)

(c) (d)图2 支配节点以及被支配节点举例(阴影为支配节点)

定理1节点支配集定理。给定图G，集合DS为G的支配集，满足：(1)DS⊆VQ,(2)∀u∈VG→u∈DS∨u∈adj(v)(v∈DS)。

证明：假设存在一个节点u既不属于集合DS又不属于集合DS中某些节点的邻居节点，则一定会出现以下情形：存在两个支配节点之间的边的数量大于3，与节点支配集定义相矛盾，因此定理1成立。

由支配集节点构成的子图称之为支配子图，记作QD，图3给出图2(c)的支配子图。由图2可知，给定一个查询图，查询图中可能存在多种不同的支配集，如(u0,u4,u5,u7)、(u3,u4,u6)、(u2,u3,u4,u6)、(u3,u4,u7)。在图2给出的支配集中，由图2(a)、(b)、(d)的支配集构成的支配子图是非连通的。依据k查询节点匹配序列定义，节点之间满足连通性。要在保证连通性的前提下寻找最小支配子图，即保证连通性条件下使得支配集中节点个数尽可能地少。文献[8]证明：任意一个节点个数为n的图模型，其支配子图数目的最小值和最大值是1.570 4n和1.715 9n。而找出最小支配子图是一个NP难问题，在已有的方法中，最快的精确查找最小支配子图算法时间复杂度为O(1.495 7n)。文献[9]提出一种贪心算法来找出近似最小支配集，但是在该方法得到支配集在查询图上是非连通的，即支配集节点之间可能不存在边关系。综合考虑，本文在此基础上进行改进，提出一种基于贪心搜索近似最小连通支配子图算法。

定理2邻接定理。假设查询图Q是数据图G中的一个子图匹配。图XD是支配子图QD的一个子图匹配(XD⊆G,QD⊆Q)。∃ui∈QD,uj∈Q，∈E(Q),一定存在节点vi=f(ui),vi∈XD,vj=f(uj),vj∈G,满足:∈E(G)。

证明：假设节点ui的匹配节点为vi，且ui存在一个被支配节点um，在节点vi的被支配节点集搜索不到节点um的匹配节点。不满足定义1中式(1)，因此节点vi不是节点ui的匹配节点，与假设节点vi是节点ui的匹配节点相矛盾，因此定理2成立。

定理2说明如果节点ui是支配节点，vi是ui的匹配节点，um是ui的被支配节点，那么um的匹配节点属于vi的被支配节点。

定理3k查询节点匹配序列不失完整性。由k查询节点匹配序列得到子图匹配，记作G(k)，由全查询节点匹配序列得到子图匹配，记作G(n)。G(n)⊆G(k)。

证明：由k查询节点匹配序列定义知k查询节点匹配序列指的是全节点匹配序列s的子序列sk=,1≤k≤n，即sk⊆sn。因此满足全查询节点匹配序列的子图匹配必然满足k查询节点匹配序列。

由定理3可知，由k查询节点匹配序列搜索得到的子图匹配包含查询图的所有子图匹配，证明利用k查询节点匹配序列在降低了搜索空间大小的前提下，可以匹配到所有答案集。

2.2 最小连通支配子图

本节主要对于最小连通支配子图的查找做出详细论述。文献[9]采用贪心的方法来查找最小支配集，找到的最小支配集是非连通的。与本文问题定义不一致，因此本文对该方法进行改进，提出一种新的基于贪心搜索最小连通支配子图算法。本节首先介绍最小连通支配子图的概念，然后介绍如何寻找最小连通支配子图。

定义5连通支配集。给定一个查询图Q(VQ,EQ,LQ)，节点支配集DS中，如果节点在图Q上是连通，就称为连通支配集，记作CDS。支配节点数最小的连通支配集称为最小连通支配集，记作MCDS。

定义6最小连通支配子图。图Q的所有支配子图中，节点数目|V(QD)|最少且节点在图Q上是连通的支配子图称为Q的最小连通支配子图，记作QMCD。

算法开始时，初始化支配集合MCDS=∅，M=V(Q)(表示查询图中所有节点)，不断向集合MCDS中加入节点，删除集合M中度最小的非支配节点，直到M=MCDS。在算法1中查询图中的节点分为两类：一类是支配节点，记作MCDS；另一类是非支配节点M。算法的基本思想是对于给定的查询图在保证图连通的前提下，不断删减M集合中度最小的非支配节点。为了保证图的连通性，在删除节点时需要判断其邻接节点中是否存在度为1的节点；如果存在，则将该节点标记为支配节点，加入集合MCDS。

算法1FindMCDS-Graph

输入：查询图Q。

输出：最小连通支配子图QMCD。

1.function FindMCDS-Graph(Q){

2.setMCDS=∅,M=V(Q)

3.while(∃v={v|v∈M∧v∉MCDS}){

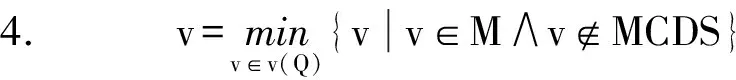
5.Q=M-v;

6.if(alld(N(v))>1){

7.M=Q;

8.if(∃N(v)∈MCDS){continue};

10.MCDS=MCDS∪u;

11.else{

12.MCDS=MCDS∪v;

13.}

14.FindE(QMCD) based onMCDS

15.returnQMCD;

16.}

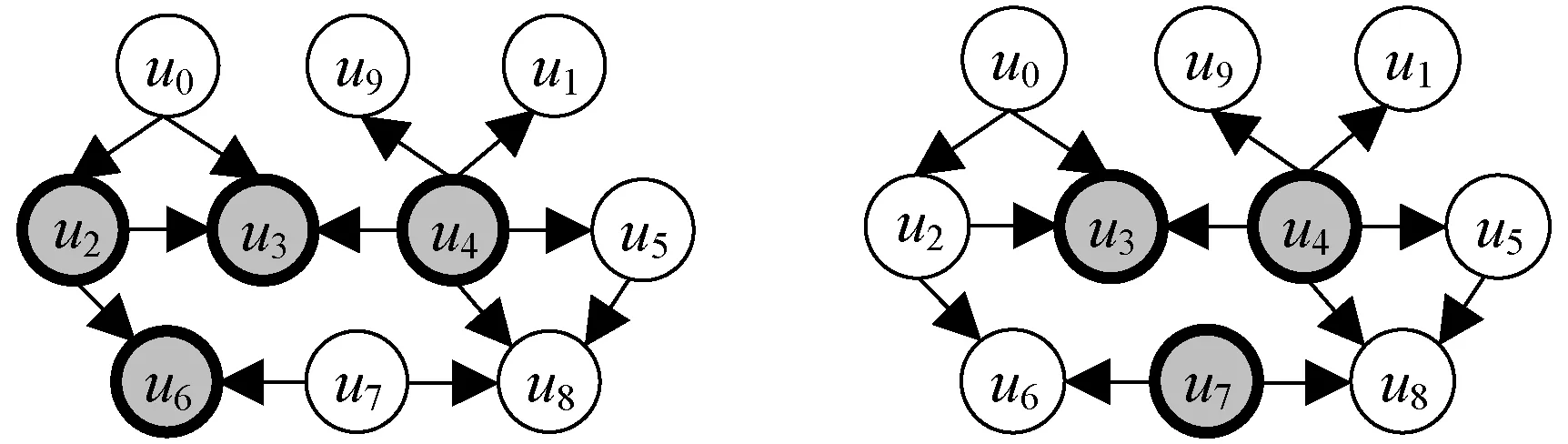
按照算法1，需要不断从查询图中删除节点，直到再删除其中任何一个节点都会破坏其连通性。图1(a)中查询图的最小连通支配子图过程是：初始化MCDS=∅，M=V(Q)；根据查询图中节点度的大小降序排序得到节点u1且该节点不存在度为1的邻接点，执行第9行，找到节点u1邻接点中度最大的节点u4。节点u4加入支配集MCDS中(图4(a))；节点u9的邻居节点u4为支配集节点，因此节点u9可以直接删除(图4(b),算法第8行)；继续执行下一个循环，选择下一个度最小的节点，此时节点u0、u5的度数均为2，假设选择节点u5。节点u5不存在度为1的邻接点，且节点v5的邻接点v4属于支配节点，所以可以判断节点u5是非支配节点，可以直接删除(图4(c))。依次类推，节点u8直接删除(图4(d))，节点u7的支配节点为u6(图4(e))，此时MCDS={u4,u6},M={u0,u2,u3,u4,u6}，需要删除节点u0，其邻居节点为u2、u3。如果将节点u2置为支配节点，M集合中只有节点u3不属于支配集MCDS，但节点u3存在度为1的邻接点u4(第6行)，节点u3不能被删除。将节点u3加入支配集MCDS(图4(f))。至此，M集合中不存在任何一个非支配节点(MCDS=M)，最终最小连通支配集为MCDS={u2,u3,u4,u6}。图3给出的支配子图为最小连通支配子图，其存在不同的节点匹配序列，如、。由于查询节点的出度入度大小不同，节点标签不同，导致在数据图中候选节点个数不同，因此查询节点不同的执行顺序会造成查询响应时间的不同。下节将详细介绍如何选取最优k查询节点匹配序列，提高查询响应效率。

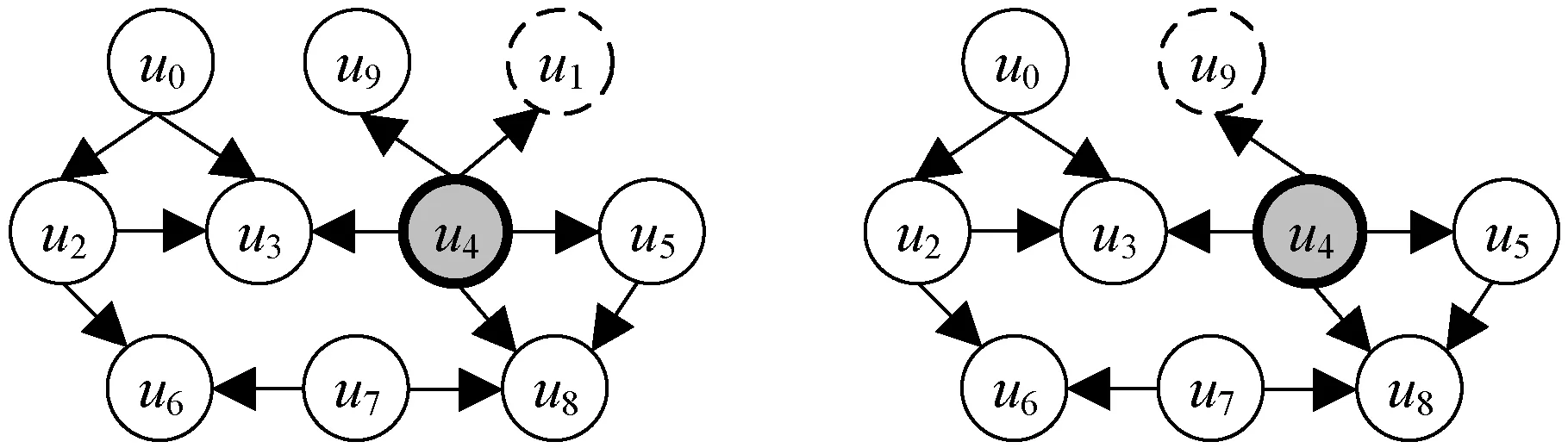
(a) 删除节点u1，标记支配节点u4 (b) 删除节点u9

(c) 删除节点u5 (d) 删除节点u8

2.3 最优k查询节点路径

1.1节举例说明了查询节点的匹配顺序影响子图匹配的效率。因此，通过优先选择区分度高的节点，快速确定第一个查询节点的答案集并以此缩小其他查询节点的搜索范围，提高查询速度，其核心在于查询节点的处理顺序。本文修改了文献[14]提出的代价模型，通过对数据图与查询图节点标签，节点度的大小及节点间结构信息进行代价分析，设计成本模型。其模型函数如下：

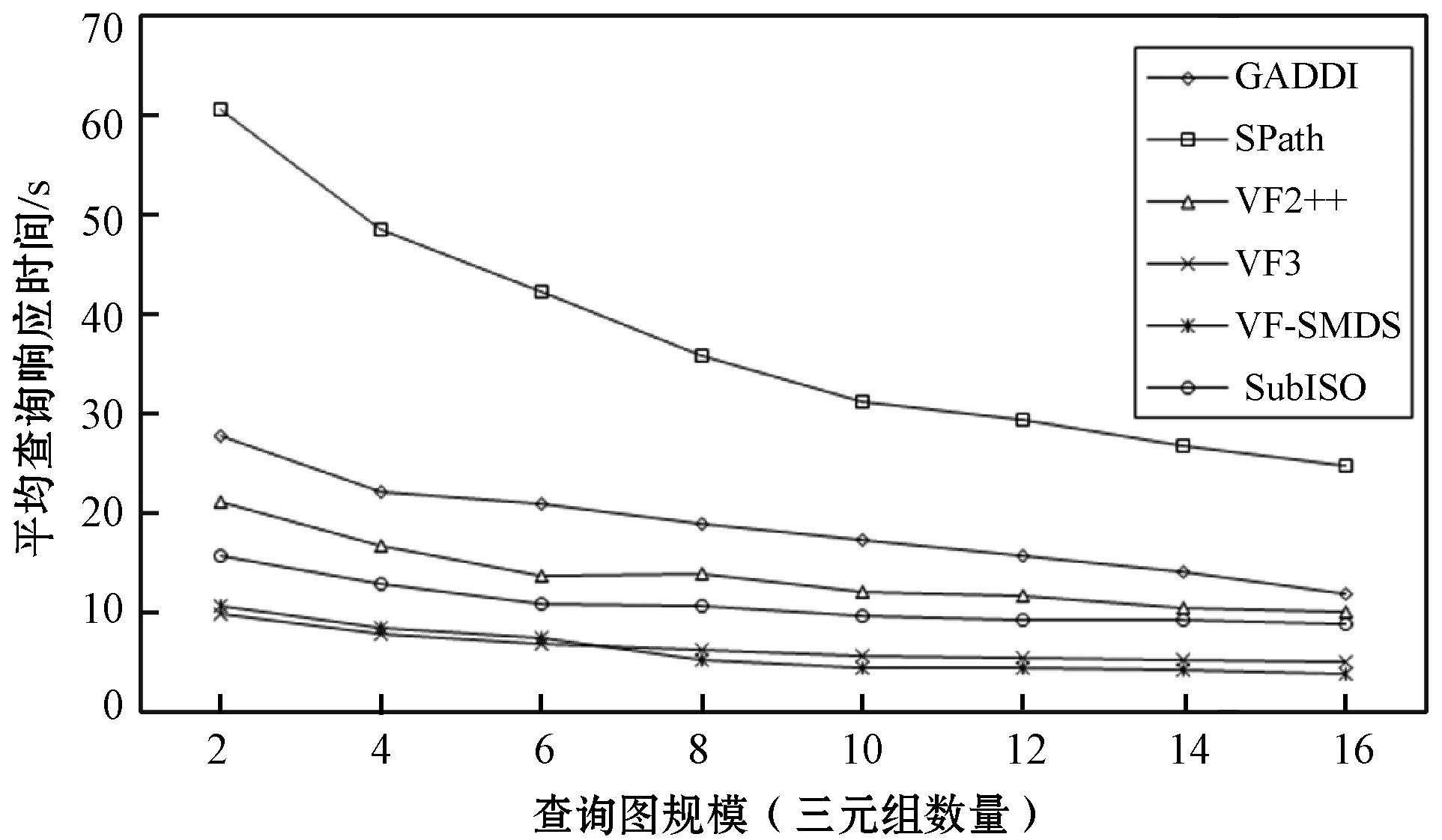
N(ui)=|E(ui,uj)|(0≤j

(3)

W(u)=NG(u)/|deg(u)|

(4)

NG(u)=|{LG(u)|LG(u)∈G}|

(5)

式中：函数N(ui)匹配序列中第i个节点与前i-1个节点之间的边的数量；|deg(u)|代表节点u的度的大小；函数NG(u)表示查询图节点u候选节点个数。成本模型遵循以下规则：

(1)N(ui)的值越大代表节点ui与已匹配节点存在边数量越多，受约束越大，候选集越少，匹配代价越低。如果N(ui)相同，遵循规则(2)。

(2)NG(u)越小，|deg(u)|越大，W(u)则越小，表示节点u在数据图中的候选节点越少，所支配的节点个数越多。

表1给出了查询图支配节点成本模型的计算值，基于此可以初步确定k查询节点匹配序列为。需要注意的是，最小连通支配子图的任意一个节点一定与图中某一节点存在至少一条边关系，如果当前节点与已匹配成功节点之间有尽可能多的边关系，可以减少当前节点的搜索空间。因此，确定节点顺序过程中，优先考虑N(ui)值。对于初始节点N(ui)的值均为0，选取W(u)值最小的节点u2。按成本模型计算，此时剩余节点中N(u3)=1、N(u6)=1、N(u4)=0、W(u3)=10、W(u6)=50,所以k查询节点路径中第2个节点为u6。依次类推，此时剩余节点中N(u3)=1，N(u4)=0，k查询节点路径中第3个节点为u3。因此，查询图的全节点路径顺序为。

本节重点阐述通过选择区分度高、候选集少的节点进行优先匹配来提高匹配效率。除此之外，通过有效的剪枝规则减少候选节点的数量也是降低查询响应时间的重要因素。

2.4 剪枝策略

由定义4可知，支配节点的被支配节点，均为该节点的邻接节点。图1(a)中，节点v133的被支配集NDS(v133)={v10,v256,v357,v234}。同理，对于图1(b)中查询图中节点u4的支配集NDS(u4)={u3,u9,u5,u1,u8}。

搜寻查询节点的候选节点，基本方法是利用节点标签及度的大小，例如在图1中C(u4)={v123,v124,…,v133}。把查询图转化为由支配节点构成的最小连通支配子图，保存节点的邻接节点时间复杂度为O(1)，因此可以通过保存支配节点结构特征，利用支配节点的结构特征对搜索空间进行剪枝。

定义7被支配节点标签集合。给定数据图G,节点v∈V(G),节点标签l∈L。被支配节点标签l集合NDLSl(v)的定义如下：NDLSl(v)={u|u∈NDS(v),L(u)=l}。

NDLSl(v)表示由节点v的被支配节点中标签为l的节点构成的集合。被支配节点标签集合NDLS(v)={NDLSl(v)|l∈L}，表示NDLSl(v)的集合。

在图1(a)中，数据图中节点v133的被支配节点标签集合NDLS(v133)={{v10:B},{v256:J},{v357:H},{v234:G}}，同理，对于图1(b)中查询图中节点u4的被支配节点标签集NDLS(u4)={{u3:B},{u9:J},{u5:H},{u1:G},{u8:I}}。

定义8候选约束。给定节点u∈V(Q),v∈V(G),如果，l∈L,都满足|NDLSl(u)|≤|NDLSl(v)|,则称NDLS(u)受约束于NDLS(v)，记作NDLS(u)▷NDLS(v)。

定理4给定数据图G和查询图Q，如果G中存在Q的一个子图匹配，即Q⊆G，那么∀u∈V(Q),NDSQ(u)▷NDSG(f(u)),f(u)∈V(G)。

证明：给定数据图G查询图Q,已知G中存在Q的一个子图匹配(Q⊆G)，则会出现以下情形：

(1) |V(Q)|=|V(G)|,|E(Q)|=|E(G)|时，Q中边的数量与G中边的数量相同，此时Q中任意支配节点的被支配节点数量等于G。∀u∈Q,v=f(u),|NDLSl(u)|=|NDLSl(v)|。

(2) |V(Q)|<|V(G)|,|E(Q)|<|E(G)|时，Q中节点和边的数量均小于G的数量，且Q⊆G，∀u∈Q,u′=f(u)(u′∈G),均满足∀v∈NDS(u),∃m∈NDS(u′)且m=f(v)，|NDLSl(u)|≤|NDLSl(v)|。

综上所述，定理4成立。

由定理4，节点u∈V(Q),v∈V(G)且v∈C(u)，如果|NDLSl(u)|>|NDLSl(v)|，则证明节点v并非正确候选集，可以从节点v的候选集C(u)中删除，来降低搜索空间大小。例如，在图1给出的数据图和查询图中，节点v133∈C(u4),是节点u4的候选节点，但是由于|NDLSi(u4)|=1，|NDLSi(v133)|=0，|NDLSi(u4)|>|NDLSi(v133)|，不满足定理4，节点v133非正确候选集，可以将节点从集合C(u4)中删除，以此减少搜索空间。

k查询节点匹配序列执行完成后，继而搜索剩余节点(非支配节点)的匹配节点。剩余节点的候选节点均为k查询节点匹配序列中节点(支配节点)的邻接节点。由定理2可知，通过支配节点的匹配节点可以搜索到非支配节点的候选集。例如：被支配节点u0存在2个支配节点，分别为支配节点u2和支配节点u3。易分析，被支配节点u0的候选节点需要同时为节点u2和节点u3匹配节点的被支配节点，因此可得节点u0的候选集节点:C(u0)={adj(C(u2))∩adj(C(u3))∩C(u0)}。adj(C(u2)),adj(C(u3))分别表示节点u2、u3的候选节点的一阶邻居节点，其中adj(C(u2))={v1,v2,…,v122},adj(C(u3))={v11,v111,v123,…,v133}，C(u0)={v1,v2,…,v111}。节点u0的候选集为C(u0)={v11,v111}，缩小了被支配节点候选集的大小。

3 实 验

3.1 实验环境与数据集设置

近年来，模式匹配技术在学术界获得越来越多的关注，研究机构发布了许多评测数据集。数据集主要分为真实数据图数据集、合成数据图数据集。本文实验采用AIDS Antiviral数据集[15-16]、Yeast数据集[17-18]、YAGO2数据集[19]。AIDS Antiviral数据集主要包含结构稀疏的无向图，每幅图表示一种化学物质的原子结构，原始数据来源于发展治疗项目。Yeast数据集包含一个唯一大图，边12 519条，节点3 112个。图中每个节点代表一种蛋白质，边代表两个蛋白质之间的作用关系，Yeast数据集中节点的度大小平均为8.05。与AIDS Antiviral数据集相比，该数据集的图更加稠密。YAGO2数据集包含一个唯一大图，边86 282条，节点4 675个，图中每个节点的度平均为36.82。相比于Yeast数据集，规模更大结构更加稠密。数据集详细信息如表2所示。

将本文方法与模式匹配代表算法(GADDI、SPath)，以及近几年的算法(VF2++[20]、VF3、SubISO[21])进行比较,测试的代码以及相应的数据来源于文献[2,15,20-21]。Ullmann和VF2算法是基础的模式匹配的算法，后续改进算法在性能上已远远超过原始算法，本文不再对Ullmann和VF2的性能进行比较。本文一共做了三组对比实验，分别从数据库构建时间、存储空间和查询响应时间三个方面对算法的性能进行分析。

本实验设备采用Windows 10 64位系统，CPU：Intel(R)Core(TM)i7-7700U CPU@3.6 GHz,内存：16 GB。

3.2 实验分析

实验一分析了数据集构建时间。表3中给出了GADDI、SPath、VF2++、VF3、SubISO、VF-SMDS算法在AIDS、Yeast、YAGO2数据集上数据库构建时间的比较。由表3可见，在构建数据库过程中，VF2++、VF3、VF-SMDS在三个数据集上的数据库构建时间相差较小，与其他三种算法相比所需时间比较短，这是因为VF2++、VF3对数据图无须提取辅助结构，预处理所需时间短。VF-SMDS需要保存节点邻接结构信息。SPath需要计算并保存k阶邻居结构。SubISO算法需要预先计算节点偏心率(节点间最短路径的最大值)，GADDI需要预先计算NDS距离，所以数据库构建的时间与其他三种算法相比最长。

实验二分析了数据集存储空间。表4是不同算法在三种数据集上的存储空间的比较。由于Spath引入了复杂的邻接信息，以节点为中心采用层次遍历的三元组表示方法，因此除了数据图节点还需要额外存储节点的k阶邻接信息，Spath的存储空间是VF-SMDS的2.1～5.0倍。而GADDI则需要存储两个节点及相邻节点的NDS距离，SubISO需要存储节点偏心率，存储空间是VF-SMDS的1.2～2.1倍。VF2++、VF3存储空间略低于VF-SMDS，因为VF-SMDS更好的利用邻接节点的结构信息来降低查询响应时间。

查询图中三元组的数量范围区间为[3，15](查询图中三元组的数量表示查询图的规模)。在AIDS、Yeast和YAGO2数据集中，查询图规模小于6时，查询图结构较为简单，只有在查询图规模大于等于6时，才会出现复杂结构。

实验三分析了算法的平均查询响应时间。图5给出以上六种算法在三种数据集上针对不同规模的查询图进行子图匹配的平均查询响应时间。在AIDS数据集上，VF3匹配速度最快，VF-SMDS、SubISO、VF2++、GADDI、SPath的平均查询响应时间分别是VF3的1.06倍、1.7倍、2.1倍、2.8倍、6.1倍。SPath平均查询响应时间最高主要在于筛选备选节点时，需要匹配节点周围大量的邻接节点。GADDI算法在匹配过程中需要计算查询图中任意两个节点间的DNS距离，导致过高的时间复杂度；此外AIDS数据集结构稀疏，存在大量DNS距离为0，降低了GADDI算法筛选备用节点的能力。VF2++和VF3算法的优化策略分为两步：确定节点匹配顺序，缩小候选集大小。但是VF2++算法确定节点匹配顺序仅考虑到了节点的标签及度的大小，过滤效果比VF3算法差。SubISO算法通过比较查询图节点与候选节点的偏心率来缩小数据图候选区域规模，AINDS多为规模较小数据图，导致SubISO筛选效果较差。Yeast数据集上，数据集的稠密度增大，GADDI、SPath、VF2++分别在查询图规模大于7、9、9时出现指数级的匹配时间，而VF3、SubISO和VF-SMDS查询响应时间上升趋势远远小于GADDI和SPath，这主要是因为SPath需要计算节点周围标签路径及对标签路径合并，导致大规模图查询响应时间高；GADDI缺乏有效节点合并顺序。VF2++算法过滤候选集时，仅考虑节点标签以及度的大小，导致搜索空间过大，回溯次数较多，查询时间过长。在YAGO2数据集上，GADDI、SPath、VF2++、SubISO、VF3算法在查询图规模分别为5、7、7、9、11时表现出指数级别的匹配时间。YAGO2数据集结构更为稠密，随着查询图规模的增大，查询图的结构更为繁琐，VF3算法未充分考虑查询图的结构信息，在查询过程中回溯次数过高，导致平均查询时间的上升。而SubISO算法虽然缩小了数据图候选区域的大小，但子图匹配的过程是基于VF2算法，时间复杂度随查询图增大呈指数上升。

(a) AIDS

(c) YAGO2图5 不同算法的平均查询响应时间变化曲线

上述实验结果表明：VF-SMDS在结构稠密数据集表现最好，在结构稀疏数据集上的平均查询响应时间优于GADDI、SPath、VF2++和SubISO算法，对于规模较大结构复杂的查询图平均响应时间也优于GADDI、SPath、SubISO、VF2++和VF3。在数据集构建时间上，VF-SMDS在六种算法中表现仅次于VF2++和VF3，数据集的存储空间明显优于GADDI、SPath和SubISO。因此，从三组实验中共同得出结论，针对大规模数据图子图匹配，VF-SMDS效率更高。

4 结 语

为了提高子图匹配的效率，提出了一种基于图连通支配集的子图匹配优化算法——VF-SMDS。首先，通过贪心算法获取查询图的最小连通支配子图；然后，利用代价模型确定最优k查询节点匹配序列；最后，利用支配节点的结构信息对搜索空间进行有效剪枝。本文分别采用了AIDS Antiviral数据集、Yeast数据集、YAGO2数据集并与主流算法(GADDI,Spath)和近几年的算法(VF2++、SubISO、VF3)进行实验对比，验证了VF-SMDS的可扩展性和高效性。实验结果表明：在处理大数据图、查询图规模较大、查询图节点较多的情况下，VF-SMDS的查询时间更少，效率更高。未来工作将对VF-SMDS进行充分研究，将VF-SMDS应用在分布式处理平台上，进一步研究支配节点对子图匹配的影响。