“瓜豆原理”在解题中的应用——以一个线段最值问题为例

傅旭丹

(杭州外国语学校，浙江 杭州 310023)

章建跃博士认为：数学教学的主要目标就是使学生在获得“四基”和“四能”的过程中发展思维能力[1].这与变式教学中“通过不断迁移问题的非本质属性、不断变更思维角度来把握问题本质、提高思维能力”的教学模式不谋而合.初中阶段经常会碰到一类由于动点而产生的线段最值问题，解决这类问题的关键在于明确动点的运动轨迹.特别是碰上多动点的情况，具体操作起来难度非常大.近期，笔者在初三培优班与学生一起探究了一个双动点问题，在发掘解决方案的同时做了一些推广，并引导学生探索变式，与同行分享.

1 原题呈现

图1

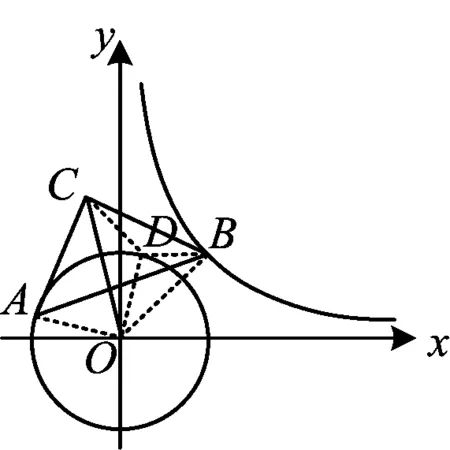
图2

参考答案的解答十分简洁漂亮，但事实上很难想到这样的解决方法.课后笔者继续探究，整理出4种解决方案.由于解决这类问题的关键在于明确动点的运动轨迹，利用几何画板，先固定点B的位置，发现点C的轨迹是一个圆；然后利用直角和熟知的“一线三垂直”模型求解.

图3

当m=2时取到等号.

评注“一线三垂直”是初中阶段的典型模型，以上解法还用到了求点的轨迹的“相关点法”.明确点C的轨迹后，OC的最值就可以考虑了，但最后一个环节用到了基本不等式，这是初中学生不具备的能力，有一定的局限性.

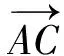
=(x-s,y-t),

因此

代入s2+t2=4得点C的轨迹方程为

当m=2时取到等号.

评注从解题过程可以看出，解法2比解法1更有一般意义，它跳出了直角这个条件的限制，进一步改变△ABC的形状同样可以解决问题.向量与复数是相通的，于是得到解法3.

解法3设点A,C对应的复数分别是zA,zC.因为AC由AB绕点A逆时针旋转45°而得，所以

可变形为

由|zA|=2,得

下同解法1.

评注解法2和解法3都运用了高中知识，可以满足教师自己课余提升专业素养的需求.笔者通过探究上述解法，发现从动点的轨迹来看，如果固定点B，C的轨迹与点A保持一致也是圆；让点B动起来以后会得到无数个半径相等的圆，但这些圆的圆心轨迹与点B的轨迹保持一致.于是笔者想到了动点问题中的“瓜豆原理”，并在课堂上将原理介绍给学生，这对学有余力的学生来说是一个有趣的结论.这也顺应了《高中数学新课程标准(2017年版)》(以下简称《新课标》)提到的不同的人在数学上得到不同的发展的基本理念[2].

2 瓜豆原理

“瓜豆原理”也叫“朋成原理”，即当线段的一端固定，另外一端在某一图形上运动的时候，这条线段上的某个定点，或者和这条线段有着固定位置关系的某个点，会相应地运动出和前面某一图形相似的图形[3].如图4，线段一个端点在某个图形上运动时，其中点的运动轨迹和这个图形位似，位似比为1∶2；如图5，三角形的一个顶点绕另一个顶点在某个图形上运动时，第3个顶点的轨迹和这个图形相似.这里选取其中一种特殊情形来证明“瓜豆原理”.

图4 图5

结论1如果一个图形绕着一个定点，通过旋转和位似变换，使得某一对对应点在一个圆上运动，那么其他对应点的运动轨迹也是一个圆.

如图6，△ABC绕点A做旋转位似，使得点B的对应点B1始终在⊙O上运动，在运动过程中，求证：点C的对应点C1的轨迹也是一个圆.

图6 图7 图8

证明如图7，在⊙O上另取一点B2，使得△ABC∽△AB1C1∽△AB2C2.由手拉手模型易证△AB1B2∽△CC1C2.设△CC1C2的外接圆为⊙O1，在⊙O1上取点M，构造△AMN使得△ABC∽△AMN，下证点N在⊙O1上即可.同上可得△BB1M∽△CC1N,从而

∠CNC1=∠BMB1=∠BB2B1=∠CC2C1，

于是点N在⊙O1上.

如图8，利用几何画板跟踪动点C，即为⊙O1，我们可以直观地看到△AOO1∽△ABC.

有了“瓜豆原理”，我们可以快速解决例1.

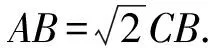
图9 图10

评注原题中有两个动点，我们两次运用“瓜豆原理”才可以解决.相比一个动点问题要困难一些，过程中需要理清定点、主动点、从动点之间的关系.解法2和解法3显然已经超出初中生的能力范围，想做进一步的探索就有必要了解并运用“瓜豆原理”.

3 引申推广

如果将原题中的等腰直角三角形改为更一般的三角形，在点A,B运动的过程中使△ABC保持相似，我们同样可以用向量法和复数法来解，但计算非常烦琐.笔者利用“瓜豆原理”将原题中三角形推广到一般情形，得到以下3个变式：

图11 图12 图13

分析固定点B，由于点A绕点B顺时针旋转θ角并伸缩至λ倍，A的轨迹是圆，因此点C的轨迹是一个以O1为圆心、λr为半径的圆，其中O1是由点O绕点B顺时针旋转θ角并伸缩至λ倍得到(如图12).

由O1B=λOB，∠O1BO=θ,可得

O1O2=O1B2+BO2-2O1B·BO·cosθ，

从而

当然，以上结果限定在点O位于⊙O1外的条件下.

评注将原题的等腰Rt△ABC推广到了任意三角形.如果换个角度，改变点A和点B的运动轨迹，师生可以利用“瓜豆原理”一起探索很多有趣的变式.

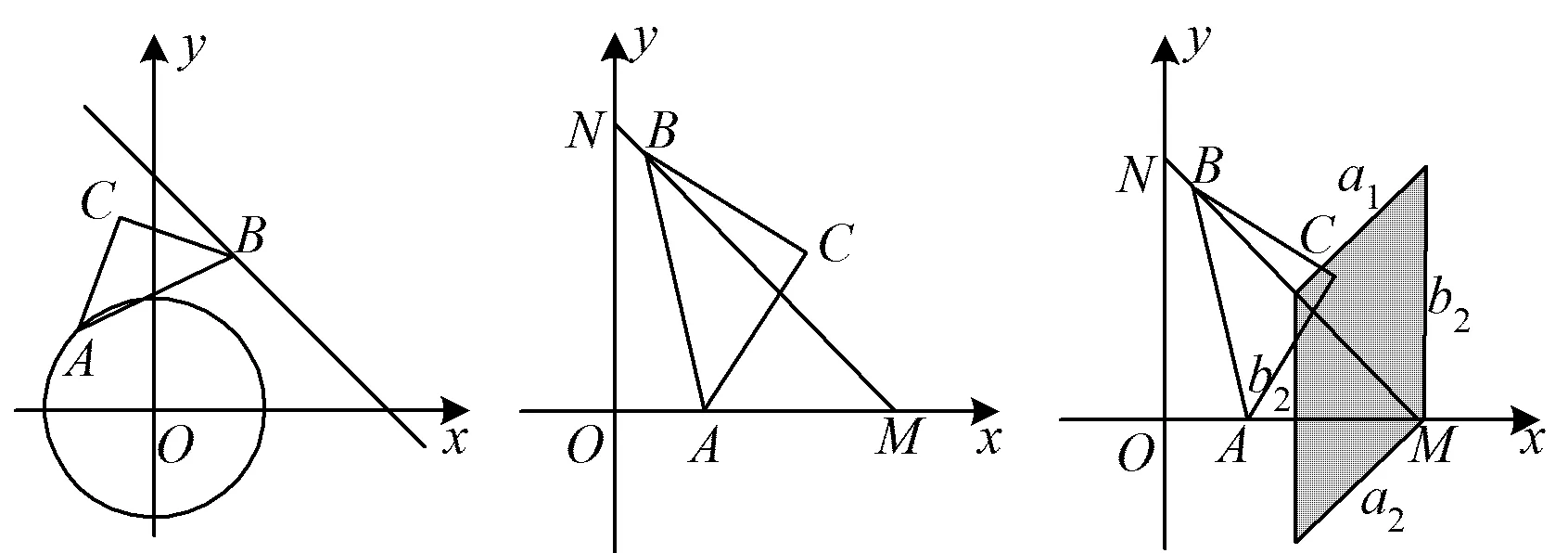
图14 图15 图16

变式3在平面直角坐标系中，△MON的顶点M(1,0),N(0,1)，A,B分别是边OM,MN上的动点.以AB为斜边作等腰Rt△ABC(如图15)，求点C运动轨迹形成区域的面积.

事实上，教师可以引导学生一起再更换动点A,B的函数图像类型，在运用“瓜豆原理”的过程中去熟悉并体会新工具的强大功能.

4 反思感悟

习题教学是一种常规的教学方式，学生的学与教师的教在题目的讲解传授过程中达成.在这个师生互动的过程中，题目的解决只是起点，而数学思维方法的归纳与提炼才是落脚点.“瓜豆原理”在解决旋转位似过程产生的动点轨迹问题中，可以避免烦琐的计算，直观形象，不失为适合初中学生的一款解题利器.通过原题将“瓜豆原理”介绍给学有余力的学生，让他们理解知识原理，之后碰到此类动点轨迹问题都可以借助这个强大的原理秒解难题.习题教学是对联系、转化、整合、综合、分析等数学方法的集中梳理，是引导学生经历真实性、高阶性思维活动的过程，这样的过程必将促使讲题教学既有宽度，也有高度，更有深度.《新课标》倡导要将培养“自主与创新”意识渗透到教学活动的各个环节，但这并不意味着教学活动是“信马由缰”,教师应该用“引导学生探究”来代替“牵着学生鼻子走”.在平时的教学过程中，我们经常会碰到一些有趣的题目，引导学生去改变其中的部分条件，往往会引申出一系列变式.此时解决原题的方法有可能行不通，那就需要寻找新的解题方法，不断解决变式的过程本身就是一线教师非常好的专业提升途径.在这个过程中，与学生一起归纳总结出适合变化前后的解题模型无疑是达成习题教学的高效路径.

数学学科核心素养本质上反映的是数学思维品质，基于核心素养的数学课堂应立足于学生的思维品质的培养而成为“思维之树常青”的课堂[2].把握问题的本质使“思维之树”苍翠挺拔，思维的动态迁移让“思维之树”枝繁叶茂，这种“不变”与“变”的辩证统一正是变式教学的魅力之所在.