挖掘教材重基础 培育思维提素养——对2021年德州市数学中考试题第24题的评析

杜 丽

(德州市第九中学，山东 德州 253000)

2021年山东省德州市数学中考第24题是一道有关圆的综合题，满分12分，考生平均得分只有2分，全市6.9万考生中仅27人得满分，是所有大题中得分率最低的题目.此题由易到难层层递进，重视对学生基础知识的考查，又关注了学生思维水平的达成，实现了从“知识立意”到“能力立意”的过渡，现结合试卷中反馈的信息做如下分析和研讨.

1 试题呈现

题目已知⊙O为△ACD的外接圆，AD=CD.

1)如图1，延长AD至点B，使BD=AD，联结CB.

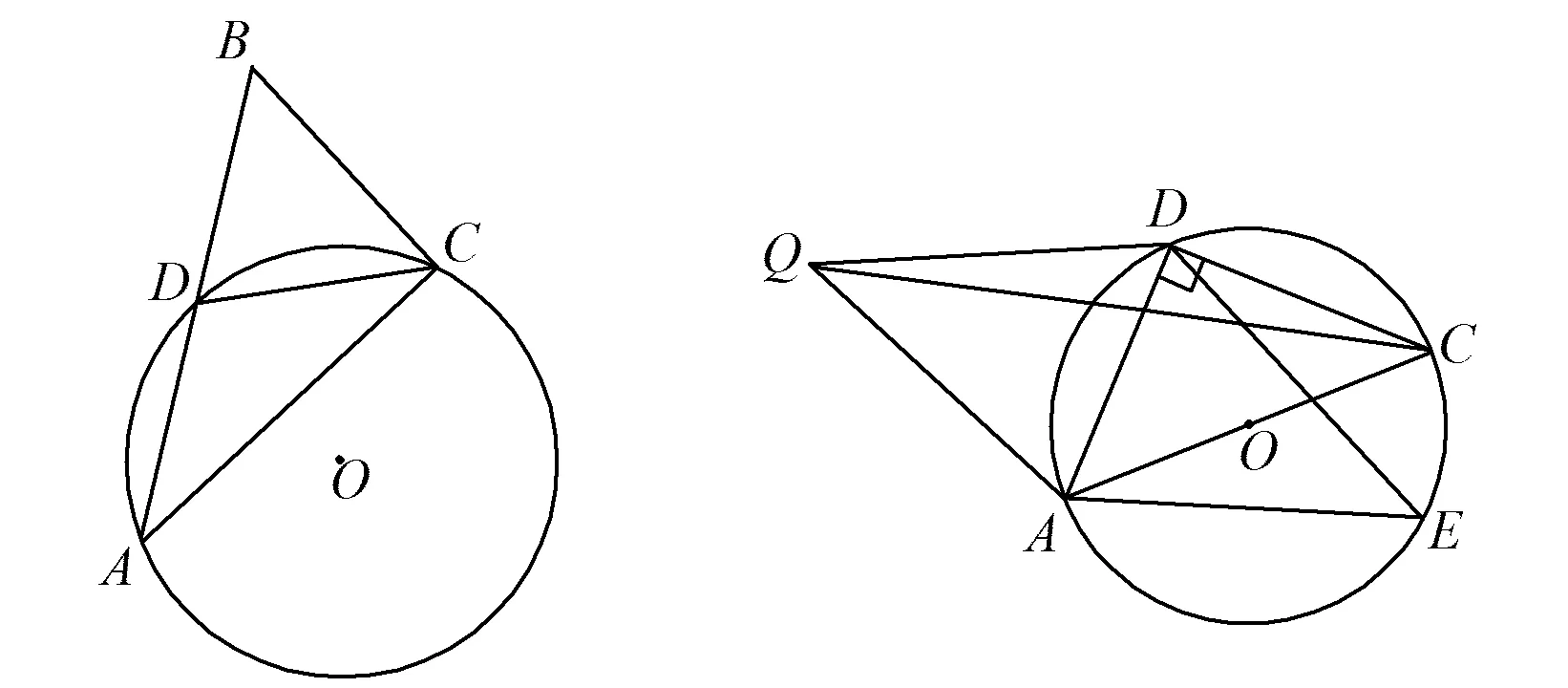
图1 图2

①求证：△ABC为直角三角形；

②若⊙O的半径为4，AD=5，求BC的值.

2)如图2，若∠ADC=90°，点E为⊙O上的一点，且点D,E位于AC的两侧，作△ADE关于AD对称的图形△ADQ，联结QC.请猜想QA，QC，QD三者之间的数量关系并给予证明.

考点剖析本题重点考查了圆的性质，如圆心角定理、圆周角定理、垂径定理等，还考查了等腰三角形的性质、勾股定理、轴对称的性质、全等三角形、相似三角形、旋转等知识，一题多解，一问多变，灵活性强.在问题的解决过程中，考查学生的几何直观、推理能力、对几何模型的抽象能力、运算能力、创新意识等核心素养.

2 一题多解

2.1 基础考查

第1)小题中的第①问源于教材，又高于教材，注重对核心基础知识的考查.对于“直角三角形斜边的中线等于斜边的一半”逆定理的证明，是对基本定理的深度思考，学生所用的方法多种多样，典型的思路如下：

思路1如图3，由等腰三角形的性质“等边对等角”，得到∠1=∠2，∠3=∠BCD，再由三角形的内角和为180°，可得

图3

∠1+∠2+∠BCD+∠3=180°，

即

∠2+∠BCD=90°，

得

∠ACB=90°.

这是此题最常规的思路.

思路2借助于方程思想，如图3，设∠1=x，用x表示△ABC的各个内角，∠2=x，∠BDC=2x，

∠2+∠BCD=x+90°-x=90°，

从而∠ACB=90°.

思路3如图4，由AD=BD=CD,可得点A,B,C在以D为圆心、AB为直径的圆上，由圆周角定理中“直径所对的圆周角是90°”，可得∠ACB=90°.

图4 图5

思路5由于定理“直角三角形斜边的中线等于斜边的一半”的证明源自课本中矩形的性质，有些学生回归到矩形.如图6，延长CD至点E，使DE=CD，由“对角线互相平分的四边形是平行四边形”，可判定四边形ACBE是平行四边形，再由”对角线相等的平行四边形是矩形”，可判定ACBE是矩形，从而∠ACB=90°.

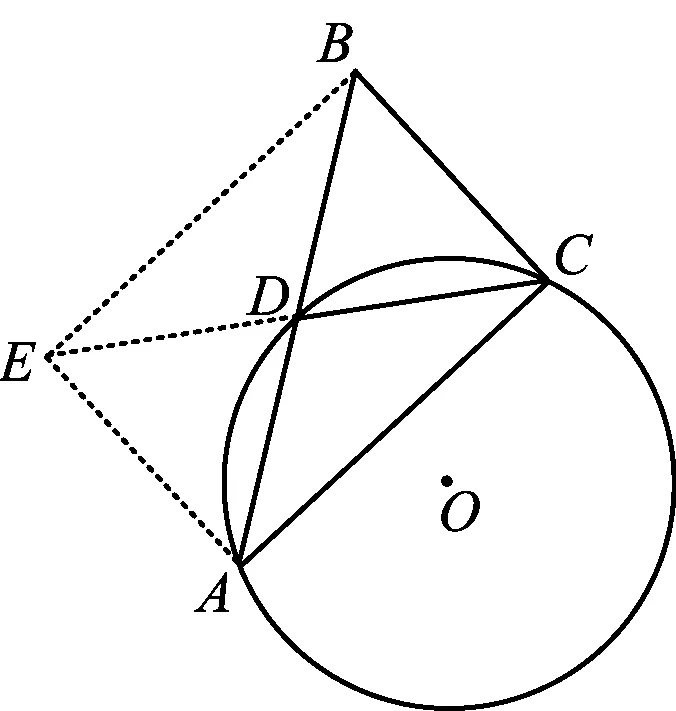
图6

2.2 深入探究

第1)小题的第②问是圆的性质与相似三角形的综合应用，是对学生的几何直观、推理能力、运算能力等核心素养的考查，素养立意，突出本质.由已知的半径和弦长为出发点，利用圆周角定理或垂径定理均可，分析方法较多，主要有以下5种思路：

思路1因为条件给出了半径的长，所以可借助“直径所对的圆周角是直角”构造出与Rt△ACB相似的直角三角形，再由相似三角形的性质求得BC的长.联结AO,DO,CO并延长都可出现直径，然后构造出直角三角形.多种作图方法均可，目的都是利用直径构造Rt△ACB的相似三角形.现给出其中一种证法(如图7).

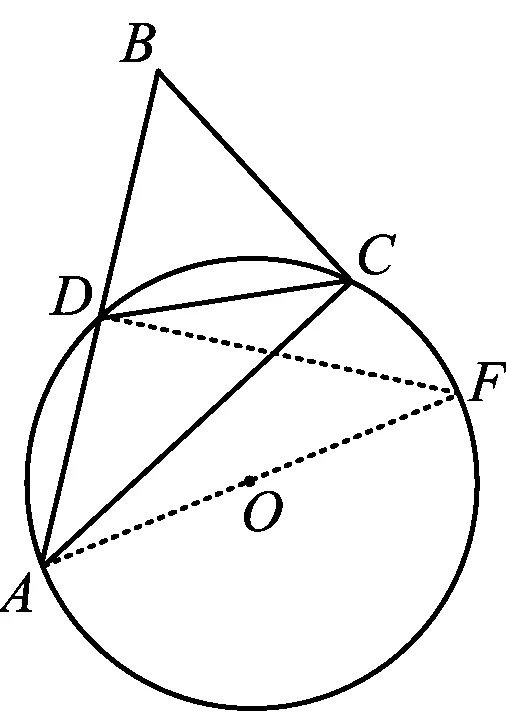
图7

解法1联结AO并延长，交⊙O于点F，联结DF.因为AF为直径，所以∠ADF=90°.又AD=CD，则

∠BAC=∠DCA.

由∠DCA=∠DFA,得

∠BAC=∠DFA,

又∠ADF=∠ACB=90°,从而

△ADF∽△BCA,

于是

因为⊙O的半径为4，AD=5，所以

AF=8，AB=10,

从而

故

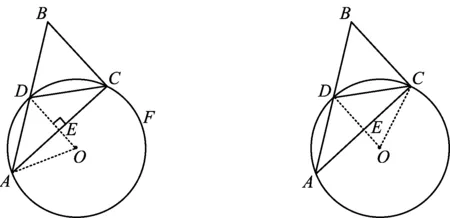
图8 图9

从而

(或根据三角形的中位线定理求得BC.)

思路4由已知半径想到联结OD,OC或OA，为了构造与△ABC相似的直角三角形，想到在弦AD或CD上作垂线，判定△ABC∽△OCM，再利用相似三角形对应边成比例求得BC(如图10).

图10

思路5如图10，在△ODC中，利用面积相等法，可得

DC·OM=OD·CE,

即

在△ABC中，利用勾股定理，可得

评注此方法易计算出错.

2.3 发散思维

第2)小题是对学生抽象能力、创新意识的考查，突出对学生思维能力的训练.本题主要看学生能否抽象出“手拉手”几何模型进行迁移应用，难度较大，大部分学生无从下手，找不到切入点，不会分析，能答对的学生寥寥无几，此题的典型思路有以下3种：

思路1要得到QA,QC,QD三者的关系，可猜想将三边转化到一个三角形中.由等腰Rt△ADC想到构建“手拉手”模型，以DQ为直角边作等腰Rt△QDP，证明△QDC≌△PDA;或利用旋转，将△QDC绕点D顺时针旋转90°，也可得到等腰△PDA.两种方法都可以把QC转化为PA，这一步是本问题的突破口.然后通过角的转化得到∠AQP=90°，通过勾股定理得到QA,QP,PA的关系，继而转化为QA,QC,QD的关系(如图11).

图11

解法1以DQ为直角边作等腰Rt△QDP，其中∠QDP=90°，联结AP.因为∠ADC=90°，所以

∠PDQ=∠ADC,

从而

∠ADQ+∠ADC=∠ADQ+∠PDQ,

即

∠QDC=∠PDA.

在△QDC和△PDA中，

从而

△QDC≌△PDA,

于是

QC=AP.

因为∠ADC=90°,AD=CD,所以

∠ACD=45°,

得

∠AED=∠ACD=45°.

由于△ADE关于AD的对称图形为△ADQ，因此

∠AQD=∠AED=45°,

又△PDQ为等腰直角三角形,从而

于是

∠AQP=∠AQD+∠DQP=90°,

得△APQ为直角三角形,进而

QA2+QP2=AP2,

即

故

QA2+2QD2=QC2.

思路2要得到QA,QC,QD三边的关系，以QC为斜边可以构造一个Rt△QNC(如图12)，可得

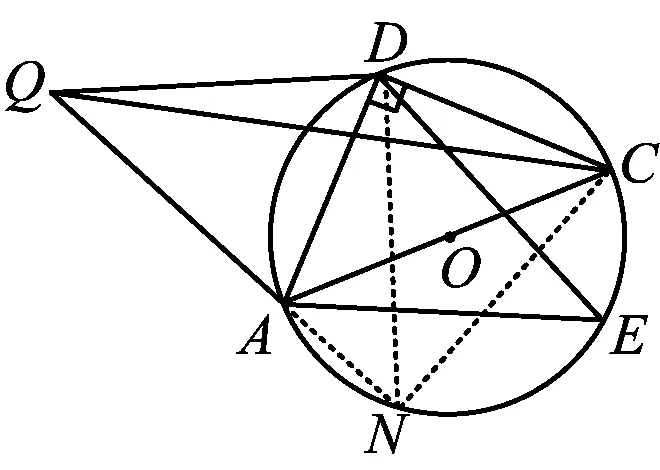
图12

QN2+NC2=QC2.

需将QN,NC转化为QD,QA，通过证明△QDN为等腰直角三角形，求得QN与QD的关系，再证明△QDA≌△NDC，可得NC与QA的关系，从而找到QA,QC,QD三边的关系.

解法2延长QA交⊙O于点N，联结CN，DN.由∠ADC=90°,AD=CD,得

∠ACD=45°,

从而

∠AND=∠AED=∠ACD=45°.

因为△ADE关于AD的对称图形为△ADQ，所以

∠AQD=∠AED=45°,

从而

∠AND=∠AQD=45°,

于是

QD=DN, ∠QDN=90°.

在等腰Rt△QDN中，

QN2=2QD2.

又因为∠QDN=∠ADC=90°,所以

∠QDN-∠ADN=∠ADC-∠ADN,

即

∠QDA=∠NDC.

在△QDA和△NDC中，由

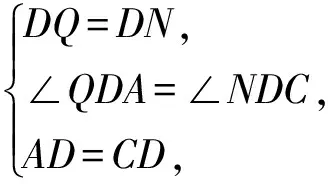
知

△QDA≌△NDC,

于是

QA=NC.

又因为AC为直径，所以

∠ANC=90°.

在Rt△QNC中，

QN2+NC2=QC2,

即

2QD2+QA2=QC2.

思路3以AD=CD，∠ADC=90°为突破口，在EC的延长线上截取CN=AE，达到将△ADE绕点D逆时针旋转90°的目的，从而逆时针构造出“手拉手”模型.通过模型，一是易证△NDE是等腰直角三角形，可知NE与DE的关系，从而由对称性转化为NE与QD的关系;二是证明△QDC≌△NDA，可得QC=NA.最后在Rt△AEN中，将NE,AE,NA三边的关系转化为QA,QC,QD的关系(如图13).

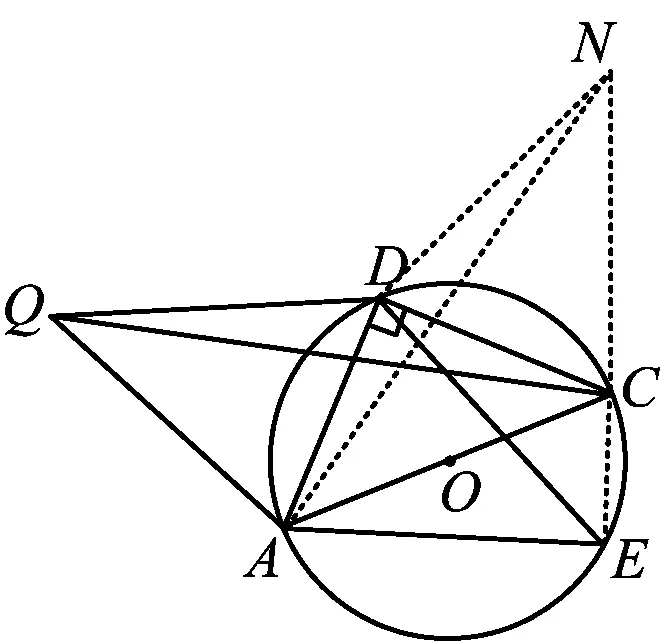
图13

解法3联结EC并延长，截取CN=AE，联结AN,DN.因为四边形AECD为圆内接四边形，所以

∠DCN=∠DAE.

在△DAE和△DCN中，由

知

△DAE≌△DCN,

于是

DE=DN, ∠ADE=∠CDN.

因为∠ADC=90°,AD=CD,所以

∠DAC=45°,

从而

∠DEC=∠DNC=∠DAC=45°,

于是

∠NDE=90°.

在等腰Rt△DNE中，

EN2=2DE2.

因为△ADE关于AD的对称图形为△ADQ，所以

DE=DQ,EA=QA, ∠ADE=∠ADQ,

从而

EN2=2DQ2,

于是

DQ=DN, ∠ADQ=∠CDN,

因此

∠ADQ+∠ADC=∠CDN+∠ADC,

即

∠QDC=∠NDA.

在△QDC和△NDA中，由

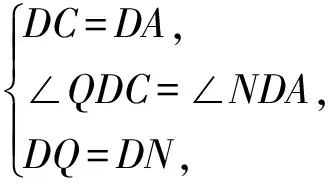
知

△QDC≌△NDA,

从而

QC=AN.

又因为AC为直径，所以

∠AEC=90°.

在Rt△AEN中,因为AE2+NE2=AN2,所以

QA2+2QD2=QC2.

3 错误分析

3.1 基础不扎实，定理不牢固

本题的3个问题难度分别是易、中、难，每一问各占4分，前两问得分率也很低.对于第①问，有近一半的学生将定理“直角三角形斜边上的中线等于斜边的一半”逆用，由已知的三边相等直接判定出直角三角形，没有证明过程得0分.这个定理是在人教版《数学》八年级下册“平行四边形”一章中矩形的性质里出现的，由矩形的对角线相等且互相平分证明得到，但很多学生只会正着用，逆定理不会证明，想当然地进行直接应用.可见部分学生在平时的学习中，对教材不够重视，对基本定理死记硬背，缺乏深度思考，导致知识记忆浅、理解差、易出错.

3.2 思维不清晰，方法复杂化

第1)小题的两个设问，方法较多，特别是第①问，由两次等边对等角即可证，但很多学生把简单的问题复杂化，对问题认识不透.对于第②问，很多学生不能有效审题，从条件中提取有用的信息进行分析，逻辑思维混乱.第2)小题则基本没有思路，数学知识、方法、思想等结构散乱，联系不够，迁移能力较弱.

3.3 过程不规范，计算不过关

第②问中的典型错误是由AD=CD两条弦相等直接用垂径定理得OD垂直平分AC，没有将弦相等转化为弧相等，都会扣分.这就体现了学生对定理的理解不透彻，几何证明过程不严谨.另外，还有部分学生思路正确，但最后计算出错，计算能力有待提高.

4 教学建议

4.1 立足教材，夯实基础

近几年的中考题大部分都来源于教材，有些是教材中的例题或习题的变式.教材是中考命题的最大资源库，更是数学知识与数学思想方法的重要载体.除了本题第①问中考查的直角三角形的基本定理，还有等腰三角形的性质“三线合一”，很多学生不经证明，直接逆用来判定等腰三角形，可见学生对教材中基本定理的理解停留在浅表层状态.因此，教师在教学中应深入挖掘教材，夯实基础知识，“题”尽其材，“例”尽其用，让学生多经历自主、合作探究的过程，体验知识的生成，而非死记硬背结论和定理.只有让学生经历了知识的探究过程，才能加深对知识本质的理解，增强对问题的洞察力.

4.2 培育思维，提升素养

学生答题过程中逻辑思维混乱的问题尤为显著，而数学的本质就在于数学思维.数学思维是指在思考和解决问题的过程中对数学思想、方法的合理运用能力.数学思维不是一种知识，而是一种能力[1].因此，在教学中，以基础知识为载体，应适时渗透类比、转化、数形结合等数学思想方法，揭示数学本质，逐步培养和提升学生的思维水平.

比如数形结合思想，从“函数图像信息提取”到“利用函数图像解决方程和不等式问题”，再到“利用函数解决线段、面积的最值问题”，始终贯穿于初高中数学.再比如转化思想、常用的边的转化和角的转化，这些方法在几何题目中处处都有应用.数学思想是对数学内容更为抽象和概括的本质认识，数学知识可能会被遗忘，但数学思想将伴随一生.在教学中，教师可从题目中提炼思想和方法，这有助于学生的思维走向深刻，也有利于数学核心素养的提升[2].

4.3 变式拓展，深度教学

第2)小题超低的答题率暴露了学生对几何基本模型的抽象能力和创新能力不足.教师在教学中要注重基本模型的提炼，如本题中的“手拉手”模型以及常见的“一线三等角”模型、课本习题中“一线三垂直”模型、半角模型等，充分运用基本图形，进行一题多变，一题多解，启发学生深度思考，有效拓展学生的思维.只有教师在遇到问题时“想多一点”“想深一点”“想开一点”“想透一点”“想异一点”，才能生成思维内涵丰富又灵动高效的课堂[3].