旨在有效迁移的解题反思

李昌官

(台州市教育教学研究院,浙江 台州 318000)

解题是手段，不是目的.当下学生数学解题不重视反思、不会反思、“买椟还珠，入宝山而空返”的现象普遍而严重，这极大地降低了数学解题教学的效益，加重了学生的学习负担.为了提高数学解题效益，除了指导学生学会审题，把解题教学的着力点放在数学思维上，把数学思维的着力点放在联想与预见上外，还需要加强解题后的回顾与反思，促进学生有效地积累解题活动经验，提高数学思维能力.

1 为什么应加强解题反思

首先，加强解题反思是由解题教学的目标与功能决定的.高考考过的题目通常不会再考，为什么还要做？很显然，是通过眼前的题目来学习某种方法、提升某种能力.一般来说，解题教学的目的有两个：一是解决眼前面临的问题；二是为了有效迁移而解题，即以眼前的问题为载体，以巩固知识、积累经验、发展思维、涵养品性为目的.就学生的学习与发展而言，第二个目的更加重要.没有反思的解题留下的只是一些零碎的、模糊的经验和一种情境化的直观感觉，它们难以成为日后有用的、能迁移到别的情境的经验，因此通过解题反思，使解题过程中无意识所获得的零碎、模糊的经验清晰化、条理化、逻辑化是一件十分必要的事情.

第二，加强解题反思是由认知和思维发展的基本规律决定的.皮亚杰把儿童的思维发展分为感知运动阶段、前运演阶段、具体运演阶段、形式运演阶段，并指出：感觉—运动性智力是思维的源泉，终其一生都以感知和实践性定势为中介，持续地作用于思维……感觉—运动性智力的活动只导致动作上的成功，而没有导致知识的真正掌握.因此，与具体情境紧密联系的解题过程、解题活动，即感觉—运动性智力活动是学生积累解题经验的基础，但难以形成清晰的可迁移的解题经验、解题策略促进心智的发展.只有当学生通过反思具体的、操作性的解题过程与解题活动，使自己对解题的认识达到“形式运演水平”时，才能真正形成解题经验，并使这些解题经验能够超越具体情境，迁移、运用到新的情境.认识论告诉我们，认识过程有两个基本阶段：感性认识与理性认识；感性认识需要通过去粗取精、去伪存真、透过现象把握本质来上升到理性认识.就解题教学的第二个目的——有效迁移而言，完成问题求解只是表明我们对问题解决的过程与方法有一个初步的、直观的感性认识，这个感性认识只有通过解题反思才能上升到理性认识水平.

第三，加强解题反思是数学解题大师们的共识.波利亚在《怎样解题》一书中将数学解题过程分为理解题目、拟订方案、执行方案、回顾等4个环节.数学教育家弗里德曼在《怎样学会解数学题》中将解题过程分为分析习题、做习题的图示、寻找解题方法、进行解题、检验解题、讨论习题、陈述习题答案、分析解题.解恩泽等在《数学思想方法》中提出：解题程序包括读题、审题、分析、拟定解题计划、实施解题计划、检验、解后研究等7个环节.罗增儒认为，学会解题需要经历4个阶段：简单模仿、变式练习、自发领悟和自觉分析.由上可看出：大师们普遍认为求得问题的结果并不意味着解题的结束，解题反思是一个必不可少的环节.尽管他们的用语(解题回顾、分析解题、解后研究、自觉分析)有所不同，但基本含义是清晰的、一致的.

第四，也是最根本的，加强解题反思是提高解题效益的需要.知识迁移本身并不难，但传统的教学过程没有让学生做好知识迁移的准备.其中一个问题是：知识的迁移要么是高端的反思性学习，从而实现有意识的、深思熟虑的迁移；要么需要低端的大量实地练习，从而实现无意识地、自动的迁移[1].解题是为了迁移，但迁移不仅不会自动发生，而且还有一个迁移的量与效率问题.学生在解题时不具备一般能力的基本原因是没有经常亲自动手进行分析，没有从中归纳出一般的运算方法及其理论依据[2].因此只有当学生由当前的问题解决形成具体化与抽象化、情境化与形式化相结合的清晰的经验，他们才能更好地发现当前问题与今后遇到的问题具有某种相似性、联系性，迁移才会真正发生.

2 解题反思，反思什么

解题是为了迁移，因此反思什么取决于我们期望迁移什么.《普通高中数学课程标准(2017年版)》指出：数学学科核心素养体现在情境与问题、知识与技能、思维与表达、交流与反思等4个方面.问题的情境是解题的条件与依据，问题的目标是思维的指南和方向.通过反思情境与问题，搞清楚情境的本质、问题的本质，有助于发现今后遇到的同类问题与当前问题的相似性，进而为有效迁移创造条件.知识与技能是解决问题的基础与依据.反思问题蕴含的知识与技能、及时弥补知识与技能的不足是有效迁移的基础.思维的缘由与依据、策略与方法是有效迁移的核心和关键.它们既是数学解题教学的着力点，也是解题反思的着力点.

例1如图1，AD与BC是四面体ABCD中互相垂直的两条棱，BC=2.若AD=4，且AB+BD=AC+CD=6，求四面体ABCD体积的最大值.

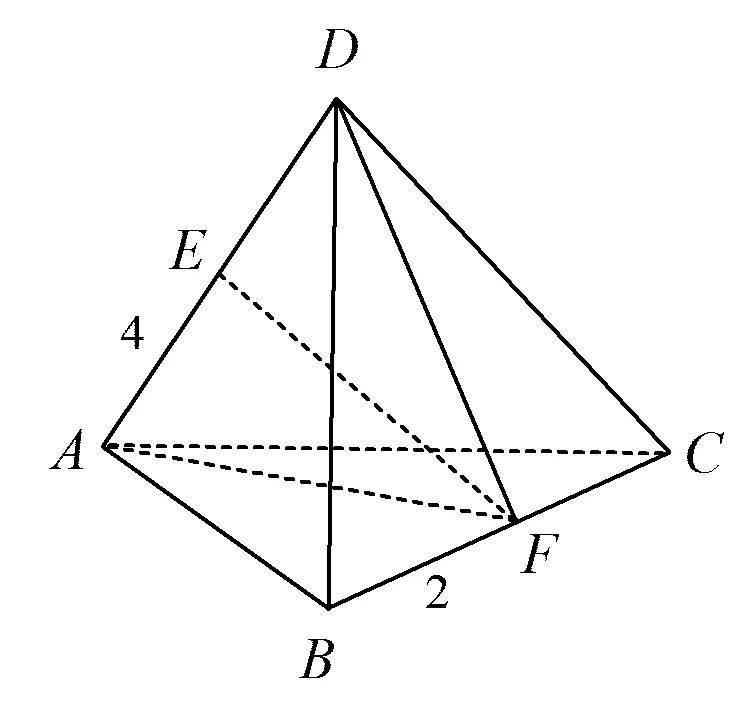
图1

解如图1，设EF是异面直线AD与BC的公垂线段.由AD⊥BC知BC⊥面ADF，因此

由AD=4，AB+BD=AC+CD=6，知点B，C在以点A，D为焦点、长轴长为6的椭球面上(如图2).由AD⊥BC知点B，C在与长轴AD垂直的截面的圆周上.

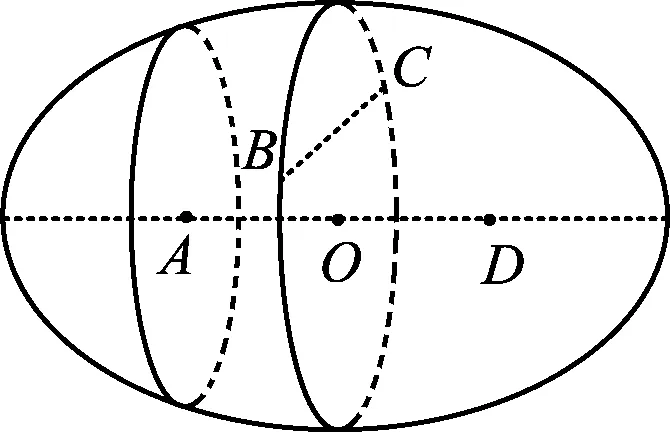
图2

反思1)情境与问题.这是一个以几何体及其体积为背景的函数最值问题.几何体及其所满足的条件是问题的情境，问题的目标指向是求这个几何体体积的最大值.情境“AD与BC是四面体ABCD中互相垂直的两条棱”蕴涵着求四面体ABCD体积的思路与方法.情境“AD=4，AB+BD=AC+CD=6”意味着从本质上看，动点B，C是满足一定条件的点的运动轨迹(如图2).由于此几何体的体积是由另一个相关量决定的、并随着它的变化而变化，因此这个问题本质上是一个函数问题.

2)知识与技能.此问题用到锥体的体积公式，为了简洁地求出体积还要对锥体进行分割；涉及椭圆的概念以及如何由椭圆概念生成椭球概念；还涉及线线垂直与线面垂直的相互转化，包括如果两条直线互相垂直，那么一条直线必在垂直于另一条直线的一个平面内(如图2)，以及如何求圆心到弦的距离等.

3)策略与方法.

策略与方法1分割求和.求四面体ABCD的体积，如果以△ABC为底面，那么不仅底面积难求，而且相应的高也难求.这就有一个如何分割、转化的问题.考虑到AD,BC的长度是已知的，且AD⊥BC，BC⊥面ADF，故可把四面体ABCD的体积看作是2个小四面体B-AFD与C-AFD的体积之和.

策略与方法3动静结合.如何理解和把握条件“AD=4，且AB+BD=AC+CD=6”的数学意义，取决于用怎样的视角看.联想椭圆的定义，不妨把A，D看作定点，B，C看作动点，这种动静结合的思想与观点往往是准确把握题设和目标的关键.

策略与方法5直观想象.在问题解决的过程中，无论是对四面体进行分割，还是发现点B，C的运动规律，或搞清楚EF何时取最大值，都离不开对图形的观察和观察基础上的想象.

例2如图3，一个四面体的3组对边长分别相等，且分别为1，2，t，当t变化时，求该四面体体积的最大值.

图3 图4

解根据题意，把此四面体看作长方体的一部分(如图4).设此长方体的长、宽、高分别为a，b，c，则

令t2=x,则3≤x≤5,且

令f(x)=-2x3+10x2+18x-90,则

f′(x)=-6x2+20x+18,

由f′(x)=0得

反思1)情境与问题.与例1类似，这是一个以立体几何为背景的函数最值问题.问题的情境主要是四面体的3对边长分别相等，情境的本质是具有某种特殊性质的几何体.该问题的目标指向是求该四面体体积的最大值，问题的本质是函数最值问题.

2)知识与技能.此问题涉及锥体体积公式、解三元方程组、恒等式变形、换元、利用导数求函数的最值等.

3)策略与方法.

策略与方法1正难则反.学生往往习惯于利用直接法和分割法求几何体的体积，在这两种方法都难以奏效的情况下，怎么办？用还原法、合并法.即把不规则或难以直接求体积的几何体通过扩张、还原、合并，得到规则的或比较容易求出体积的几何体.

策略与方法2联想与转化.即面对一个比较陌生的情境——四面体的3组对边长分别相等，能联想到什么，或能否追溯具有这种特征的几何体是怎样产生或得到的.在此问题中，联想到长方体相对的两个面的对角线相等，并把四面体体积问题转化为长方体体积问题是解题的关键.

策略与方法3扩张与还原.即在联想的基础上，把四面体扩张、还原成长方体.

策略与方法4函数思想.只有变化中的量才可能有最大值或最小值；而要求出这个最大值或最小值，就需要搞清楚它是依赖于哪个量的变化而变化，需要求出相应的函数表达式.更进一步，对一些复杂的最值问题，还需要借助研究函数的工具(如导数)等来解决.

通过反思，应形成如下信念：不仅问题的结论蕴涵在问题之中，而且解决问题的思路与方法也蕴涵在问题之中.我们应向审题要解题的思路与方法，向反思要解题思路与方法产生的规律性.

3 解题反思，如何反思

3.1 从因果关系入手，梳理解题思路产生的缘由与依据

思维就是有意识地努力去发现我们所做的事和所造成的结果之间的特定的联结，使二者连接起来[3].假如你正在观棋，要弄懂一盘比赛，仅仅知道棋子的走动规则是不够的.那只能让你辨认每一步都符合这些规则，这种知识没有多少价值……要弄懂棋赛完全是另一回事；必须了解棋手为什么不走这个棋子而走那个棋子……觉察出这一系列相继的步子并使其成为一种有机的整体的内在依据，这一本领对于棋手本人更为重要，对发明家来说也是这样[4].就数学解题教学来说，应强化两个思维过程：一是解题思路与方法的寻找与发现过程，这个过程具有较强的探索性和偶然性；二是梳理、明晰前一个思维过程所用的策略与方法的过程，这个过程具有较强的反思性和对思维方法的探索性.应通过反思，搞清楚解题思路和方法产生的缘由与依据，使偶然想到或很难想到的东西变得能够自然想到或容易想到.

3.2 从思维难点入手，明晰解题思路方法的核心与关键

问题解决是一个由许多思维片断组成的连续的过程，在这个过程中难免遇到这样那样的障碍.应在全面反思的基础上，搞清楚解题过程中“什么是决定性的一步，什么是主要困难，什么地方还可以改进，需要哪些知识和什么样的思路才能看到呢，有什么招数值得学一学，有什么东西在以后类似情况下仍能用到”[5].如例2中决定性的一步是如何把3组对边长分别相等的四面体扩张、还原成长方体；主要的困难是没有想到扩张、还原和不会扩张、还原；造成困难的原因可能是对长方体的几何特征缺乏深度的认识，以致无法建立所给四面体与长方体之间的联系.当然，思维难点往往因人而异.如例1，有的学生可能想不到把所给的四面体分割成2个容易求出体积的小四面体；有的学生可能难以发现点B，C在一个椭球面上运动；有的学生可能没有注意到线段BC必然在与直线AD垂直的截面上.

3.3 借助追问、抽象与感悟，明晰情境的本质、问题的本质、方法的本质

迁移并不是必然发生的，共同因素是迁移的基础；把技能和理解从一种经验带到另一种经验中去，所依靠的是两种经验存在着同样的因素[6].如果说审题的核心是搞清楚条件与结论的数学意义及其相互之间的联系，那么反思的核心就是要搞清楚情境的本质、问题的本质、解决问题思路与方法的本质.因为只有搞清楚情境的本质、问题的本质、方法的本质，才能更好地发现不同问题之间的相似性，进而做到有效迁移.搞清楚情境的本质、问题的本质、方法的本质是实现“解一题、通一类”“多解归一”的核心与关键.当然，在此基础上，还应注意不同问题之间的差异.如例1与例2，尽管二者都是求四面体的体积，但例1是用分解与分割的方法，例2是用扩张与还原的方法；二者都是求体积的最大值，但例1的最值是利用观察法直接得到的，例2的最值是借助导数才求得的.

3.4 反思的主体是学生，教师的职责是指导学生反思

正如解题与审题中经常出现教师越俎代庖现象，解题反思也经常这样.我们应切记：解题经验是靠每个人自身的实践与感悟获得的；解题反思的主体是学生，而不是教师；教师是学生解题反思的组织者、指导者.当然，学生学会解题反思并不是一件容易的事情，它离不开教师的示范，离不开教师对解题反思的框架性指导.在这个过程中，教师宜多采用元认知提示语并加强学生的解题反思实践.因为解题反思既是一种高层次的思维，也是一种技能、一种心智活动习惯与方式，它的养成离不开长期的解题反思实践.

4 结束语

应当学会这样一种对待习题的态度，即：把习题看作是精密研究的对象，而把解答习题看作是设计和发明的目标[4].应通过解题反思，形成清晰、简约、合乎逻辑、可迁移的问题解决的策略与方法，并使这些内化为自己的思维方式与思维习惯.