拆分数游戏 养分式运算 育裂项概念——分数、分式拆分与运算教学的创新设计

余继光

(柯桥中学,浙江 绍兴 312030)

分式概念及分式运算是数学的核心知识点之一.在分式单元复习时，将初中分式内容中的核心知识点进行创新设计已成为数学教育研究者的探究热点.分式拆分建立在分数拆分的基础上，创设分数拆分游戏，提升学生在抽象思维前提下的兴趣感，以较大跨度的知识范围将相互联系的分数、分式、分拆、扩分、裂项概念融为一体，为后续高中数学中复杂分式的运算奠定坚实的基础.

1 内容和内容解析

初中分数及分式运算是一个重要概念与基本运算，它涉及数学概念、运算规则、运算技术等，人教版《数学》八年级下册第16章安排了分式，并在此章中介绍了整数指数幂(含负指数幂).现将分式四则运算中一个重要的知识点(分式拆分)与小学的分数拆分及高中的分式裂项融合，进行教学上的创新设计，这样有助于完整的构建数学知识结构，为高中阶段大量复杂分式的运算打下良好的基础[1].

1.1 小学分数拆分游戏的创建

1)分数拆分为单位分数的概念；

2)通过拆分游戏将一个分数拆分成2个及以上单位分数之和.

1.2 初中分数(式)拆分的基本规则

1)分数拆分的基本原理；

2)将找约数、扩分与拆分联系起来；

3)分数拆分的基本步骤.

1.3 简单的分式裂项技术启蒙

1)分数(式)的裂项技术；

2)分数(式)裂项的简单类型；

3)分数(式)求和运算中的智慧.

2 目标和目标解析

将教学目标落实分成3个阶段：

1)分数拆分游戏阶段.通过游戏理解分数拆分的概念，并掌握分数拆分的技术，由4个游戏达成第一阶段目标.

2)分数拆分原理认识阶段.通过原理解读理解分数拆分概念，并掌握分数拆分的智慧，由下文中问题1的提出与解决达到理解分数拆分的原理.

3)分数拆分应用阶段.通过技术应用理解分式裂项概念，并掌握简单分式裂项的基本方法，由分数拆分自然过渡到分数(式)裂项，提供学生数学思维拓展的方法.

3 教学问题诊断分析

对于不同层次的初中生，教学过程中必会遇到一些问题，要随机应变，妥善处理：

1)对于分数分拆概念的形成，需要经过分数拆分游戏过程，学生在游戏前段可能会遇到小障碍，逆向思考是数学思维中的一种形式，也是学生数学学习的痛点，4个游戏实践体验后必能解除；

2)分数拆分方向比较抽象，是学生思维的一个障碍点，只能通过不断构建问题链、变式训练来理解并学会[2]；

3)分式运算方法与途径单一化是学生解决有关分式问题的痛点，在教学分数裂项过程中这也是一个难点，因为学生仍处在无序思维阶段，需要通过变式训练来完成.

4 教学支持条件分析

1)学生在小学期间已经学习过分数概念，因此问题情境对学生而言是非常熟悉的，这给学生认知提供了一个熟悉的情境，贴近学生的认知发展区；

2)分数拆分可以是一个团队的互助活动，通过同桌合作来完成，培养学生的合作精神；

3)数字感受是学生接触数学以后打下的基础，数字运算规则是学生必须掌握的基础，分式运算规则与性质是分式拆分的基础.

5 教学过程设计

实际的操作方法是：将其中5片每片平均分为2块，正好10块，每人拿一块；把剩余4片每片平均分成3块，一共12小块，每人再拿一块；还剩2小块，每块再平均分成5块，这样每个人可以再拿一块，正好平均分完.这样每个人分得的面包不仅数量相同，而且连大小和块数也是一样的.在这个故事中，从数学角度来看，就是将一个分数拆分成3个分数之和.

5.1 分数的拆分游戏创建

分子为1的分数叫做单位分数，将一个分数拆为几个不同的单位分数之和是一个非常有意义的问题.

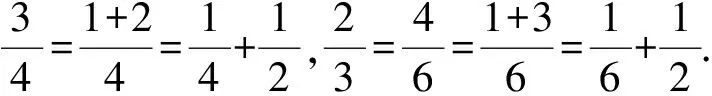
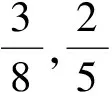
提出问题：以上将一个分数拆分成两个单位分数，能否将一个分数拆分成3个以上的单位分数呢？

……

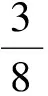
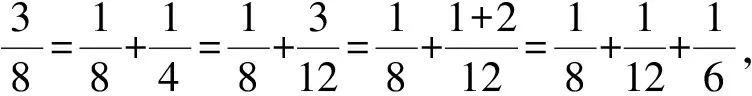
数字拆分游戏丰富了学生的数感，激起了学生的学习兴趣，其中的数学道理还需要教师进行讲解与点拨.

5.2 分数拆分原理讲解

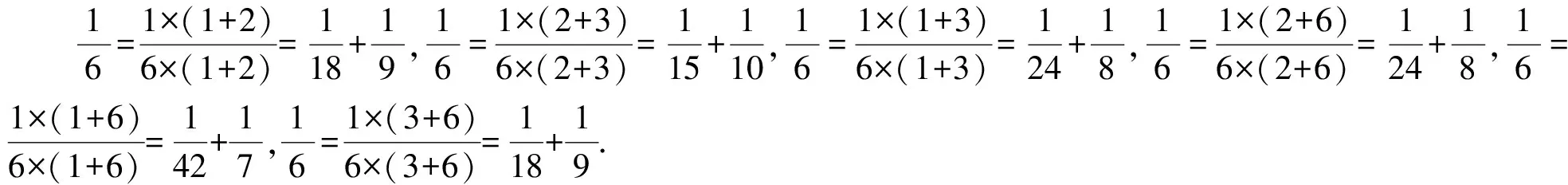
提出问题：以上结果相同的原因是什么？

原因：两个相加的约数，如果它们的比值相同，那么它们的结果也相同.

1)找出分母n的所有约数(找约数)；

2)将约数进行分组，比值相同的分为一组(分组)；

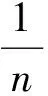
4)将所得分数拆成同分母的两个分数之和(或差)，使两个约数恰好是两个分数的分子(拆分)；

5)将各个分数分别约分，使分子为1，即变成单位分数(约分).

由此，学生了解了扩分的方法，寻找到分数拆分的基本方法及内在原理.

5.3 分数拆分与裂项

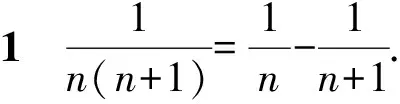
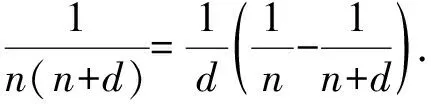
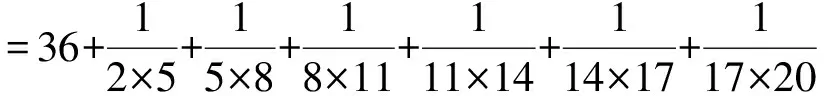
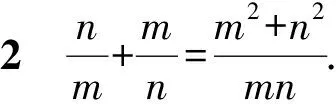
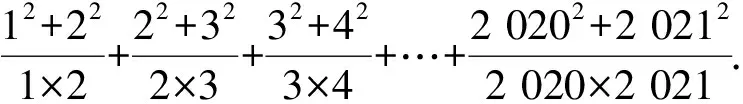
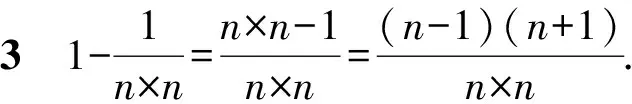
5.4 分式求和运算寻找最简途径

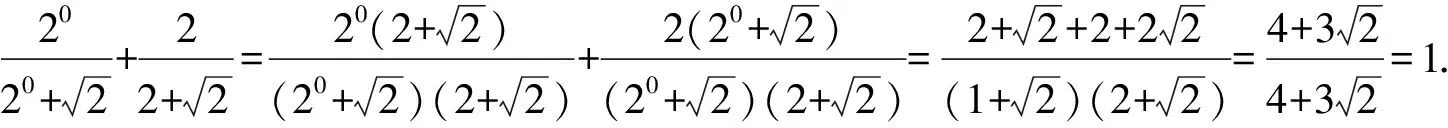
以上3种方法，最后一种最简单.

故M=6.

此题的计算方法很多，但是利用拆分的方法最简单，在分式运算中，拆分与裂项法有着异曲同工之效.

6 目标检测设计

评注裂项运算反映了学生的数字计算能力，观察规律用抽象代数式表达，如果只是一个数字计算题，那么首先要去找数字规律，即抽象表达能力要强，然后才是裂项运算能力.

分析设原式为M，首先考虑

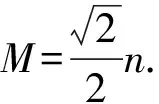
7 教学反思

7.1 人教版初中数学教材“分式”单元复习设计的优势与学习痛点

人教版《数学》八年级下册第16章(2008年6月第2版)安排“分式”内容，并在这一章介绍了整数指数幂(含负指数幂)，在单元复习教学设计时，融分式运算、分数拆分、裂项求和于一体，收到了较好的教学效果，这样安排的优势如下[3]：

1)整数指数幂(含负指数幂)内容安排在初中八年级，对于整个后续学习指数运算有极大的帮助，让学生在高一指数及指数函数学习前接触负指数幂，分解了高中指数内容的教学难点，即高中一年级学生学习指数内容时，已经能够熟练地进行整数指数幂运算，为分数指数幂奠定扎实的基础.

2)异分母分式相加减是学生学习的一个难点和痛点，大多数初中生到了高中还只有“通分”一个“死板”思路，很少有学生能抓住分母的特征，运用分式性质变异为同分母.由于已经接触负指数幂且了解了分式运算性质，问题6的设计弥补了这一缺陷，而且学生在初中阶段就可以顺利突破.

7.2 对学生概念理解存在差异的点拨

重视数学概念教学，在初中阶段，由于学生的数学思维开始分层(强、中、弱)，此创新设计对于数学思维能力中等以上的学生来说容易接受并理解.对于数学思维能力较弱的学生在教师的点拨下也能接受，特别是“分拆、扩分、裂项”概念以及复杂的分数(式)运算.