LINGO软件在高中数学建模中的应用研究
张峰,米永强
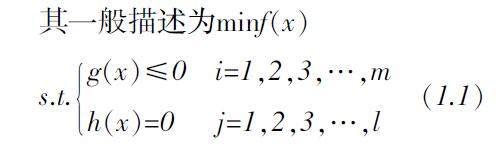
摘 要:文章在对高中数学的六大核心素养之一的数学建模和高中数学建模中的优化问题的研究基础上,针对高中数学建模竞赛中涉及的线性规划问题和0-1规划问题,给出了利用LINGO软件求解农场作物种植和大学生选课策略这两个案例的基本方法,数值实验结果表明,LINGO软件在求解该类问题中所花费的时间短且精确度高的优点,因此,高中数学建模爱好者可以将其应用于求解数学建模中的优化问题。
关键词:LINGO软件;数学建模;线性规划
一、国内外高中数学建模的进展
美国教师联合会在《中学数学课程和教学评估标准》中最早提出了高中数学建模。目前,国外高中数学建模竞赛主要有美国高中数学建模竞赛,该项竞赛是结合中学生所具有的特点进行设计的,竞赛队通常是由4名学生,外加一名指导教师组成,时间多数在每年11月第一周的星期五开始,由参赛队从当年所给出的两个实际问题中任选一个完成。荷兰从1990年开始至今,每年举办一次称之为A-lympiad的数学比赛来促进中学数学教育中应用数学的发展。为进一步普及数学建模教育,增强中学生的数学核心素养,美国数学及其应用联合会联合香港儒莲教科文机构于2014年创办了国际数学建模挑战赛,旨在鼓励各国的高中生积极主动地应用数学知识解决现实中的一些问题。
我国中学数学建模起源于1991年10月上海市举办的“金桥杯”中学生数学应用知识竞赛,在此影响和启发下,北京市从1993年开始举办同类型的中学生数学知识应用竞赛。为进一步改善我国基础数学教育的应用不足,普通高中数学课程标准《(实验)》(2003年版)提出,“高中数学课程应当提供一些基本内容的实际背景,以便更好地反映数学的应用价值,开展一些‘数学建模活动”。而随着我国的《普通高中数学课程标准(2017年版)》的颁布,已经非常明确地指出“数学建模”是高中数学的六大核心素养之一,并且将数学建模与数学探究活动作为主线之一。为更好地衔接高中数学与大学数学,提升高中生的团队合作方式解决现实问题的综合和创新能力,激发他们的应用数学的兴趣,并为国内外一流名校选拔数学专业有较大潜力的人才,清华大学联合中国工业与应用数学学会于2015年创办了“登峰杯”全国中学生数学建模竞赛,该项竞赛主要目的是考查参赛者如何将实际问题转化成数学模型、并借助于计算机通过编程求解数学模型的能力以及论文写作方面的能力。
二、优化问题与LINGO软件
人们在现实的生活、科学研究和生产等问题中经常需要从众多可行的方案中选择出最好的方案,比如,在生产计划中,如何做到既能提高产值,又能使获利最大;在资源的分配问题中,如何分配既能保证各方面的要求得到满足,又能使经济效益最大;在经济管理问题中如何做到使单位成本的产值最大或盈利最大等,一般把这类问题被称为最优化问题。
其一般描述为minf(x)
s.t.g(x)≤0 i=1,2,3,…,mh(x)=0 j=1,2,3,…,l (1.1)
其中f(x)∶Rn→R为目标函数,gi(x)∶Rn→R为约束函数。因为max{f(x)∶x∈S}=-max{-f(x)∶x∈S}且gi(x)≥0=-gi(x)≤0。故求解最大值问题都可以转换为最小值问题。
当问题(1.1)满足所有的变量是连续的、目标函数又是单目标且f(x)和gi(x)均是线性函数,则该问题就称之为线性规划问题,其求解通常是先写出满足题设的目标函数和约束条件;再根据约束条件进一步确定可行域;最后,求出目标函数在可行域内的最优解和最优值。但在实际问题中,当遇到的变量和约束条件都较多时,仅凭这样的求解方法则很难以得出最优解。当问题(1.1)中一部分变量取整数,另一部分取为实数就称之为混合整数规划问题;当变量都取为整数就叫整数规划问题;特别是变量只取整数 或 时,将此称为0-1规划问题。
0-1规划问题也是高中数学建模竞赛中经常会遇到的问题,因该问题对现实生活、生产有着重要的意义,它已被广泛地应用于航班安排、人力资源分配和背包问题等。其求解方法除了分支定界法、动态规划法和罚函数法等传统算法外,还有元胞蝙蝠算法、蜂群算法和粒子群优化算法等新型智能优化算法。但这些算法对高中生而言,相当抽象,所以就很难理解,而求解这类问题就可以用运筹学中一款简单、易于操作的数学软件-LINGO来实现。
LINGO软件是由美国的LINDO系统公司开发的一套专门用于求解规划问题和方程组问题的数学软件。该软件的优势不仅在于可以求解整数规划问题,而且程序编写简单、运行速度快。基于此,该软件已被越来越多的学者应用于求解交通运输,投资与决策,成本预算以及人力资源分配等各类优化问题。运用LINGO软件求解优化问题的方案通常是先结合所研究的实际问题,建立起数学模型,再对模型进行求解。
三、应用案例
案例1:农场作物种植问题
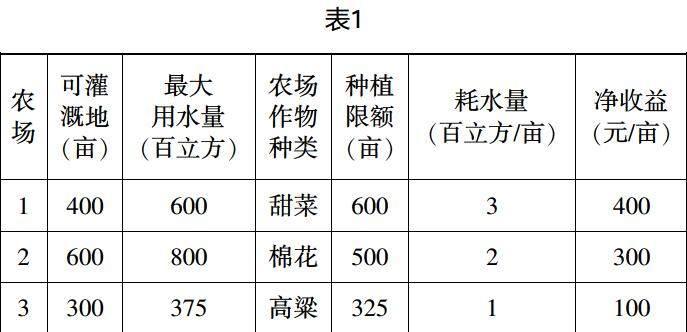
假设某一地区的一条灌渠可同时供就近的三个农场使用,各农场都可以种植甜菜、棉花和高粱三种作物,已知各农场的可灌溉地、分配到的最大用水量、各种作物的用水量、净收益及国家规定的该地区各种作物种植总面积最高限额如下表1所示:
三个农场达成协议,他们的播种面积与其可灌溉面积相等,在上述限制条件下,如何制定各农场种植计划使本地区的三个农场的总净收益最大。
分析:不妨用x1,y1,z1,x2,y2,z2,x3,y3,z3分别来表示农场1、农场2和农场3各自种植的甜菜、棉花和高粱的亩数,依据题意建立的模型如下:
Max=400(x1+x2+x3)+300(y1+y2+y3)+100(z1+z2+z3)
s.t.x1+x2+x3≤600y1+y2+y3≤500z1+z2+z3≤325x1+y1+z1≤400x2+y2+z2≤600x3+y3+z3≤3003x1+2y1+z1≤6003x2+2y2+z2≤8003x3+2y3+z3≤375x1,y1,z1,x2,y2,z2,x3,y3,z3≥0
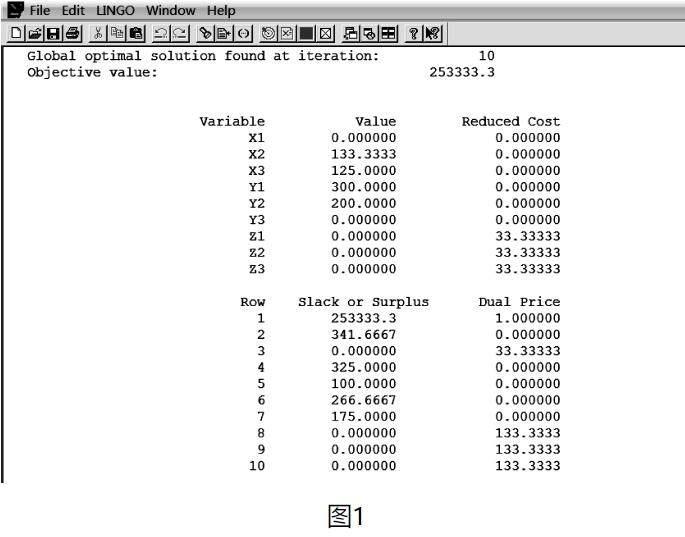
利用LINGO软件求解程序如下:
MODEL:
max=400*(x1+x2+x3)+300*(y1+y2+y3)+100*(z1+z2+z3);
x1+x2+x3<=600;
y1+y2+y3<=500;
z1+z2+z3<=325;
x1+y1+z1<=400;
x2+y2+z2<=600;
x3+y3+z3<=300;
3*x1+2*y1+z1<=600;
3*x2+2*y2+z2<=800;
3*x3+2*y3+z3<=375;
END
由此可知,最大总净收益为253333.3元。
案例2:选课策略问题
某大学数学与统计学院在运筹学专业的大学一年级新生中开设以下课程,如表2所示:
学院规定,大一年级的学生在学期末至少选两门计算机课、两门数学课和三门运筹学课,为了选修课程门数最少,应学习哪些课程?
该问题的数学模型:xi=1 选中课号为i的课0 未选中
Min=x1+x2+x3+x4+x5+x6+x7+x8+x9
利用LINGO软件求解程序如下:
min=x1+x2+x3+x4+x5+x6+x7+x8+x9;
x1+x2+x3+x4+x5>=2;
x3+x5+x6+x8+x9>=3;
x4+x6+x7+x9>=2;
2*x3-x1-x2<=0;
x4-x7<=0;
2*x5-x1-x2<=0;
x6-x7<=0;
x8-x5<=0;
2*x9-x1-x2<=0;
@bin(x1);@bin(x2);@bin(x3);@bin(x4);@bin(x5);@bin(x6);@bin(x7);@bin(x9);
END
因此,该专业学生至少选修6门课程,学习微积分、计算机模拟、计算机编程、数学实验课程、线性代数和应用统计。
该文研究了LINGO软件求解农作物种植计划和大学生选课这两个优化问题的基本方法,从程序运行时间和数值结果可看出,LINGO软件求解此类问题的速度和精确性较传统算法有显著的优势。因此,一线数学建模指导教师在数学建模培训中可以将LINGO软件作为培训的数学软件之一。
参考文献:
[1]中华人民共和国教育部. 普通高中数学课程标准(实验)[M]. 北京:北京师范大学出版社,2003.
[2]中华人民共和国教育部. 普通高中数学课程标准(2017年版)[M]. 北京:人民教育出版社,2017.
[3]唐加冕,周京徽. 线性规划问题在经济生活中的应用[J]. 商业时代,2011(19):10-11.
[4]陈宝林. 最优化理论与算法[M]. 北京:清华大学出版社,2005.
[5]朱光军,谭洁群,王云. 线性规划在数学建模竞赛中的应用[J]. 广西大学学报(自然科学版),2008,33(12):226-229.
[6]王熙照,贺毅朝. 求解背包问题的演化算法[J]. 软件学报,2017,1(01):1-16.
[7]李枝勇,马良,张惠珍. 0-1规划问题的元胞蝙蝠算法[J]. 计算机应用研究,2013,30(10):2903-2906.
[8]谢金星,薛毅. 优化建模与LINGO软件[M]. 北京:清华大学出版社,2006.
(责任编辑:莫唯然)

