n阶α次积分C半群扰动的指数有界性

刘乔乔,赵华新

(延安大学数学与计算机科学学院,陕西 延安 716000)

算子半群的扰动是算子半群的重要内容之一,近年来取得了显著的发展,且具有重要的应用价值,许多学者对此作了大量的研究工作。文献[1-3]中讨论了C半群以及积分C半群的扰动及相关问题;文献[4-5]中研究了双参数C半群的指数公式、谱以及扰动等;文献[6-8]中讨论了n次积分C半群的生成、扰动及其相关性质;文献[9-11]中给出了α次积分C半群的扰动定理;文献[12-13]中引入n阶α次积分C半群,给出n阶α次积分C半群的定义、基本性质及次生成元的性质,然后给出n阶α次积分C半群的预解式、预解方程等,解决了Cauchy问题。随后在文献[14-15]中研究了n阶α次积分C半群的生成定理、扰动、谱映射定理等相关问题。在此研究基础之上,还有一些n阶α次积分C半群的相关理论有待进一步研究。文献[15]中已经得到n阶α次积分C半群扰动的一个结果,本文对其得到的半群进行指数有界性估计,从而进一步完善n阶α次积分C半群的相关理论体系。

1 预备知识

X为无限维的复Banach空间,B(X)是X上有界线性算子全体所成的Banach代数;T(t)∈B(X),D(A)为线性算子A的定义域,设n∈N,α≥0,有

易知T(t)=0当且仅当存在n≥0,使JnT(t)=0,t≥0。

2 基本概念和引理

定义1设n∈N,α≥0,C∈B(X) 是单射,{T(t)}t≥0⊂B(X)强连续,若存在闭线性算子A使得[12]

(ⅰ) ∀x∈X,t≥0,JnT(t)∈D(A),

(ⅱ) ∀x∈D(A),t≥0,

当α=0时,{T(t)}t≥0是n阶C半群;

当C=I时,{T(t)}t≥0是n阶α次积分半群;

当α=0,C=I时,{T(t)}t≥0是n阶强连续半群。

定义2若Rc(λ,A)=λn-1(λn-A)-1C有定义在Banach空间X上的有界逆算子,则称λ为n阶α次积分C半群的次生成元A的正则点,Rc(λ,A)为A的C预解式,正则点的全体称为A的C预解集[13],记为ρc(A)。

引理1设A次生成n阶α次积分C半群{T(t)}t≥0,B⊂B(X),BA=AB,BC=CB,CB∈B(X)是单射,满足R(CB)⊂R(C)及A+B⊂CB-1(A+B)CB,则CB-1(A+B)CB生成n阶α次积分CB半群TB(t)可表示成为[15]

(1)

3 主要结果

引理2设A次生成n阶α次积分C半群{T(t)}t≥0,若‖T(t)‖≤Meωt,ω≥0,B⊂B(X),CB∈B(X)是单射,满足R(CB)⊂R(C),则对∀x∈X,t≥0有

M((ω+‖B‖)-ie(ω+‖B‖)t-

证明当i=1时,

‖C-1CB‖‖x‖·M(ω+‖B‖)-1·

(e(ω+‖B‖)t-1)=‖C-1CB‖‖x‖·

M[(ω+‖B‖)-1e(ω+‖B‖)t-

(ω+‖B‖)-1];

当i=2时,

(ω+‖B‖)-1]dt=‖C-1CB‖‖x‖·

M(ω+‖B‖)-1[(ω+‖B‖)-1e(ω+‖B‖)t-

t-(ω+‖B‖)-1]=‖C-1CB‖‖x‖·

M[(ω+‖B‖)-2e(ω+‖B‖)t-

(ω+‖B‖)-1t-(ω+‖B‖)-2]=

‖C-1CB‖‖x‖·

M[(ω+‖B‖)-2e(ω+‖B‖)t-

((ω+‖B‖)-2+(ω+‖B‖)-1t)]。

由归纳法可证:

证毕。

对引理1中得到的半群TB(t)有如下估计:

定理1设A次生成n阶α次积分C半群{T(t)}t≥0,若‖T(t)‖≤Meωt,ω≥0,B⊂B(X),BA=AB,BC=CB,CB∈B(X)是单射,满足R(CB)⊂R(C)及A+B⊂CB-1(A+B)CB,则CB-1(A+B)CB生成n阶α次积分CB半群TB(t)满足:

‖TB(t)x‖≤(α+1)!Me(ω+‖B‖)t· ‖C-1‖‖CB‖·

t≥0,x∈X,

‖TB(t)x-T(t)CBC-1x‖≤Meωt‖C-1‖‖CB‖·

证明对式(1)两边取范数可得

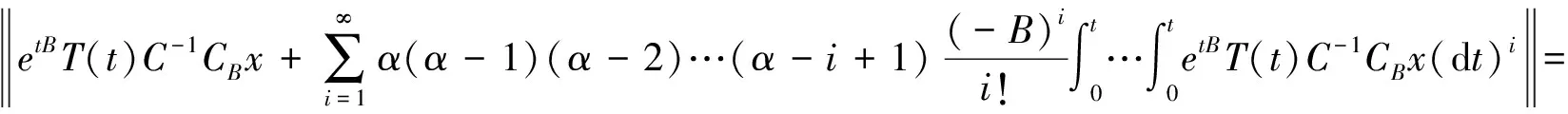
由式(1)得

两边取范数可得

‖TB(t)x-T(t)CBC-1x‖=

证毕。

4 结论

对n阶α次积分C半群的次生成元在有界线性算子的扰动下,得到的新半群进行指数有界性估计,且对新半群和原半群作差,得到2个重要结果。完善了n阶α次积分C半群的相关结果,丰富了算子半群理论的研究内容。