基于PCA-PLS的土壤重金属高光谱反演研究

崔 禹,韩 玲,韩霁昌,罗林涛,孙增慧

(1.长安大学地质工程与测绘学院,陕西 西安 710064; 2.长安大学土地工程学院,陕西 西安 710064)

土壤是一种难以再生的资源,是人类赖以生存的物质基础,保护土壤免受物理破坏,防治土壤环境化学污染,是推进生态文明建设和维护国家生态安全的重要内容[1-2]。传统的土壤重金属含量监测方法是基于常规的土壤采样后进行化学分析的方法[3-4],这种传统的监测方法较为昂贵且人力和时间消耗大,不利于区域性快速监测和评价。

近年来,随着高光谱技术的发展,光谱信息越来越丰富,高光谱技术被广泛应用于构建土壤重金属含量反演模型的研究中[5]。其中反演模型主要分为两类:统计分析模型[6]和机器学习模型[7],如郭云开等[8]将GMDH模型应用于Sentinel-2号遥感影像上,发现模型更加稳定可靠;吴希军等[9]采用NMF对原始能谱矩阵进行分段式分解,随后去除含水量引起的噪声,有效提高了模型的精度和鲁棒性;陶超等[10]比较了偏最小二乘回归和支持向量机分类,认为两种单一模型的迁移效果都无法满足定量模型的要求。

不管是统计分析模型还是机器学习模型,由于土壤光谱反射率是土壤中各种理化性质的一个累积效应,都需要结合光谱学与校准分离技术来预测不同土壤的重金属含量[11-13]。已有学者回顾了光谱方法在土壤重金属污染检测中的可能应用,强调了光谱方法的位点特异性强,模型普适性差[14]。这是因为土壤的不同理化性质存在非线性干扰[15],如刘彦平等[16]在综述中指出,目前高光谱遥感技术的理论基础还不完善,仅依靠实验数据的统计方法无法普适于不同环境条件下的定量反演,加强高光谱遥感技术的基础理论研究,有助于了解土壤重金属元素与高光谱遥感数据的直接或间接关系。

基于以上问题,本文选择陕西省的西咸新区和潼关县作为研究区域,提出了主成分分析(PCA,principal component analysis)与偏最小二乘的结合(PCA-PLS,principal component analysis-partial least square)模型,将该模型与单一偏最小二乘比较,并以斯皮尔曼相关系数和皮尔逊相关系数之间的关系为基准,探讨了不同预处理消除非线性干扰的效果差异,最后对PCA-PLS模型在GF-5号卫星影像上的应用进行了探讨。结果表明，PCA-PLS的反演效果优于单一偏最小二乘，2种相关系数的曲线具有一定的可视化非线性干扰的能力。

1 数据获取与预处理

1.1 仪器型号与参数

研究使用美国SEI公司生产的SR-2500便携式地物波谱仪,光谱范围350～2 500 nm;选用与仪器配套的软件DARWin SP V1.5对光谱曲线重采样,使生成的光谱反射率文件的波长间隔为1 nm。该软件可以选择仪器的积分时间为7.5～1 000 ms,较长的积分时间有助于消除部分噪声影响。

1.2 土样采集

在陕西省西咸新区([108.738°E,34.24°N]～[108.812°E,34.18°N])和潼关县([110.276°E,34.58°N]～[110.340°E,34.47°N])分别采集了500个和493个土壤样本。样本采集时,在约4 m2的范围内采集0～20 cm的表层土壤5份,总质量约2 kg,在自然条件下经风干、研磨并通过0.9 mm孔筛后,测量光谱反射率,并送检获得 Pb、Cu、Cd、Hg 4种重金属的含量。

1.3 光谱数据采集

在室内测量土壤光谱时,使用功率为100 W的卤素灯作为光源,光源照射方向保持固定。测量前,光谱仪探头在参考白板正上方10 cm处进行标准化;在放置参考白板的地方放置土样;用一次性硬纸片将土样上方刮平,将探头放在土样正上方10 cm处,测量土样的光谱数据。每测10个土样,需要重新参考白板,以避免周围光照情况变化导致的系统误差。

1.4 光谱数据预处理

研究在去除了350～399 nm和2 401～2 500 nm低信噪比的波段后,使用的光谱预处理方法包括标准正态变量变换(SNV,standard normal variate transformation)、一阶导数(FD,first derivative)、一阶差分(FDi,first difference)和对数变换lg(1/R)。上述预处理中,一阶导数和一阶差分在Originlab中完成,对数变换、SNV以及相关系数成图用Python语言编程实现。

2 模型与方法

2.1 偏最小二乘回归分析

传统的偏最小二乘回归(PLSR,partial least square regression)法是由 Wold等[17]提出的一种多因变量对多自变量的回归建模算法,该方法通过主成分分析提取的方式逐步构建新的综合变量,并剔除系统中的多重相关信息,有效地克服了变量间多重相关性在建模过程中产生的不良影响。本研究在每一种预处理结束后,使用PLSR进行建模与验证,PLSR的样本划分都用二十折交叉验证,即每次由95%的样本作为训练集,5%的样本作为验证集,最后得到的一次二十折交叉验证的结果为20次样本划分后结果的均值。

2.2 主成分分析与偏最小二乘的结合模型PCA-PLS

李民赞等[18]曾经提出了对土壤有机质含量和光谱数据都作主成分分析,随后建模回归的方法。本文在完全独立的情况下提出一个模型:先对土壤物质含量作PCA,得到的主成分矩阵作为因变量,与光谱数据进行PLSR,最后矩阵反解出各个物质含量的函数关系式,其表达式和推导过程如下:

(1)

(2)

(3)

YT=A-CBXT,

(4)

式(4)由式(1)～式(3)推得。式(1)～式(4)中物质含量Y可以是广义的土壤理化性质,包括但不限于各种有机物、无机物、土壤颗粒粒径、孔隙大小、pH值等,这个模型的精度理论上只受到Y变量维数不足的限制。

2.3 皮尔逊与斯皮尔曼相关系数

文献[11-16]中认为,土壤重金属的高光谱反演模型的好坏取决于消除干扰的多少。但一直以来,难以直观证明这是非线性干扰,也无法将这种干扰可视化。本文引入2种相关系数，并利用它们证明非线性干扰的存在以及可视化非线性干扰。皮尔逊相关系数要求2个变量都服从正态分布(可以正态化),而且2个变量中某一变量取任意值时,另一个变量标准差都相等,最后它描述的是线性相关性[19]。而斯皮尔曼相关系数既可以描述线性相关性,也可以描述非线性相关性[20]。2个相关系数曲线越接近,说明线性关系越强,即消除的非线性干扰越多；反之，2个相关系数曲线越疏远,说明存在的非线性干扰越多。

3 结果与分析

3.1 一阶差分与一阶导数

文献[1-2,5,8,10]中都采用过一阶导数或一阶微分作为一种预处理方法,但几乎没有学者讨论一阶导数和一阶差分2种预处理的异同点。二者的区别在于,前者是采用牛顿迭代法等数值分析方法拟合后的值,而后者是简单的Y值间隔差。图1由对某一样本的光谱反射率进行一阶导数和一阶差分得来，样本的原始光谱反射率单位为1，即取值范围0～1。图2由对自然指数exp(x)函数进行一阶导数和一阶差分得来。其他样本光谱反射率的一阶导数和一阶差分曲线与图1类似，也几乎完全重叠。本文推测这是因为二阶导数小,理由如图2所示,因为等距离散函数的一阶导数是拟合后的值,所以等距离散函可以看成是连续函数,即图2中虚线。选择exp(x)函数是因为它的二阶导数随着x的增加而增大。当x增大时,一阶导数(图2中切线)与一阶差分(图2中折线)的夹角变大,也就是它们的数值差距在变大,即不再相似。

图1 某样本光谱反射率的一阶导数和一阶差分曲线Fig.1 The first derivative and first difference curve of one sample's pectral reflectance

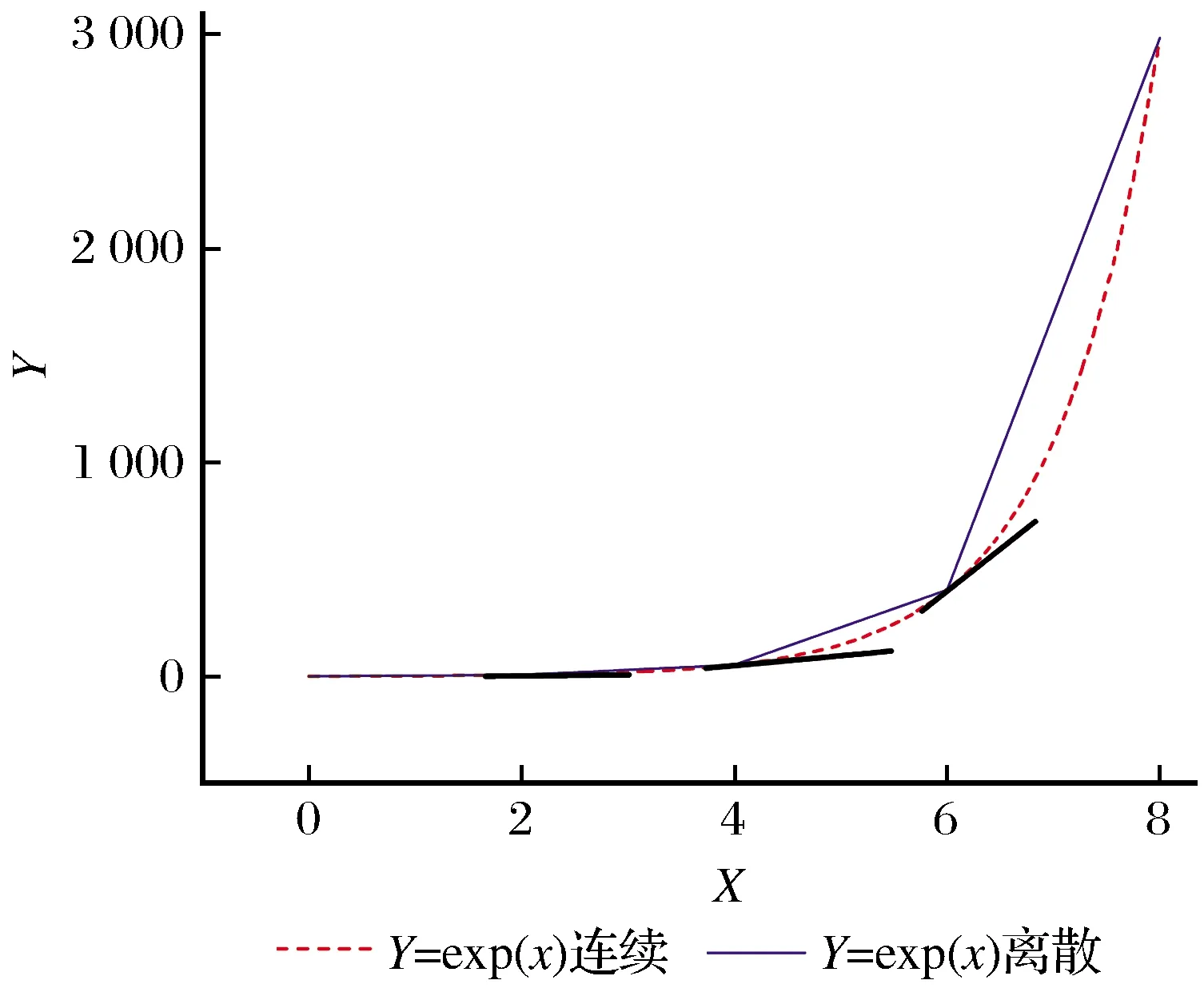
图2 exp(x)函数的一阶导数与一阶差分Fig.2 The first derivative and first difference of exp(x) function

为了验证推测一阶导数和一阶差分相似是因为二阶导数小,分析了2个地区样本光谱反射率的二阶导数,结果显示在潼关地区所有样本的所有波段的二阶导数绝对平均值为0.020 867 611,在西咸新区这一数值为0.008 337 614。arctan (0.020 867 611) ≈ 1.2°,潼关县样本的光谱反射率曲线倾斜度平均变化率为1.2°,西咸新区则更低。这也侧面说明,间隔1 nm的波段之间相关性很高,很难有突变值存在,突变值只存在于少数几个特征波段,这就是需要PCA和PLSR来消除多重相关性的原因。

3.2 2种相关系数曲线

4种元素所有样本的光谱反射率分别经过不同的预处理，各元素含量的2种相关系数曲线分别如图3～图6所示。由图3～图6可知,4个元素的原始光谱反射率与它们含量的2种相关系数曲线差距都较大,说明存在的非线性干扰较多,进行3种预处理后,2条曲线均有不同程度的贴近,这说明预处理确实消除了部分非线性干扰，与前人研究吻合[21]。并且SNV预处理后2条曲线更贴近，一阶导数FD不稳定且信噪比太低，这与表1中SNV后的R2更高、FD后R2较低相对应，这就将非线性干扰和模型精度联系了起来。

为了解释图3～图6中相关系数绝对值小的现象,特引出2个公式,分别为

(5)

(6)

式(5)表示皮尔逊相关系数满足t分布,式(6)表示斯皮尔曼相关系数满足正态分布。当样本数n很大时,即使很低的相关系数也能通过极显著性检验(p<0.01)。比如式(6),当样本数n达到401时,相关系数r达到0.116 5就代表极显著相关。

图3 4种预处理后Pb元素的相关系数比较Fig.3 Comparison of correlation coefficients of Pb after four kinds of pretreatment

图4 4种预处理Cu元素的相关系数比较Fig.4 Comparison of correlation coefficients of Cu after four kinds of pretreatment

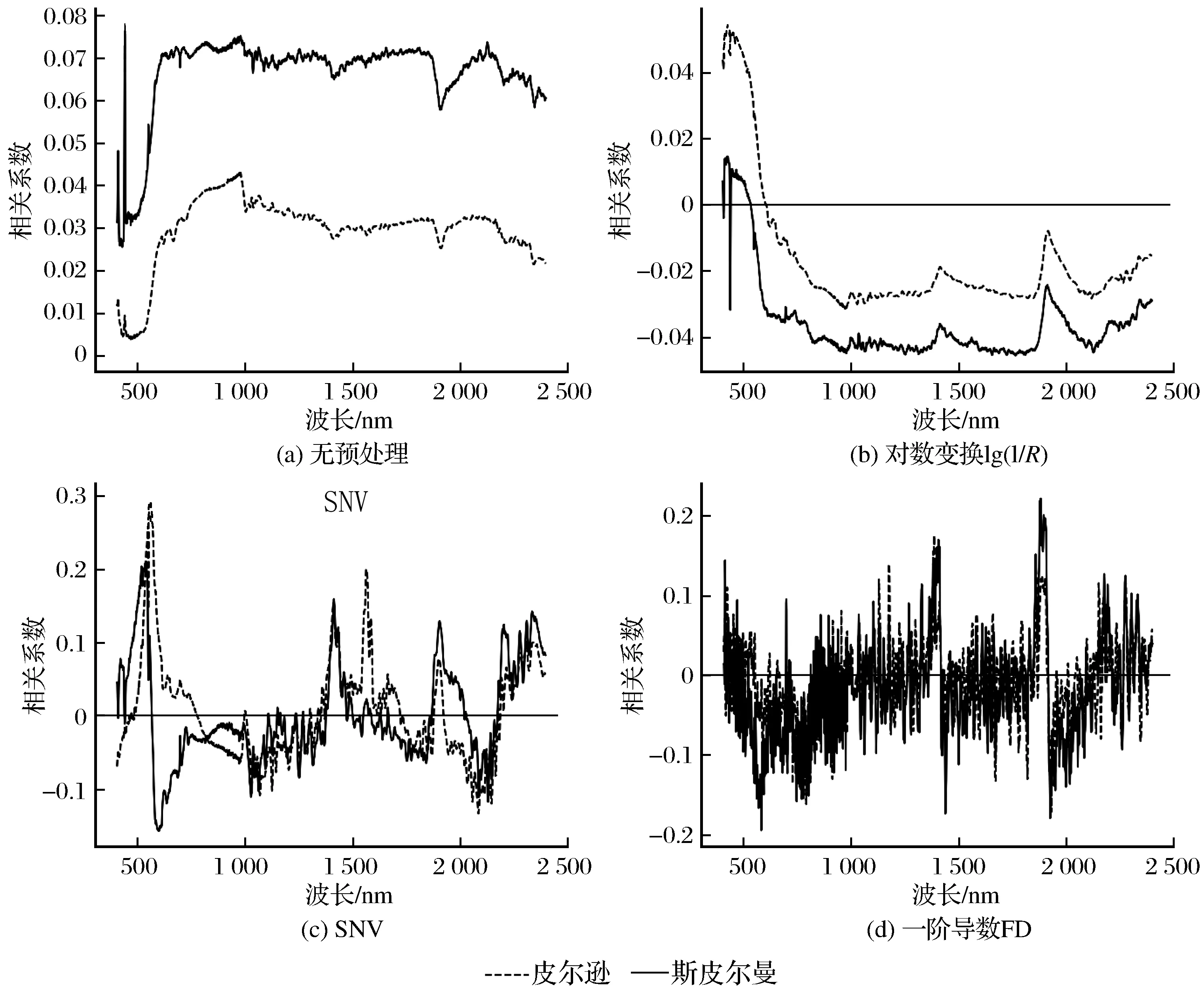
图5 4种预处理后Cd元素的相关系数比较Fig.5 Comparison of correlation coefficients of Cd after four kinds of pretreatment

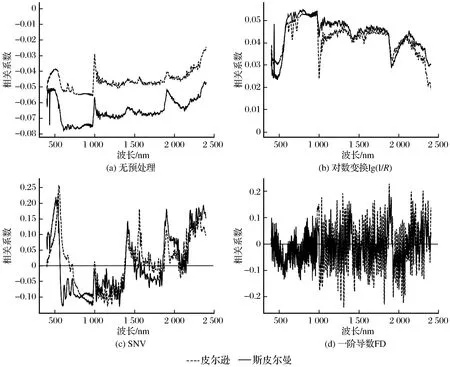
图6 4种预处理后Hg元素的相关系数比较Fig.6 Comparison of correlation coefficients of Hg after four kinds of pretreatment

3.3 普适性评价

本文选取了PLSR和PCA-PLS 2种反演模型,单一PLSR模型反演前还进行了3种预处理,在西咸新区建立这2种模型,并分别迁移到潼关县,比较了经过不同过程建立的模型的迁移效果。表1中比较了最佳预处理后PCA-PLS与不同预处理后PLSR的迁移效果,迁移成功率为2个区域的R2比值;PCA-PLS同样预处理的情况下,不仅在西咸新区建模的精度最高,模型迁移到潼关县的成功率也最高。其中Cd的迁移效果提升最大,比同种预处理后PLSR建模的成功率提高了20.9%,Cu提高了8.6%,Hg提高了7.2%,Pb的提升最小,提高了4.4%。以迁移成功率为标准,SNV预处理在3种预处理中效果最好,这一点也反映在图3～图6中,SNV预处理后2条相关系数曲线最接近,消除的非线性干扰也最多。

表1 4种重金属元素的迁移研究Table 1 Migration research of four heavy metals

3.4 PCA-PLS模型在GF-5号卫星上的应用

GF-5号卫星的光谱分辨率和空间分辨率都比较高,是目前最适合应用室内高光谱反演模型的高分卫星。本研究使用的两幅GF-5号卫星影像是在自然资源卫星遥感云服务平台申请的数据,在对其进行坏波段去除、坏线修复、条纹效应修复后进行波段融合。对融合后的影像进行辐射定标、大气校正、正射校正,最后用Python语言编程实现模型应用。潼关地区的4种重金属污染图如图7所示,其污染等级参考2019年土壤环境质量标准值。由图7可知,Pb与Cd元素的模型在卫星影像上的应用效果较好,污染情况与实地较为吻合,而Cu与Hg元素的模型应用效果很差,这可能是由于这2种元素在室内光谱和卫星光谱情况下的光谱特征差异大。西咸新区的4种重金属灰度图如图8所示。

4 结论

(1) 对于波长间隔为1 nm的高光谱数据,一阶导数和一阶差分2种预处理的效果相同。

(2) 迁移成功率可以部分反映消除非线性干扰的效果,对数变换Lg(1/R)、SNV、FD这3种预处理都能消除部分非线性干扰,SNV还能显著提高相关系数,消除干扰的效果也最好。

(3) PCA-PLS模型不仅建模的精度高,与同样没有预处理的PLSR模型相比,迁移成功率提高了20.9%,普适性更好。但本研究的Y变量维度较低,无法彰显PCA-PLS模型的优越性,今后将在Y变量维度多的研究中探讨此问题。

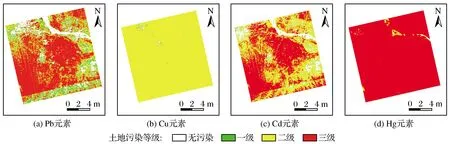
图7 潼关地区4种重金属的污染等级Fig.7 Pollution grade map of four heavy metals in Tongguan area

图8 西咸新区的4种重金属灰度图Fig.8 Gray scale map of four heavy metals in Xixian New Area

(4) 关于土壤重金属的卫星光谱反演模型,还有很大的研究空间。只有在卫星方面的研究成功了,才能完全体现出高光谱技术在探测土壤重金属含量方面的优势。