结合CEEMDAN的LSTM模型在滑坡变形预报中的应用

郭 睿,黄张裕,王尚祺,孙 瑞

(河海大学地球科学与工程学院,江苏 南京 211100)

滑坡监测是安全监测领域一项重要的研究内容,滑坡是具有极大破坏力的自然灾害之一,会造成建筑物、农田等损坏以及道路阻塞等,带来极大的财产损失甚至生命威胁。为了预防滑坡,减小财产及人员损失,需要对滑坡监测点的垂直位移进行持续监测,并对监测点的沉降变化做出预报,分析其现状和变化发展趋势。

滑坡是动态的变化过程,由于地质条件、荷载、地下水作用、边坡开挖、地震或打桩以及爆破震动等原因,会引起滑坡体发生滑移、沉降、倾斜、裂缝等变形情况[1-2]。沉降量监测无疑是一项非常重要的工作,其监测值是随着时间变化的随机序列,建立动态变化模型就能够对滑坡变形进行监测预报。

自回归滑动平均(ARMA,auto regressive moving average)模型及Kalman滤波等模型是时间序列预测中常用的方法,但神经网络的研究发展为时序数据的预测提供了新的研究方向。方毅等[3]将灰色神经网络应用在建筑物的变形预报中,发现其能够在小样本、贫信息和波动数据序列等情况下对变形监测数据做出比较准确的模拟和预报;刘思敏等[4]综合利用EMD和径向基神经网络,研究了大坝变形时间序列中非线性周期信号变化的内在规律,并通过对预测结果与实测变形差值的统计分析评价这一方法的预测水平;成枢等[5]将T-S模糊神经网络应用于变形预报中,发现其在长周期监测数据预报中具有优势;刘建[6]采用最小二乘与广义回归神经网络的组合模型法进行大坝变形预报,发现加入水位数据的组合模型预报精度有显著的提高。

LSTM模型在时序预测中的应用较为广泛,但在变形预报中的研究很少,且在具有明显自相关性的时间序列数据的预测中存在滞后性的现象。将CEEMDAN算法与LSTM模型结合,能够有效消除其滞后性,得到更高精度的预测结果。实验利用某滑坡监测点的沉降量数据,对比分析结合CEEMDAN的LSTM模型与单一LSTM模型、传统ARMA模型、Kalman滤波模型的预报精度,检验其有效性。

1 CEEMDAN算法

经验模态分解 (EMD,empirical mode decomposition) 算法是常用的信号分解方法,它采用三次样条法构建包络线,同时在分解过程中采取递归分解,因此会产生端点效应和模态混叠现象[7-9]。针对EMD算法存在的问题,集合经验模态分解 (EEMD,ensemble empirical mode decomposition) 算法在序列中加入高斯白噪声,避免了模态混叠,但仍有残余噪声在本征式分量(IMF)中传递。自适应完备集合经验模态分解(CEEMDAN,complete ensemble empirical mode decomposition with adaptive noise)算法由EMD算法、EEMD算法改进发展而来,它通过在分解时添加自适应白噪声并在得到IMF分量后立即进行加总平均计算,解决了前2种算法中存在的模态混叠和噪声问题,在有限次分解中能保证重构误差为0。

CEEMDAN算法的分解步骤可以分为3个阶段[10-12]。

(1) 在原信号中添加n组自适应白噪声,对其进行EMD分解得到的n个模态分量进行加总平均计算得到一阶模态分量,并与原始信号作差得到残余分量。一阶模态分量和残余分量的计算公式为

(1)

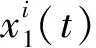
(2) 在上一次运算得到的残余分量中继续添加n组自适应白噪声,构成新的待分解信号,继续求解二阶模态分量及残余分量。二阶模态分量及残余分量的计算公式为

(2)

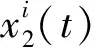
(3) 重复以上2个步骤直到信号无法继续分解,得到k个IMF分量以及最终的残余分量rk(t),原信号x(t)可以表示为

(3)

2 LSTM模型

长短时记忆(LSTM,long-short term memory)模型是递归神经网络(RNN,recurrent neural network)中的一种,它不仅继承了RNN能够记忆过去时间序列信息的优点,同时改进了其在反向传播中可能出现的梯度消失或梯度爆炸等缺点[13-14]。LSTM模型具有很强的时间序列拟合能力,能够解决神经网络中的长期依赖问题,其神经网络单元最主要的结构包括输入门、遗忘门以及输出门3个门控单元,分别控制数据的输入、筛选以及输出,其神经元结构如图1所示。

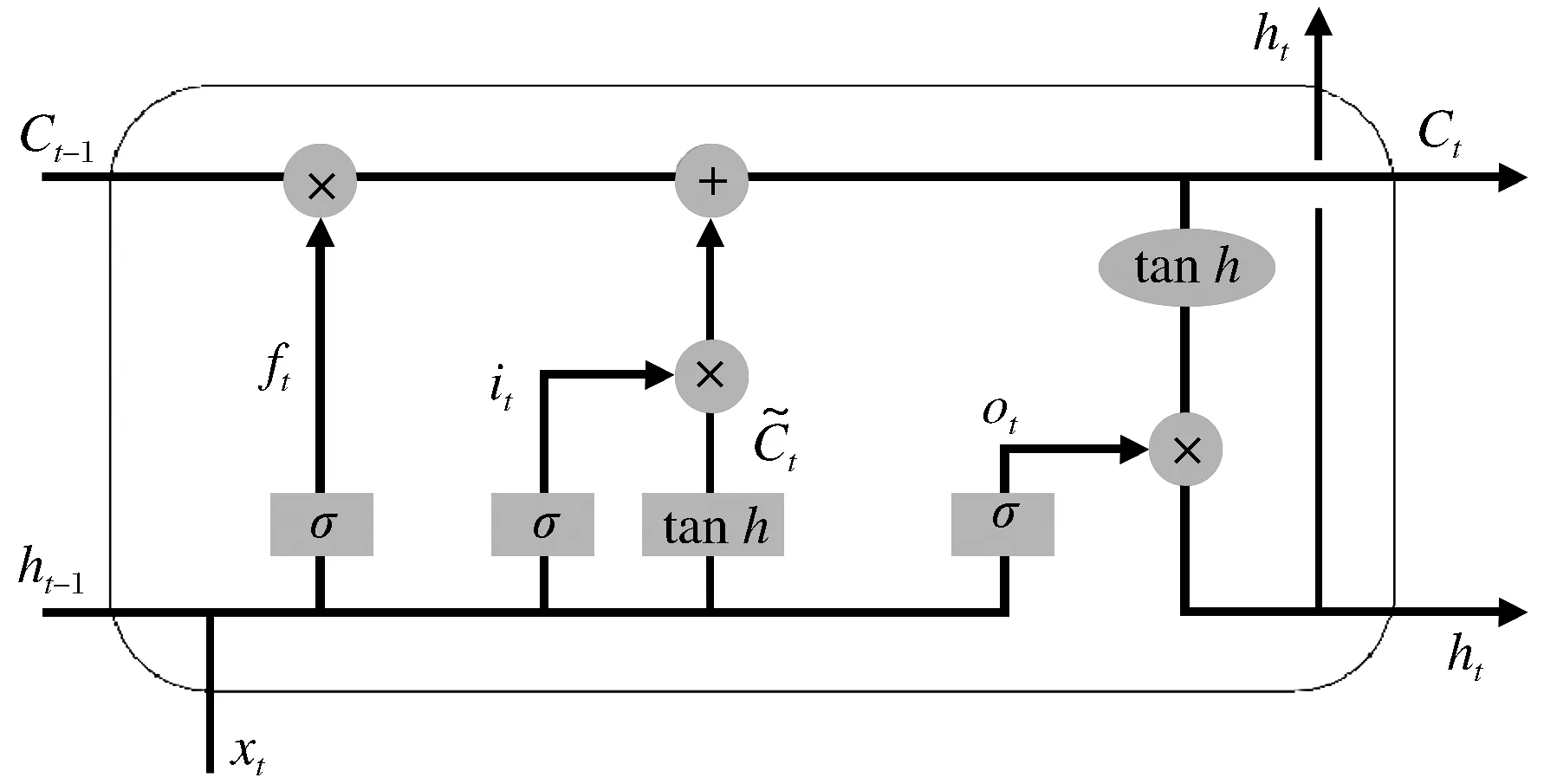
图1 LSTM神经网络单元结构Fig.1 Unit structure of LSTM neural net model

图1中xt为当前时刻的输入;ht-1和ht分别表示上一时刻和当前时刻的隐藏层状态;Ct-1和Ct为上一时刻和当前时刻的神经元状态;σ和tanh表示sigmoid和tanh激活函数,通过激活函数以及点乘运算,能够实现门控单元的选择性通过的功能,其函数表达式分别为

(4)

利用LSTM神经网络进行预测时的主要步骤包括3个部分:

(1) 数据清洗。这一过程由遗忘门实现,它决定输入的上一时刻隐藏层状态和当前时刻的实际值中什么部分应该被遗忘,通过对输入值进行加权和偏置,并通过激活函数σ计算出遗忘系数。遗忘系数的计算公式可以表示为

ft=σ(Wf·[ht-1,xt]+bf),

(5)

其中:ht-1为上一时刻隐藏层状态;xt为当前时刻实际值;ft为遗忘系数;Wf和bf分别表示遗忘门权重及偏置量。

(2) 数据更新。这一过程由输入门以及一个tanh层共同实现,它决定我们将在神经元状态中保留哪些信息。通过sigmoid层可以得到要更新的数值,通过tanh层可以求得新的候选数值,其计算公式为

(6)

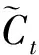
(3) 模型输出。这一过程由遗忘门、输入门以及输出门共同实现,它决定模型当前时刻的隐藏层状态、神经元状态以及预测值,其计算公式为

(7)

yt=Woht+bo,

(8)

其中:ht和Ct分别表示当前时刻的隐藏层状态、神经元状态;ot为输出控制量;Wo和bo表示输出门的权重和偏置;yt为预测值。

LSTM模型使用反向传播的方法实现误差最小化,利用梯度下降法调节各层权值,迭代减小代价函数,最终确定模型。

3 结合CEEMDAN的LSTM模型

将CEEMDAN算法与LSTM模型进行组合,利用组合模型预测滑坡监测数据的主要步骤如图2所示。

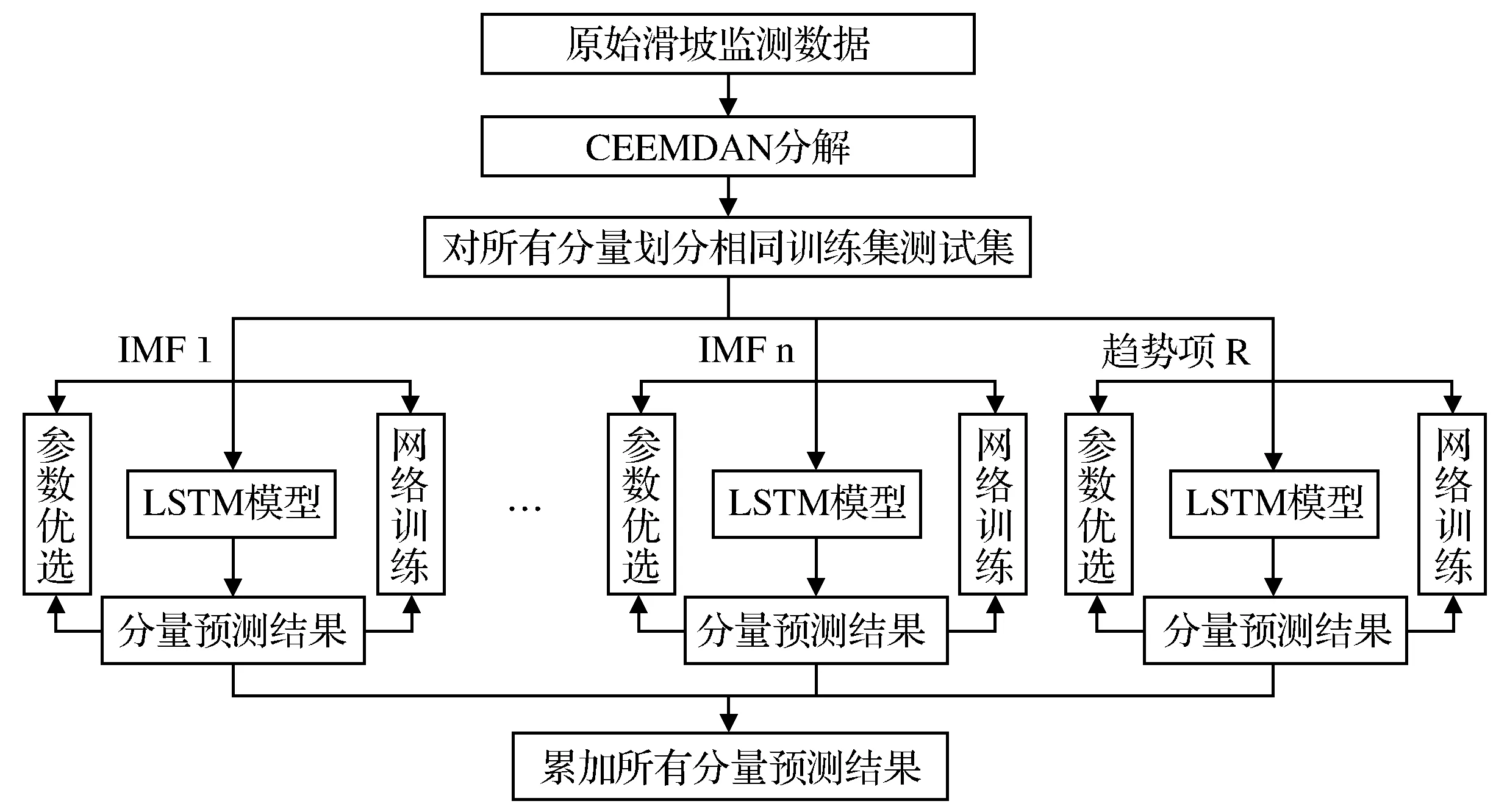
图2 组合模型预测滑坡沉降数据流程Fig.2 Flow chart of landslide settlement data predicted by combined model

图2中参数优选指采用网格搜索和交叉验证选取在LSTM模型预测中表现最优的超参数,即算法遍历训练数据集的次数epoch、一次训练所选取的样本数batch_size以及窗口分割长度等。网络训练过程是指模型损失计算以及利用Adam算法作为优化器对模型进行优化,通过每个分量理论输出以及模型输出计算得到的均方根误差来评定其预测精度。将所有分量的预测结果相加得到的结果作为组合模型对原始数据的预测结果,以预测结果和真值之间的均方根误差和相对误差作为模型总精度的评定标准。

4 计算结果及分析

实验选取位于杭兰高速公路巫奉段的一处边坡地区,该边坡位于新华夏系的第三沉降带和隆起带的交界处,坡脚较陡,坡深及坡顶较缓,其起止桩号为YK33+500、K33+900,长400 m[15]。由于该地区为亚热带季风气候,降雨量和强度都很大,大量的降雨和连续的暴雨极易引发滑坡,因此监测点变形较为明显。以其中某一监测点A1连续35期累计变形量监测数据为例进行实验,划分前30期数据为训练集进行建模,并通过最后5期数据对比分析模型的预报精度。该监测点前30期累计变形量观测数据如表1所列。

4.1 单一LSTM模型

首先利用单一LSTM模型对沉降量进行预测,选取网格搜索和交叉验证中表现最优的一组参数进行实验,此处选取算法遍历训练数据集的次数为330次,一次训练所选取的样本数为2,其预测结果如图3所示。

从图3中可以明显看出,虽然拟合曲线的趋势与原始数据非常相近,但存在较为明显的滞后现象。这种现象可能是由于时间序列数据存在自相关性,而模型倾向于将上一时刻的真实值作为下一时刻的预测值,导致两条曲线存在滞后性。与ARMA模型中的处理方法类似,想要消除这种数据的自相关性,往往是将数据进行差分处理,对差分后的数据进行预测并反推真值。经过实验发现,差分后的数据预测结果与原始数据相差很大,结果可信度大大降低。

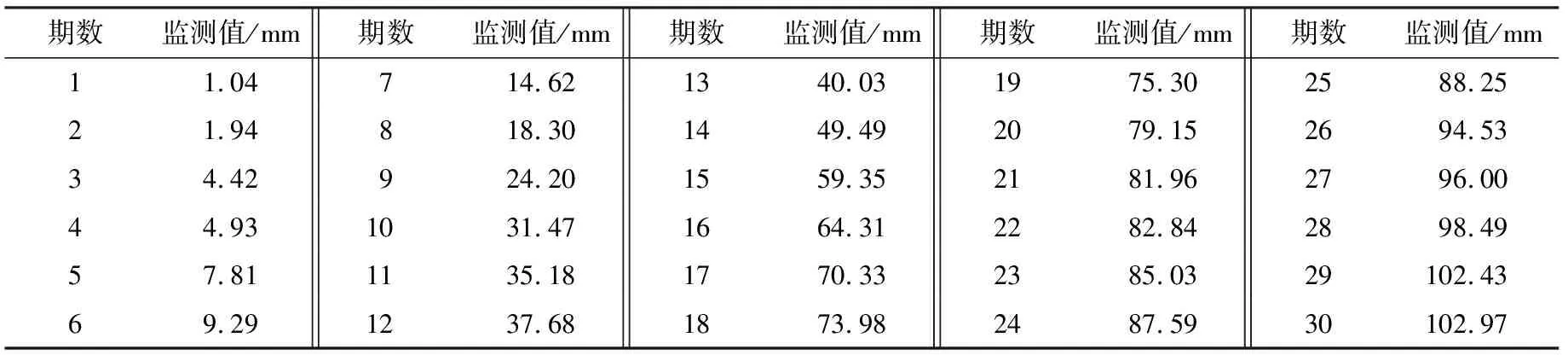
表1 监测点各期累计变形量监测值Table 1 Monitoring value of cumulative deformation in each period of monitoring point

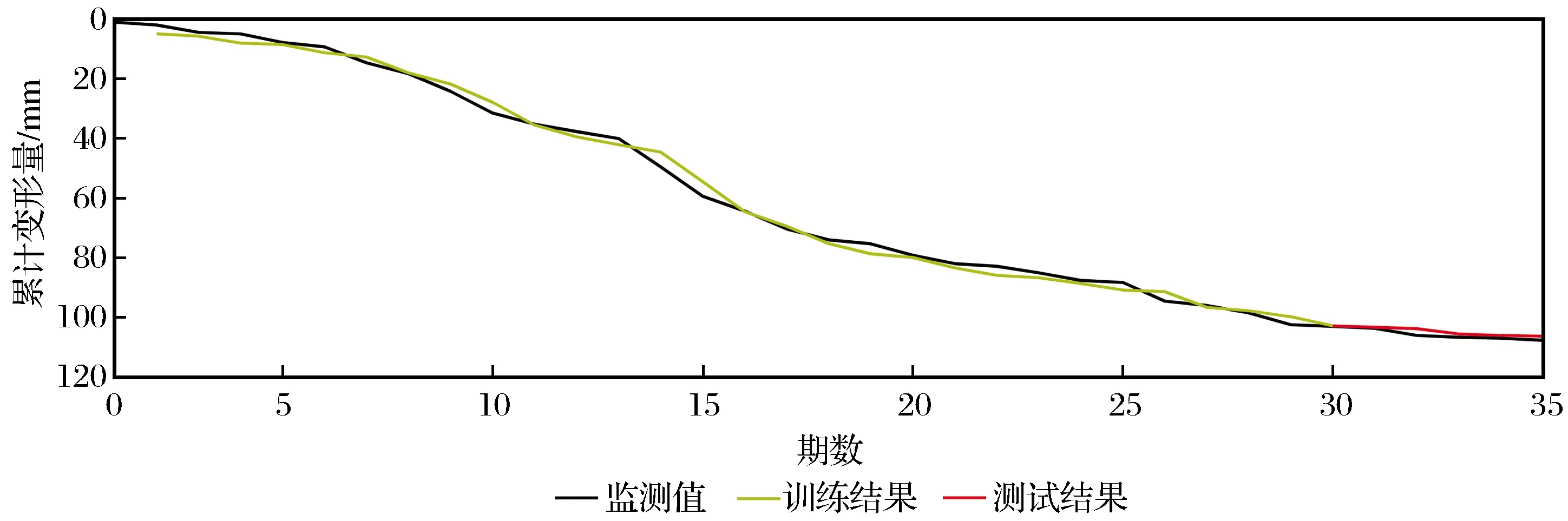
图3 单一LSTM模型预测结果Fig.3 Predicted results of single LSTM model

4.2 结合CEEMDAN的LSTM模型

首先对原始数据进行CEEMDAN分解,共得到4个IMF分量和1个趋势项,分解信号如图4所示。图4中DATA是实际监测值,IMF1～IMF4分别为4组IMF分量,R为趋势项。最下方为各分量重组时与原始数据之间的重构误差,通过计算可知在4次分解的情况下重构误差为0。

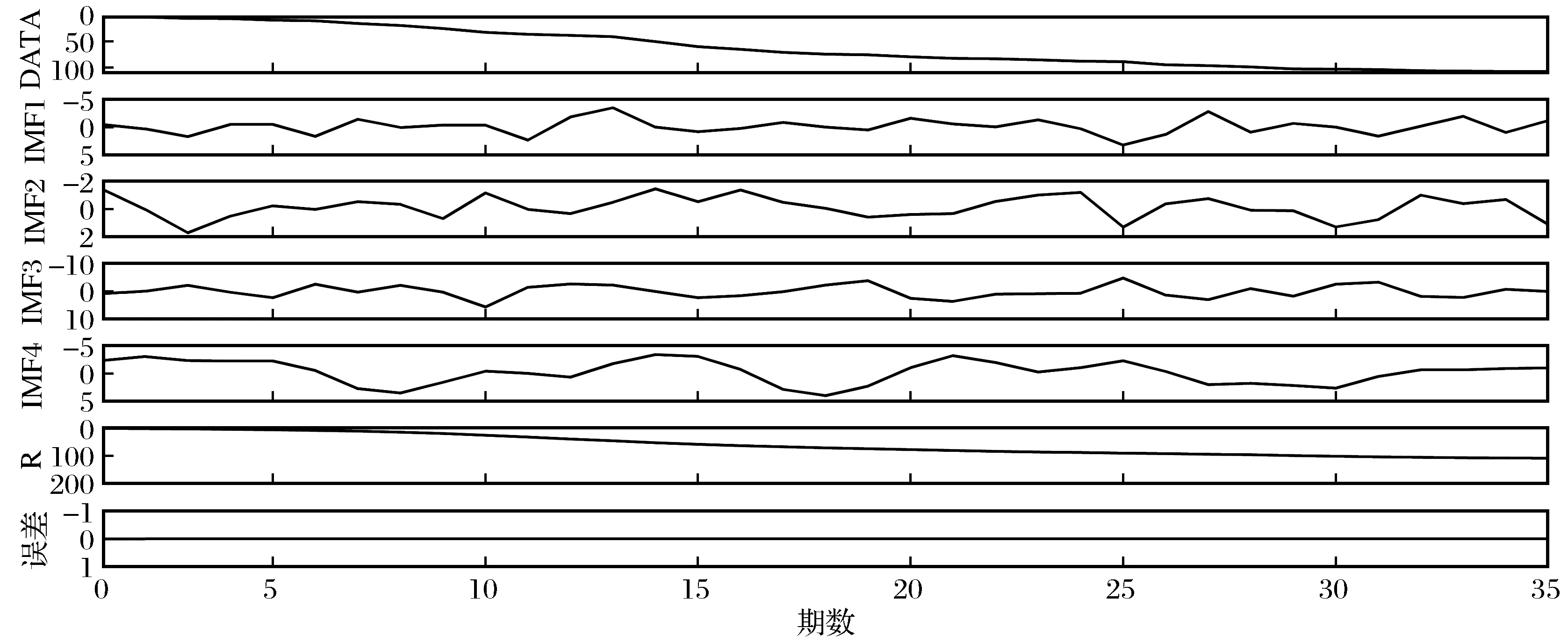
图4 CEEMDAN分解结果Fig.4 CEEMDAN decomposition results

由于在单一LSTM模型预测中出现了明显的滞后现象,分析认为其产生原因是垂直位移观测值序列具有自相关性,因此在对各个分量进行预测前首先对其进行平稳性检验。这里采用单位根(ADF)检验法,检验结果为0时认为数据非平稳,结果为1时认为数据平稳。

利用LSTM模型分别对各分量数据进行预测,分别用各分量及重构数据的训练结果、测试结果与实际值之间的均方根误差作为模型训练和测试的评定标准。误差越小,表示模型的训练和测试精度越高。训练和测试均方根误差的计算公式为

(9)

其中:Hi表示训练数据拟合结果;Ti表示模型预测值;Ai为真实值。重构数据的训练结果为各分量训练拟合结果之和,预测值为各个分量的预测值之和。平稳性检验结果及训练、测试均方根误差如表2所列。

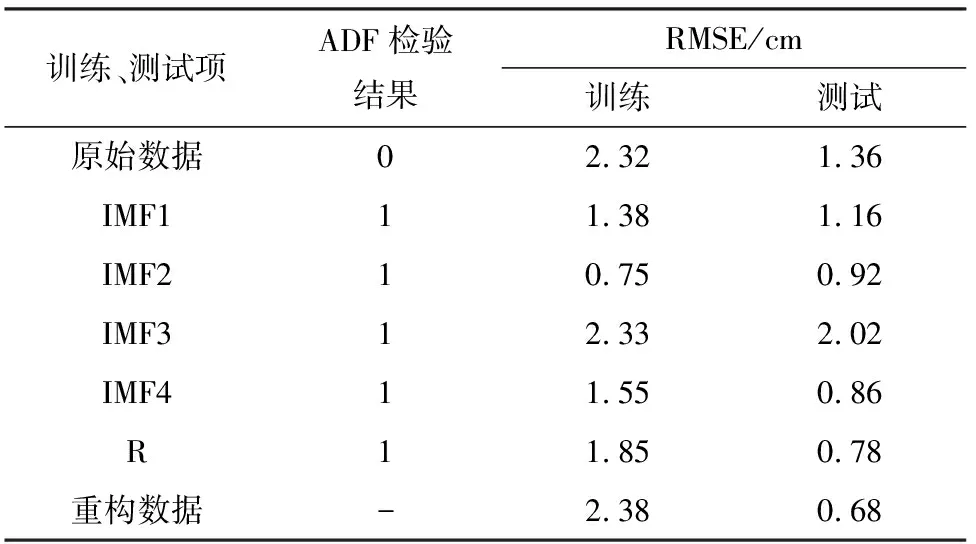
表2 平稳性检验结果及训练、测试均方根误差Table 2 Stationarity test results and RMSE of training and testing

从原始数据和各IMF分量的ADF检验结果中可以看出原始数据是非平稳数据,而CEEMDAN算法分解得到的5个分量都是平稳数据。对比训练数据和测试数据的均方根误差可知,除IMF3训练和测试误差较大外,其余每组分量的训练测试数据的均方根误差都明显小于用原始数据直接进行预测所得到的均方根误差,且重构数据的测试误差较原始数据降低近50%,即利用CEEMDAN算法分解得到各分量,分别进行LSTM模型预测并进行重构的方法能够显著提高预测精度。

4.3 不同模型对比分析

将结合CEEMDAN的LSTM模型的预测结果与单一LSTM模型、ARMA模型以及Kalman滤波模型的预测结果进行对比,分析模型在滑坡变形预报中的性能。其中ARMA模型预测结果引用文献[14]中结果。用于预测的5期数据测量值及各模型预测值如表3所列,各模型预测值与测量值之间的相对误差如表4所列。

从前3组模型预测值可以看出,对非平稳的时间序列数据进行预测时普遍存在滞后性问题,在单一LSTM模型中表现最为明显。单一LSTM滤波模型预测结果偏差最大,最大相对误差达到2.13%,但将预测值与前一时刻的测量值对照时,偏差值大大降低。其次是Kalman滤波模型,其最大相对误差为1.96%,且5期预测值之间的变化速率基本一致,即在多步预测中难以对数据趋势的改变进行精确预测。此处所用ARMA模型为多次单步预测的结果,不会产生误差的累计,相对直接多步预测来说精度更高,但其最大相对误差为1.48%,仍然高于用组合模型进行多步预测的误差。

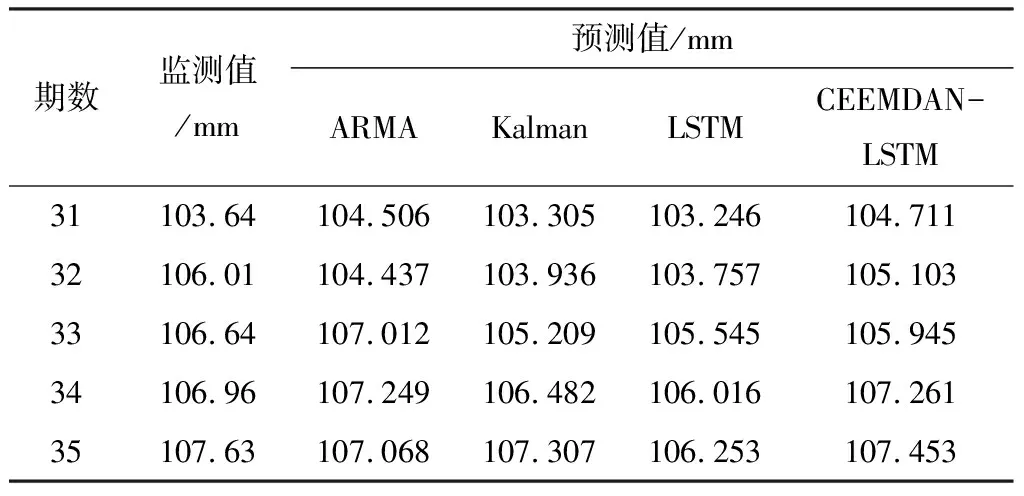
表3 监测值与预测值对照

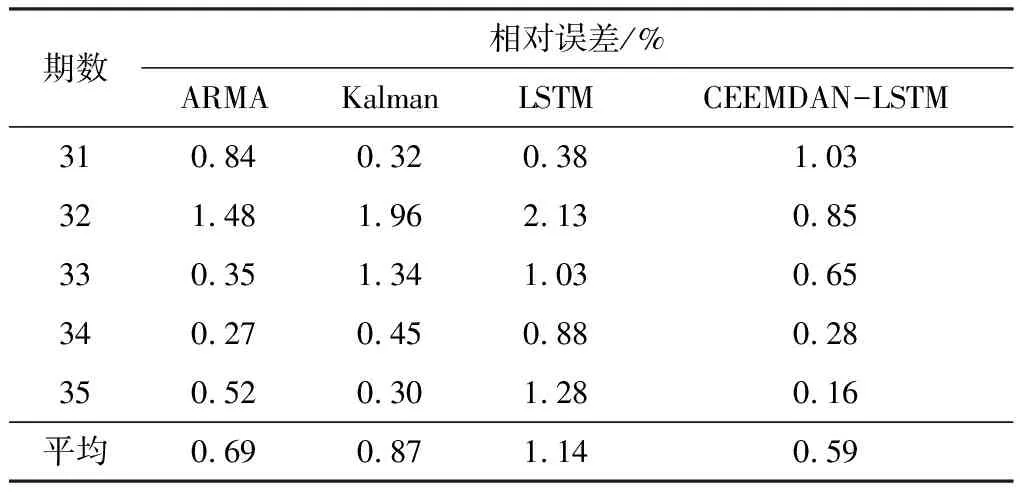
表4 各模型预测值与测量值相对误差

与其他3个模型相比,结合CEEMDAN的LSTM模型不仅解决了滞后性问题,能够清晰预测出监测数据的变化趋势,且预测结果与实际值的偏差明显小于其他3个模型,最大偏差不超过2 mm,相对误差基本在1%以内,平均相对误差为0.59%,预测精度大大提高。

5 结论

为研究神经网络模型在变形预测中的效果,选取位于杭兰高速公路巫奉段的一处边坡地区的一个监测点的变形监测数据进行实验,将结合CEEMDAN的LSTM模型的预测结果与单一LSTM模型、ARMA模型以及Kalman滤波模型的预测结果进行对比,结论如下:

(1) 对滑坡变形数据进行CEEMDAN分解后能够得到平稳的模态分量,利用LSTM模型对这些模态分量进行预报,能够解决使用单一LSTM模型时由于时间序列数据的自相关性引发的滞后性问题。

(2) 组合模型的预测结果能够较好地体现数据的变化趋势,其多步预测结果精度明显高于使用单一LSTM模型、Kalman滤波模型进行多步预测的结果,略高于使用ARMA模型进行多次单步预测的结果。

(3) 将结合CEEMDAN的LSTM模型用在滑坡变形预报中,其预测值与测量值的偏差均在2 mm以内,平均相对误差为0.59%,模型预测效果较好。