对存在缺失的二项数据的第一阶段监控

李 静,贾玉洁

(天津大学管理与经济学部,天津 300072)

随着科技的进步,产业技术也在不断地升级换代。在提高生产力的同时,必然要求提高对生产过程中非随机性因素监控的效率,从而不断降低生产过程波动以达到改善产品质量的目的。统计过程控制(SPC,statistical process control)是质量控制的重要技术手段,它被广泛应用于生产制造、医疗健康、物流供应链管理以及企业管理等领域的质量管理和控制。统计过程控制通常分为2个阶段:阶段Ⅰ(Phase Ⅰ)的主要目标是检验历史数据是否受控,去除不稳定的数据,并用受控数据估计过程参数,较为准确地把握过程;阶段Ⅱ(Phase Ⅱ)的主要任务是收集生产过程中的实时数据,并据此构造控制图,对过程进行监控。

在现代制造过程中,同时监控2个或多个质量特性比监控单一的质量特性更为常见。此时需要考虑多变量的控制图。在过去的几十年人们提出了一些多元控制图,如T2控制图[1-2]、多元累计和(MCUSUM,multivariate cumulative sum)控制图[3-4]、多元指数加权移动平均(MEWMA,multivariate exponent weighted moving average)控制图[5-6]等。以上研究大都关注多变量的正态数据,相较而言,对于多变量的属性数据监控的研究比较少。Topalidou等[7]对多项和多属性控制图进行了回顾;Chiu等[8]提出了一个新的控制图来监控二元二项过程;Kamranrad等[9]基于广义线性检验为列联表和多元分类变量在阶段Ⅱ的监控提供了新的框架;Shang等[10]基于广义线性回归(GLM,generalised linear regression)模型提出了可以监控二元二项数据的新似然比控制图。更多关于属性数据监控的研究,可以参阅Montgomery[11]的研究。

实践中由于不同的原因,在阶段Ⅰ和阶段Ⅱ的数据集中都可能出现一些缺失值,而且在阶段Ⅰ的数据集中存在缺失的值比在阶段Ⅱ的影响更严重。这是因为如果历史数据中的缺失值得不到准确处理,会影响过程参数的估计,进而导致在阶段Ⅰ错误判断受控和失控样本,从而影响控制图在阶段Ⅱ的性能[12]。缺失数据的特征和影响在统计领域已得到全面讨论,学者们[13-5]也提出了各种处理技术。

此外,部分研究关注了过程监控中数据存在缺失值的问题,如Wilson[16]通过调整EWMA控制图的权重,克服了阶段Ⅱ监控中出现的缺失观测值的问题;Waterhouse等[17]通过比较平均运行长度(ARL,average run length),研究了3种用于处理缺失值的方法对3种不同的多元控制图性能的影响,并建议在数据缺失严重时采用多重插补来创建完整的数据集;Madbuly等[18]研究了用于处理缺失值的5种方法对多元EWMA控制图在阶段Ⅱ的性能的影响;Mahmoud等[12]讨论了4种插补方法对T2控制图在阶段Ⅰ性能的影响;Mahmood等[19]采用T2控制图来监视医疗应用中的不完整数据;He等[20]基于广义估参方程(GEE,generalised estimating equation)研究了随机及不平衡设计下的阶段Ⅰ自相关泊松轮廓的监控问题。

然而,鲜有研究关注存在缺失的多变量二项数据的监控问题。现实中我们需要控制不同批次产品的次品率,通常不同批次产品的数量及次品率是不同的,这是一个针对多变量的二项数据的监控问题。数据缺失在现实管理中在所难免,鉴于在阶段Ⅰ的数据集中存在缺失值比在阶段Ⅱ的影响更严重,研究考虑存在缺失的多变量二项数据在阶段Ⅰ的监控。研究不同程度的缺失对T2控制图的影响,采用均值插补(MS,mean substitution)、线性回归插补(RG,regression imputation)、随机线性回归插补(SRG,stochastic regression imputation)和多重插补(MI,multiple imputation)来创建完整数据集。

1 缺失数据处理方法

在纵向数据研究中经常会发生数据缺失现象[21]。对于数据缺失问题需要明确两点:一是数据缺失机制,二是缺失数据分布模式。Little等[13]将数据缺失机制分为了3种,分别是完全随机缺失、随机缺失和非随机缺失。其中完全随机缺失是指数据缺失的发生与观测值和缺失值都无关;随机缺失是指数据缺失的发生与缺失值无关,但与观测值有关;非随机缺失是指数据缺失的发生与缺失值有关。常见的缺失数据的分布模式有间歇式和退出式,间歇式数据缺失是指样本发生数据缺失后仍可能会回到实验中来;退出式数据缺失是指某个位置发生缺失后再也没有对应观测值。考虑最常见的数据缺失情况,即数据缺失可能会发生在任意样本的任意位置,假设数据缺失机制为完全随机缺失。对缺失数据的处理方式主要分为2种:样本删除和数据插补。先前研究已证明只考虑具有完整数据的样本会造成信息损失,而将插值和控制图结合使用能有效提高控制图的监控性能[12,18]。故考虑采用以下插值方式来得到完整数据集。

1.1 均值插补(MS)

1.2 线性回归插补(RG)

线性回归插补是指对变量进行线性回归分析,再基于回归模型预测缺失值。与均值插补使用无条件均值不同,线性回归插补采用的是有条件均值,故线性回归插补也被看作是对均值插补方法的优化。在Buck[22]的研究中,只有具有完整观测值的样本才会被纳入回归分析的范围,但此法并不可行,因为当数据缺失率较高时,无法保证足够完整的样本供回归分析。另一种处理方式由Chan等[23]提出,即使用所有数据来进行回归模型拟合。具体而言,就是先对样本进行均值插补从而得到伪完整数据集,再基于此数据集为每个变量分别建立回归模型,最后根据伪完整数据集及各回归模型产生各缺失观测的预测值。由此方法产生的数据集的均值可作为实际均值的有效估计量。但线性回归插补存在的数据过拟合问题会导致样本协方差值的增加。

1.3 随机线性回归插补(SRG)

为了克服线性回归插补的数据过拟合问题,Madbuly等[18]和Mahmoud等[12]建议为缺失数据的预测值增加随机误差项ε,ε服从均值为0,方差为回归模型的均方误差的正态分布。当数据缺失机制为完全随机缺失或随机缺失时,基于随机线性回归插补产生的数据集的均值估计为原均值的一致估计量[15]。

1.4 多重插补(MI)

均值插补、线性回归插补和随机线性回归插补都属于单一插补的范畴,另一种插补类型是多重插补。多重插补是指对各缺失位置产生多个候选预测值,再将这些候选值汇总,最终得到各目标位置的单值估计。在模拟次数的选择上,Ae等[24]指出迭代3～10次即可。此处选定的迭代次数M=10。

多重插补的具体步骤如下:

(3)t=M则迭代结束,将以上生成的M个数据集取平均值形成一个数据集。

值得注意的是,通过以上插值方法产生的预测值,需要四舍五入。且当预测值小于0时,取0值,以与各变量服从二项分布的假设保持一致。

2 T2控制图的建立

假设有一个包含m个样本的数据集,对于i=1,2,…,m,xi=(xi1,…,xip)为代表样本观测值的一个 (p×1) 维向量。首先,基于连续差值的统计量[12],即

vi=xi+1-xi,i=1,2,…,m-1

将vi聚合成矩阵V。考虑到过程监控的主要目的是监测样本值的非随机波动,故T2统计量可以表示为

3 仿真性能及评价

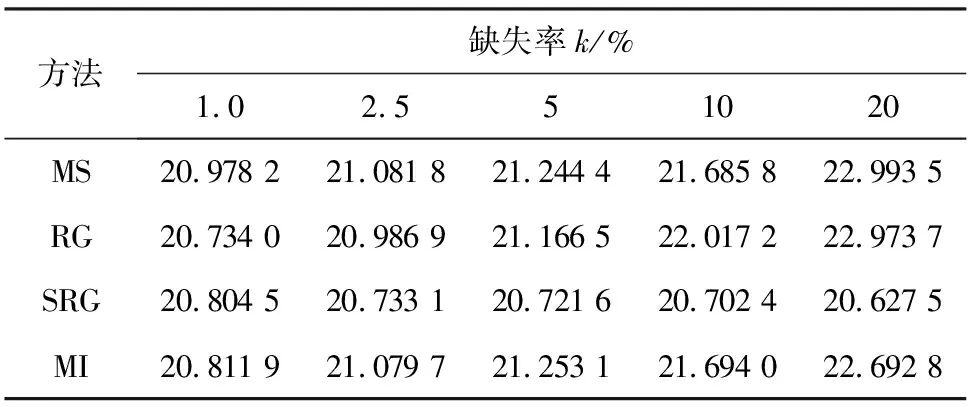
表1 不同缺失率及插值方法下的T2控制图临界值

此处考虑3种不同变点位置,即τ取10、25、40。假设τ时刻之后的样本参数π发生了偏移。对于τ取不同值的情形,各插值方法处理后数据集的发出失控信号的概率如表2～表4所列,表中k=0是指数据为完整数据的情况。由表2和表3可知,当失控样本数量较多时(τ=10,25),对于较低的缺失率(k≤2.5%)的情况,RG的性能最优,MS和MI分别在k=1%及k=2.5%时表现最差;当k=5%时,RG和MS分别在偏移程度低和偏移程度高时表现最好,SRG和MI分别在偏移程度低和偏移程度高时表现最差;当缺失率(k≥10%)时,效果最好的是MS,RG和SRG分别在k=10%及k=20%时表现最不理想。由表4可知,失控样本数量较少(τ=40)时,4种插值方法的表现也和失控样本数量较多(τ=10,25)时结果类似,不同的是缺失率k=2.5%及k=10%时效果最差的由RG变成了SRG。整体上RG在低缺失率时表现最好,MS在中等及高缺失率时效果最佳,SRG和MI始终表现一般。但当失控样本数量较少时,SRG的表现还会劣于MI。

表2 τ=10时T2控制图的发出信号概率

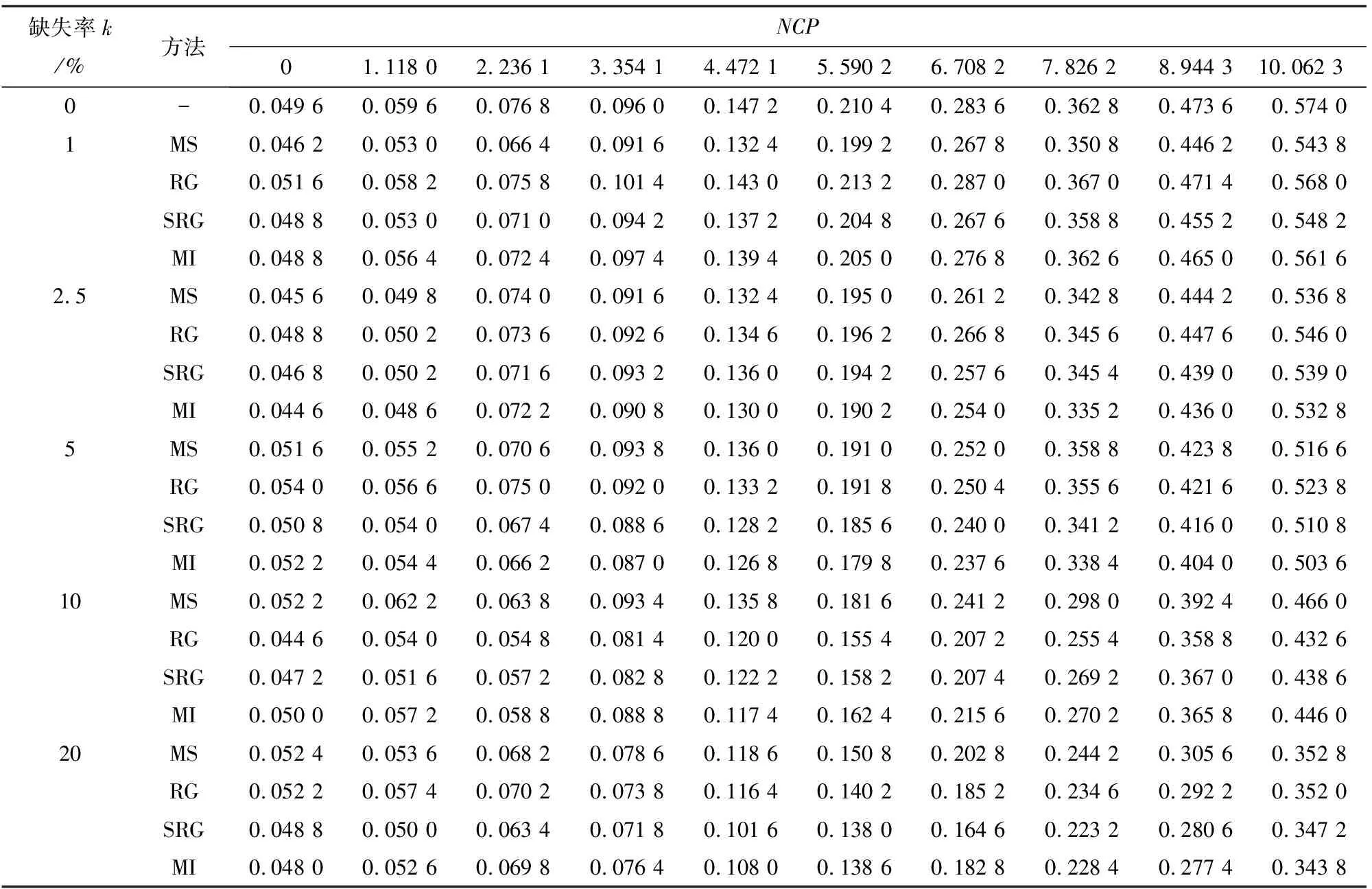
表3 τ=25时T2控制图的发出信号概率

表4 τ=40时T2控制图的发出信号概率

4 结论

通过比较4种插值方法下T2控制图在第Ⅰ阶段监控缺失数据时的性能,以整体发出失控信号概率为衡量标准,考虑了3种偏移发生的位置和5种缺失比例。研究发现在低缺失率情形采用线性回归插补对数据进行插补,在中高缺失率情形采用均值插补对数据进行插补,可以提高T2控制图的监控性能。仿真结果表明基于插补的完整数据集,控制图能有效地对缺失数据进行监控。虽然以上插值方法通常针对连续数据,但推广到二项分布的情形也取得了良好的插值效果,为后续对各类缺失数据的统计过程控制研究提供了思路。