具有颜色恒常性的光谱反射率重建

姜丹阳，王智峰*，高 程, 2，李长军

1. 辽宁科技大学计算机与软件工程学院，辽宁 鞍山 114051 2. 辽宁科技大学电子与信息工程学院，辽宁 鞍山 114051

引 言

人类视觉系统中对颜色的感知取决于人眼视锥细胞，光照以及物体反射率等许多因素。 但是不管场景中光照以及物体表面的反射率如何变化，人类都有一种对特定物体本身颜色识别一致性的心理倾向，这种心理倾向就是颜色恒常性[1]。 如何在重建物体光谱反射率时考虑到颜色恒常性问题，使物体在不同的光源下具有相近的颜色感受，在颜色复现领域是一个重要的研究方向，也是纺织、印染、涂料、油漆等行业面临的难题。 目前常见的光谱反射率重建方法是利用已知光源下的三刺激值或RGB数据进行重建，如维纳估计方法[2]或主成分分析方法[3]，通过训练样本获得物体三刺激值到反射率的映射矩阵以重建反射率。 或者如Cao等提出的通过使用最小色差对训练样本进行选取并加权重建反射率的方法[4]。 这些方法都着重于重建精度，没有考虑到重建出反射率的颜色恒常性。

针对如何重建出具有颜色恒常性的反射率问题，过去的研究者提出一系列利用线性规划算法的解决方案。 如Takahama和Nayatani提出了一种将不同光源下三刺激值的曼哈顿距离作为线性规划目标函数的反射率重建方法(以下称为Takahama方法)。 之后Berns和Billmeyer等又提出了一种在重建反射率过程中通过使用色相角对颜色恒常性进行约束的方法(以下称为Berns方法)。 此后，Li和Luo对前两种方法进行改进，使用改进的色适应变换CAT02，提出一种基于二次规划的重建方法，得到更加具有颜色恒常性的光谱反射率(以下称为Li方法)[5]。 以上三种基于线性规划或二次规划的方法在提高光谱反射率的颜色恒常性上有一定效果，但是测试结果发现所有方法重建的反射率所对应的颜色变换指数较原来的反射率所对应的变换指数可能要高，这不是人们所期望的。 本文基于给定的在参考光源下三刺激值，提出以颜色变换指数和光滑性约束的组合作为非线性规划的目标函数，以重建的反射率在参考光源下的三刺激值作为等约束条件的非线性约束优化问题重建反射率。 测试结果表明本文所提出的方法要优于Li，Berns和Takahama方法。

1 颜色变换指数

颜色变换指数用于衡量光谱反射率在不同光照条件下的稳定程度。 使用ISO标准计算方法CMCCON02[6]作为评判光谱反射率颜色恒常性的指标，并将CMCCON02使用的色适应变换CAT02替换为色适应变换CAT16[7]。 前者提出于2002年，嵌入在CIE 2002色貌模型CIECAM02[8]中，后者提出于2016年，在色适应变换的精确性，可用性等方面能够持平或者优于CAT02，是近些年被提出替代CAT02的色适应变换方法。 图1给出了颜色变换指数的计算步骤。 第一步： 计算出反射率r(列向量)在第j(j=1, …,n)个测试光源和参考光源R下的三刺激值，分别构成列向量pj和pR。 第二步： 通过CAT16计算出在参考光源R下与pj有相同色貌的三刺激值列向量pC。 第三步： 计算pR与pC的CIELAB2000[9]色差ΔE00，ΔE00即为颜色变换指数(color inconstancy index, CII)。

图1 CMCCON02计算步骤Fig.1 Procedure for computing the CMCCON02

2 实验部分

对于给定在参考光源下的三刺激值pR，提出了一种具有颜色恒常性的光谱反射率重建方法，该方法将CII加入到非线性规划的目标函数中，以重建出具有颜色恒常性的光谱反射率。 首先，令M为计算三刺激值的加权表矩阵，仅依赖于光源光谱和颜色匹配函数，MR和Mj分别作为参考光源和第j个光源下的加权表矩阵。 那么重建后的反射率r需要满足

pR=(MR)Tr

(1)

式(1)中，上标T是矩阵或向量的转置。 计算反射率r在测试光源j(j=1, …,n)下的三刺激值pj(j=1, …,n)，并通过CAT16将pj转换为参考光源下对应色的三刺激值pC, j，该转换公式为

pC, j=Ujpj=Uj(Mj)Tr

(2)

式(2)中，Uj是将CAT16计算过程简化得到的一个3×3矩阵，它取决于参考光源三刺激值、测试光源三刺激值。 本文使用的CII计算方法为

CIIj=ΔE00(pR,pC, j),j=1, 2, …,n

(3)

式(3)中，ΔE00(pR,pC, j)为物体在参考光源下三刺激值pR与参考光源下的对应色pC, j的CIELAB2000色差。 假定有n个测试光源，则整体颜色变换指数CII为

(4)

此外，研究发现自然颜色反射率通常趋于光滑[10]，所以为了保证重建出的反射率具有光滑性，本文通过在非线性规划的目标函数中引入对角矩阵G与光滑因子s，确保重建反射率的光滑性。 由此，可以导出以下非线性约束规划问题

Minimise CII+s‖Gr‖2

Subject to: 0≤r≤1, andpR=(MR)Tr

(5)

式(5)中，s是一个权重值，它的大小决定了重建出反射率的光滑性，也影响了重建反射率的颜色变换指数CII，并且，反射率r的每个分量都属于[0, 1]区间。

3 结果与讨论

实验在MATLAB平台进行，非线性规划算法使用MATLAB内置函数fmincon，其options变量设置使用默认参数。 重建出反射率r的波长范围为400～700 nm之间，并以10 nm为间隔取值的31×1的向量。 其他数据如加权表，光谱功率分布和CIE1964颜色匹配函数等都在此范围内取值。

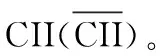
图2 不同光滑权重对反射率重建过程中颜色恒常性的影响

图3中，Berns方法产生的光谱反射率光滑性尚可，但是起伏波动过大，出现了较多的极值点。 Takahama方法产生的光谱反射率曲线与原始反射率相比有着大致相同的变化趋势，但曲线呈现出阶梯状。 本文方法重建反射率光滑性约束与Li方法相同，重建出优于其他两种方法的光滑曲线。

表1给出利用Munsell色卡数据集进行测试的平均和最大CII，重建和原始反射率的平均和最大均方根误差(root mean squared error，RMSE)，以及平均和最小拟合优度系数(goodness of fit coefficient, GFC)，其中RMSE值越小重建精度越高，GFC的最大值为1，并且其越接近1重建反射率的拟合程度越好。 表1中黑体数字表明，按该指标(所在列)对应的方法(所在行)表现最好。 首先可以看出本文方法对应的CII指标，不论是按平均还是最大颜色恒常指标，都要好于其他方法；然后预测的反射率与原反射率接近程度指标RMSE与GFC一共包括平均和最大RMSE与平均和最小GFC四项。 Li方法的平均RMSE和平均GFC指标最好，而本文方法在最大RMSE和最小GFC指标最好。 因此，在预测的反射率与原反射率接近程度评价指标RMSE与GFC中，本文方法和Li方法表现最好，其次是Takahama方法，最差的是Berns方法。

图3 不同方法重建反射率Fig.3 Spectral reflectance reconstruction of different methods

表1 不同方法重建反射率结果对比Table 1 Comparison of reflectance reconstruction results by different methods

图4给出了原始反射率的颜色变换指数(横轴)和每种方法重建的反射率的颜色变换指数(纵轴)比较。 图中红线是斜率为1的直线，每一个圆点代表一个标准Munsell色卡，黄线为所有圆点的线性回归方程。 当重建后的反射率的CII与原始反射率的CII相同时圆点应该与红线相交，重建反射率的CII小于原始反射率的CII时圆点落在红线下方，将其称为正优化，否则称为负优化。 且重建反射率的CII越多小于原始反射率时，黄线与x轴的夹角则越小。 由此可见，本方法重建1 560组反射率得到的黄色线段斜率最小，且重建反射率的CII中全部好于原始反射率的CII，而Li方法、Berns方法和Takahama方法在重建反射率过程中会出现大量负优化情况。 本方法整体优化的趋势上要远远好于其他三种方法。

图4 反射率的颜色变换指数(横轴)和重建反射率对应颜色变换指数(纵轴)(a)： 本文方法; (b): Li方法; (c): Berns方法; (d): Takahama方法Fig.4 CII for original reflectance (horizontal axis) versus CII for reconstructed reflectance (vertical axis) based on Munsell dataset(a)： The proposed; (b): Li; (c): Berns; (d)： Takahama

需要说明的是以上结果本文方法采用光滑权重s=6，当s>6时，重建的反射率要更接近原始反射率，但可能会出现一定量的负优化，如s=15时，测试结果表明有2%的负优化出现，但重建的反射率与原始反射率的接近程度要明显优于Li，Berns和Takahama方法。

4 结 论

基于给定的三刺激值重建反射率在颜色复现领域有着重要应用。 目前常见的重建算法，常是以重建的反射率与测量反射率的接近程度为评价标准，并不保证重建的反射率具有良好的颜色恒常性。 然而在纺织、印染、油漆等应用领域，颜色恒常性是一个重要指标。 本文提出非线性约束优化方法重建物体反射率，目标函数为颜色变换指数与重建反射率具有光滑性的组合形式，因此保证了重建的反射率在具有较好的颜色变换指数的同时又具有光滑性。 比较结果表明，本文的方法，不仅就颜色恒常指标而言明显优于Li，Berns和Takahama方法，同时就接近原始反射率的指标RMSE和GFC而言也优于Berns方法和Takahama方法。 因此，本文方法对颜色复现过程中具有颜色恒常性要求的行业有着重要应用价值。