智慧课堂彰显教学智慧
——《轴对称图形》的教学实践与思考
安徽省合肥市第四十六中学南校区 薛明浩 王 菲 陈方勇 (邮编:230092)
智慧课堂是教育教学和现代化信息技术的融合,在教学过程中运用信息化手段,能够寓学于乐、寓学于趣,在发挥学生主体作用的同时,能够提高课堂教学效率,彰显教学智慧.下面以沪科版八年级上册《15.1 轴对称图形》为例,谈谈智慧课堂在教育教学中的具体实践和思考.
1 课堂教学实录
1.1 观察与猜想
教师:同学们好.前段时间,老师去了坐落在巢湖之畔的渡江战役纪念馆.这是为了纪念1949 年渡江战役的胜利、缅怀革命先烈而设计建造的.(课件呈现图片)设计师精心设计的建筑有其革命寓意,感兴趣的同学可以课下查阅了解.今天,老师带领大家用数学的眼光来观察与分析,我们将其抽象地看成平面图形(课件呈现建筑轮廓),这些平面图形有什么共同点?

学生:它们是对称的.
教师:是的,它们的对称性有什么特点呢?
学生1:它们左右两部分是一样的.
教师:我们通过观察,猜想这些平面图形是有这样的特征,怎么验证我们的猜想呢?
教学说明:
《轴对称图形》一节的引入,旨在引导学生用数学的眼光观察世界.选取当地红色革命纪念馆作为素材和楔子,在贴近生活的同时,激发学生的兴趣;对于建筑所蕴含的革命寓意的介绍设置悬念,在渗透爱国主义教育的同时,为学生课下自己查阅资料、了解史实埋下种子;结合多媒体,引导学生将现实的立体图形抽象为平面图形,进而猜想这些平面图形的特征,帮助学生经历观察-猜想的思维过程.
1.2 操作与验证
教师:老师将这些建筑的轮廓描绘并打印了出来(展示手中的纸片),同学们动手尝试操作,验证自己观察的猜想是否正确,也请大家来说一说自己是怎么操作的、发现了什么?
学生2:(展示操作)我将纸片对折后,发现左右两边能完全重合.
教师:很好!我们把符合这一类特征的平面图形,称作轴对称图形.(板书标题)大家能够结合自己的操作,说说轴对称图形的定义吗?
学生3:将纸片对折后,左右两边能够重合的图形是轴对称图形.
教师:我们是将现实中的图形抽象来看,我们主要研究的是什么图形?
学生3:平面图形,将一个平面图形对折后,左右两边能够完全重合的图形,是轴对称图形.
教师:一定是“左右两边”吗?(将纸片横放),此时还是左右两边重合吗?
学生4:应该是沿着直线折叠,直线两边的部分能够重合.
教师:很好!部分重合、部分不重合可以吗?
学生4:要全部重合.
教师:你认为,描述一个图形是轴对称图形,有哪些关键词?尝试着发表你的观点.(教师利用智慧课堂,向学生采集观点)

教师:通过收集大家的观点,我们可以看到,大家在描述一个图形的轴对称图形时,关键词集中在“对折”“折叠”“完全重合”上.我们说,如果一个平面图形沿着一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
教学说明:
在设置本环节时,旨在引导学生经历操作-验证的探究过程,在实践操作过程中感悟轴对称图形的特征,结合智慧课堂,给每位学生发表观点的体验;利用智慧课堂收集全部同学的观点,将高频观点突出呈现,帮助学生明确轴对称图形的主要特征,进而尝试用自己的语言总结概括出轴对称图形的概念,给学生自主尝试并用语言概括的机会,培养、锻炼学生用数学语言描述世界的能力.
1.3 实践应用之分类
教师:观察下列图标,哪些是轴对称图形,哪些不是?将其拖动到各自的小屋里进行分类.(将课件从教师端发送到学生平板,学生在平板上自主操作分类)

教师:老师这边已经接收到同学们的练习反馈,大家的正确率都很高,对于轴对称图形的认识很到位.

教学说明:
高质量的课堂教学应该在学生生动活泼地学习知识的过程中发展学生的核心素养、提高学生的学习成绩.[1]在设计本环节的教学内容时,从生活中的图标、文字、数字、字母等图形入手,精心挑选具有代表性的6 组提供给学生辨别并加以归纳,帮助学生一通百通,在课堂活动中熟练掌握该知识点,减轻学生课后学习负担.
在课堂教学中,结合智慧课堂的信息技术,设置分组归纳游戏,将课件通过教师端发送给每一位学生的平板,使得每一位学生都经历了动手操作、实践练习的过程,同时接收每位学生的练习反馈,准确了解每一位学生的掌握情况.
1.4 再探:数学中常见的轴对称图形
教师:生活中还有哪些物体,可以抽象地看成轴对称图形?
学生8:教室里的桌子.
教师:我们说的轴对称图形,更多的是研究平面图形,而桌子是立体图形,我们该怎么描述会更准确?
学生8:桌面,可以近似看成长方形,是轴对称图形.
教师:非常好!
学生9:教室里挂的钟,它的轮廓是圆形,是轴对称图形.
教师:非常严谨!除去我们教室内存在的一些轴对称图形,生活中、自然界还有哪些物体可以抽象地看作是轴对称图形?
学生10:蜻蜓、蝴蝶、树叶.
教师:生活中,有很多物体可以抽象看成轴对称图形,其中不乏有我们数学中很常见的几何图形,如桌面近似看成长方形,时钟近似看成是圆形等.再看我们在课前一起欣赏的渡江战役纪念馆的图片,你能发现其中的轴对称图形吗?
学生11:正方形,长方形.
教师:像圆形、正方形、长方形等,是数学中常见的几何图形,它们也是轴对称图形.同学们能动手操作,尝试剪出一个数学中常见的轴对称图形吗?给大家3 分钟的时间,大家动手做一做.(教师端显示倒计时3 分钟)
学生:剪纸操作.
教师:老师观察到,有一些学生剪的是圆形,但是有不同的剪法,请两位同学分别来说一说自己是怎么剪出圆形的.
学生12:我是用圆规,在纸上画出了一个圆,再将这个圆剪了下来.
学生13:老师,我是将纸对折了一下,然后用圆规画了一个半圆,将这个半圆剪了下来,展开得到了一个圆形.
教师:两位同学都用自己的方法剪出了圆形.请你来介绍一下,为什么要对折再剪呢?
学生13:我想的是,圆是轴对称图形,它对折后两边完全重合,我将一张纸对折后,剪一个半圆出来,展开就是一个圆形了.
教师:想法非常好!轴对称图形的定义告诉我们,将一个平面图形沿着一条直线折叠后,直线两旁的部分能够完全重合.那我们反过来思考,要得到一个轴对称图形,只要沿着一条直线折叠后剪出图形的一半,展开后就能得到完整的轴对称图形.我们在实际操作的过程中,将一张纸对折后再裁剪,能够事半功倍.
教师:大家还有没有剪出其他的几何图形?可以展示一下.
学生14:我剪出的是一个等腰三角形.
学生15:我剪的是长方形.
教师:大家做得很好!像等腰三角形、长方形、圆形、正方形等,是数学中常见的几何图形,更是轴对称图形.(展示课件)大家看看老师手中的这样一个一般的平行四边形,它是轴对称图形吗?为什么?
学生16:不是的,它没有办法通过折叠,两边完全重合.
教师:那么对于等腰三角形、正方形、圆形这些轴对称图形,你能画出它们的对称轴吗?(教师将课件推送至学生平板,学生在课件上利用虚拟尺规画图,教师得到反馈结果)
教师:大家都做得很好!我看到大家很细心,在画对称轴时,都是用直线和虚线.这些图形的对称轴各有几条呢?
学生17:等腰三角形有一条对称轴,正方形有四条,圆形有无数条对称轴.
教师:对于轴对称图形,大家能总结一下,它的对称轴的条数,有何特点吗?
学生18:一个轴对称图形,可能有一条对称轴,可能有四条,也可能有无数条对称轴.
学生17:轴对称图形,至少有一条对称轴.
教师:很好!那么对于下面两个轴对称图形,大家能画出它们的对称轴吗?在老师给大家发的课堂任务清单里,自己动手画一画.

学生完成后拍照上传,教师端汇总每一份课堂任务反馈,教师选取具有代表性的作业展示、点评.
教学说明:
真正高质量的知识教学,需要在学生的经验和抽象的知识之间建立起联系,让学生觉得,原来“考点”并不只出现在课本和试卷中,而是也和自己的日常生活紧密联系,如此方能唤醒学生自身了解和掌握知识的欲望.[2]在设计该教学环节时,引导学生从生活中寻找轴对称图形,鼓励学生发散思维、大胆列举,帮助完善、给予肯定,给学生获得成功的体验,唤起学生掌握知识的兴趣.
在教学时,将课堂的主动权交给学生,让学生自主探索、合作交流.给学生足够的时间来经历观察、思考、操作、实践这一数学学习过程,通过自己动手剪轴对称图形,巩固对轴对称图形的概念认知和灵活运用;通过画轴对称图形的对称轴,规范对称轴的画法……
结合智慧课堂,可高效率地收集学生的反馈信息并及时点评和指导,在有限的课堂时间内,最大化地丰富课堂内容.
1.5 实践应用之摆一摆
教师:现在有5 个全等的正方形组成的图形,只移动其中的一张纸片,不重叠的摆放,你能使它变成轴对称图形吗?在自己的平板端尝试操作,尽可能多地找出不重复的情况.
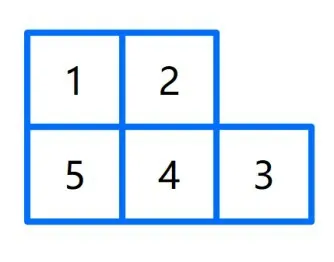
学生踊跃展示:

教师:这个问题的结果有很多种,我们在探究一个问题时,不要盲目地试,而是要根据题目所给的条件,有条理地思考.题目说只移动一张纸片,我们在探究时,可以怎么思考?
学生19:只移动一张纸片,我们可以分5 种情况讨论.
教师:比如说我们移动3 号纸片,其余的四张纸片不动,你发现了什么?
学生19:其余四张纸片构成一个正方形,是轴对称图形.
教师:在轴对称图形的基础上,我们再添加一个正方形,使得新组成的图形仍然是轴对称图形,可以怎么添加?
学生20:可以在它的对称轴上安放3号正方形.
教师:(展示课件)以此类推,移动其他的正方形纸片呢?如果保持不动的四张正方形纸片,不是轴对称图形呢?大家可以课下自己好好探究一番.
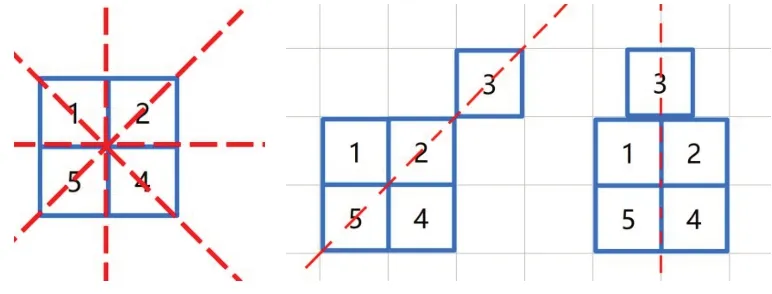
教学说明:
在认识了轴对称图形、会剪简单的轴对称图形以及能画轴对称图形的对称轴之后,笔者在这里设置了一道思维拓展题,利用智慧课堂让学生通过学生平板自主探究,设置无限克隆模式,使得学生能够无限次的反复移动正方形纸片来操作验证;将图形置于网格纸中,使得学生借助于网格纸能够很好地判断所得图形是否为轴对称图形,在直观感知的基础上,体会数学的严谨性.
活动探究课往往是热闹的、互动性极强的,在热热闹闹的课堂活动背后,也想更深层次的教会学生思考问题的方式,而绝非盲目的操作.
1.6 课堂小结
再回首:本节课的课程内容已经结束,我们一起回顾一下今天整个学习过程.
齐展望:其实轴对称图形是大有用处的,在往后的学习中,我们会在二次函数、菱形、圆的学习中再次见到它大展身手,希望各位同学能够在轴对称图形这一部分打好基础,为后续的学习做好准备!
教学说明:
在课堂小结中,带领学生回顾整个学习过程,帮助学生梳理本节课所经历的观察、猜想、操作、实践等一系列思维活动,更深一步地建立思考问题的方式方法;带领学生展望未来,为后续学习埋下种子.
1.7 课后实践与作业
(1)查阅渡江战役纪念馆相关资料,了解革命先辈的英勇事迹;
(2)完成双喜图的裁剪制作(选做);
(3)找规律:在横线的空白处填上恰当的图形.

教学说明:
减轻学生作业负担迫在眉睫,就要求教师摒弃大量目标盲目、繁杂重复的作业,面向全体学生设计和布置高质量的作业,既能让后进生在其能力范围内能得到练习巩固、又要让优等生得到思维的锻炼和提升.
本节课精心设计了三项作业:第一项结合课堂引入的渡江战役纪念馆,提倡学生拓展自己的知识面,通过查阅资料了解革命史实;第二项是裁剪制作双喜图,该项有一定的难度,旨在考查学生对于轴对称图形的概念是否掌握以及能否灵活运用,设为选做,供基础较好的学生来思考锻炼;第三项是一道规律探究题,旨在锻炼学生的观察、分析能力.三项作业既能巩固课堂所学,也灵活有趣,能够满足不同层次的学生.
2 几点思考
2.1 提高课堂教学质量,智慧课堂提升教学智慧
“双减”政策之下,学生再也不能通过大量的题海战术和课外培训班的辅导,来提升自身的能力水平,教育的重心回归校园,更是回归课堂.教师能否在有限的课堂时间,高效率地完成课堂教学,将是学生能否成长进步的关键.
高效的课堂教学,应该达成这样两个目标:(1)在明确教学目标的情况下,把握教学的重点和难点,达到知识育人的目的;(2)在实际教学过程中,教师要关注到每一位学生,既要对优等生进行提升培养,也要对后进生给予帮助指导.前者,需要教师更新教育观念,认真推敲每一个教学环节,摒弃照本宣科的做法,在丰富课堂环节的同时,既要使得学生掌握必备的知识,也要教会学生思考问题的方式、引导其构建积极的情感、态度、价值观;后者,要想在有限的课堂教学中关注到每一位学生,传统的课堂是很难兼顾的.智慧课堂之下,信息化手段能够帮助教师得到每一位学生的学习反馈,当堂发现问题并有针对性的给予指导,使得教师真正实现因材施教.
2.2 提升作业布置质量,智慧思考打造智慧学生
一直以来,教师对于家庭作业的布置都是“一网打尽”:不管学生的程度差异,统一做同一份资料的所有习题.所谓的“题海战术”,其原理就是大量的重复训练可以帮助学生强化对于知识的理解和运用,反复的刷题能够帮助学生掌握答题技巧,从而实现成绩的提升.然而“题海战术”往往消耗大量的时间而得到少量的进步,效率不高,大量重复刷题在加重学生负担的同时,反而消耗其对于学习的爱好和兴趣,久而久之把学生塑造成“少有思考、机械刷题”的工具人.
教师要探究、设计高质量的作业,有针对性地面向学生布置,使得学生能够花适量的时间而得到针对性的提升.【3】
对于学生完成的作业,教师要做到全批全改,在智慧课堂之下,教师可以针对每一位学生,汇总记录其作业完成情况、薄弱点分析,建立其专属学习档案,追踪其一段时间内的课堂学习和作业反馈,及时了解每一位学生的学习动向,及时进行针对性的调整.

