用问题驱动数学建模素养落地

徐黄

[摘  要] 数学建模与解题能力的培养本身并非一对矛盾的事物，同时重视数学建模素养的培养，能够为学生的可持续发展奠定基础. 将数学方法进行整合，将问题情境与数学知识进行联系，寻找恰当的数学方法来解决相关的问题，最终形成一个指向问题解决的数学模型. 很显然，在这样的逻辑当中，解决问题是学生运用数学模型的潜在动力，因此为学生创设问题情境，就可以给学生创造一个很大的数学建模的空间，从而实现数学学科核心素养中数学建模素养的培养.

[关键词] 高中数学;数学建模;数学问题

在《普通高中数学课程标准（2017年版）》中，关于数学学科核心素养以及数学建模的相关阐述是这样的：数学核心素养是数学课程目标的集中体现，是在数学学习的过程中逐步形成的. 高中阶段数学核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数学分析. 这些数学核心素养既有独立性，又相互交融，形成一个有机整体. 将这段阐述与高中数学教学的传统联系起来进行理解，可以发现实际教学当中存在着理论与实践的矛盾. 化解这样的矛盾，需要教师对理论进行深度学习，对实践进行深度反思，对理论与实践的关系进行深度探究. 由于数学学科核心素养包括六个要素，在此不可能一一阐述，仅以其中的数学建模素养为例进行论证.

从理论的角度来看，数学建模的重要性，可以说每个数学教师都高度重视，即使是对数学建模概念不熟悉的教师，当遇到学生解题能力比较薄弱时，也会归因为“学生建立模型的能力比较差”. 事实上，随着素质教育的不断普及，高中数学建模教学受到了人们的广泛关注. 但是这种关注具体在教学实践的过程中，似乎又没有真正转化为数学建模的教学过程，当下的许多高中数学课堂上，教师所走的依然是知识讲解加习题训练这样一条老路. 尽管由于高考评价的需要，教师不得不将相当一部分精力投入到学生的解题训练中，但是数学建模与解题能力的培养本身并非一对矛盾的事物，同时重视数学建模素养的培养，能够为学生的可持续发展奠定基础. 因此加强数学建模的教学，对于学生而言可以说是一举两得的事情，在核心素养培育的背景下应当予以高度重视. 那么在当前的高中数学教学中，如何实现数学建模素养的培养呢？事实证明，创设问题情境在高中数学教学中得到了广泛应用，以创设问题情境驱动数学建模教學，可以成为一种非常有效的教学方法.

[⇩] 高中数学教学中问题驱动数学建模的可能性的探究

利用问题驱动数学建模是否可行，这一探究值得重视，教师必须做出一定的理论探索. 众所周知，数学建模是联系数学知识与实际应用的重要桥梁，是数学知识走向实际应用的必然途径. 要让学生体会到数学知识的这种应用性，就必须引导学生去思考数学知识何以能够得到普遍应用. 而要想让数学知识在数学领域乃至于生活领域中得到广泛应用，很重要的一点就是要帮助学生建立数学模型. 那么数学模型的建立与问题驱动又存在什么样的联系呢？从逻辑的角度来看，数学知识的实际应用往往是由问题来驱动的，也就是说当学生在生活中或者数学学习中遇到问题时，学生的第一反应往往是如何去解决这些问题. 而在解决问题时常常会涉及数学因素——这实际上是非常普遍的，包括很多生活问题的解决，即使没有直接运用到数学知识，也会运用到数学思维. 根据著名数学教育专家史宁中教授的观点，这种情况下就需要学生能够运用数学的眼光看事物、思考问题，这就是数学核心素养的体现，与数学建模有着密切的关系.

这也就是说，如果在数学教学的过程中，能够引导学生去深度思考如何解决一个问题，那么学生就会思考如何运用所学到的数学知识. 运用数学知识的过程显然不是一个拿来直接套用的过程，而是这样的一个过程：将数学方法进行整合，将问题情境与数学知识进行联系，寻找恰当的数学知识来解决相关的问题，最终形成一个指向问题解决的数学模型. 很显然，在这样的逻辑当中，解决问题是学生运用数学模型的潜在动力，因此为学生创设问题情境，就可以给学生创造一个很大的数学建模的空间，从而实现数学学科核心素养中数学建模素养的培养.

[⇩] 在教学实践中用问题驱动数学建模素养落地

在数学学科核心素养的组成要素当中，数学建模素养起着承上启下的作用. 虽然说数学学科核心素养要从六个方面来阐述，但实际上数学抽象与逻辑推理都是数学建模的基础，一个数学模型建立起来后，不可避免地会运用到数学运算、数据分析等. 因此培育学生数学学科核心素养时，抓住数学建模这一素养进行培养，可以对其他核心素养要素的培养起到牵一发而动全身的作用. 基于用问题驱动数学建模素养落地的思路，基于数学建模与数学探究活动完整的教学设计，一要创设真实的问题情境，强化情感驱动;二要渗透“实践与创新”理念，培养学生的高阶思维;三要加强学科内外的知识整合，突出思辨思维;四要注重信息技术与数学课程的深度融合，提高教学的实效性. 下面以人教版“立体几何”的教学为例进行说明.

立体几何的研究对象是立体图形，所运用的语言是数量关系. 对于高中数学而言，立体几何的研究对象大多来自生活，都是从生活中抽象出来的. 不少高中学生由于空间想象能力薄弱，在解决立体几何相关问题时，常常是捉襟见肘. 这时如果能够帮助学生建立起利用数学模型解决问题的意识和能力，那么就可以让立体几何知识的教学起到事半功倍的效果. 这样的一个数学建模过程，自然也就应该在问题情境中去完成.

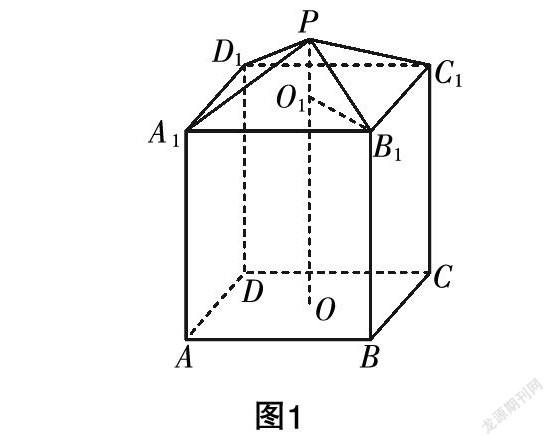
比如几何知识初步学习完毕后，笔者给学生提出了这样一个问题：“某公司需要设计一个仓库，其由上下两个部分组成：上部分是一个正四棱锥P-ABCD，下部分是一个正四棱柱ABCD-ABCD（如图1所示）. 设计要求正四棱柱的高是正四棱锥高的4倍. 问：如果正四棱锥的侧棱长是6米，那么当PO的值是多少时，仓库的容积最大？”

这个问题完全可以视为从生活中抽象出来的，在解决这个问题的过程中，可以帮助学生培养数学建模的意识和能力. 由于该问题要求的是仓库容积的最大值，也就意味着摆在学生面前的是一个动态变化量，这是绝大多数学生感觉到有挑战性的问题类型之一. 解决这类问题很多时候是借助于函数关系来完成的，而函数关系的建立，本质上就是数学模型的建构——在实际教学中要帮助学生明确这一思路. 具体到这个问题的解决过程中，让学生在问题情境里尝试自主寻找函数关系式. 很显然，要求的是仓库容积的最大值，根据题意发现这个最大值与PO有关，因此只要找到这个关系，问题就能迎刃而解了. 这样一个认识的形成过程，本质上就是一个数学建模的过程，当学生最终得到解析式V=V+V=12h（36-h2）（0<h<6）时，实际上就完成了一个数学模型的建立.

[⇩] 问题驱动数学建模素养落地是数学教学的新方向

在上面的这个例子当中，数学模型的建立过程是在问题情境当中完成的，在问题的驱动下，学生面对着具体的问题情境，通过对立体图形的分析，然后想到用函数知识去解决问题，并且通过逻辑推理建立起了函数解析式，于是问题迎刃而解. 很显然，在这样的一个问题情境中，通过问题解决，学生经历了一个比较完整的数学建模的过程，这也就打下了数学建模素养落地的基础.

尤其值得强调的是，在这样的一个过程中，为了强化数学建模素养落地，教师有必要在学生解决问题的过程中，将数学建模的过程以一定的形式传递给学生. 比如，寻找仓库容积与正四棱锥高的关系，不只是一个寻找数学关系的过程，也是一个建立数学模型的过程;再比如，教师还可以基于这一问题的解决，向其他问题延伸，让学生经历一个演绎的思维过程，从而认识到寻找数学关系常常是许多问题得以解决的关键. 而寻找与建立数学关系，本质上就是建立数学模型. 在数学教学的过程中，创设问题情境、进行问题解决是高频率的事情，因此只要将这样的认识不断地重复，久而久之，学生就能够形成数学建模的意识，并且会主导自身培养数学建模能力.

总而言之，在核心素养培育的背景下，问题驱动教学走进了高中数学课堂. 实践证明，问题驱动教学对培养学生的学习兴趣和提高学生的创新思维能力具有促进作用，对数学建模能力的培养也有着重要的作用，数学教学中必须高度重视.