PME视角下的“函数的零点”概念教学设计

⦿西华师范大学 王 雪 李中平

1 研究背景及问题的提出

1.1 研究背景

数学概念是构成数学知识的基础，是基础知识和基本技能的核心与灵魂.理解概念是一切数学活动的出发点.如果教师过分偏重解题技巧而忽视概念的教学，那么会导致解题时学生只知解题套路却不懂原理.“数学教育心理学(psychology of mathematics education，简记为PME)是研究学生学习数学的心理规律以及教师如何根据学生学习数学的心理规律进行有效教学设计的学科”[1].PME理论对学生的学与老师的教都有很强的指导意义，在进行概念教学时从PME视角透视教学内容，设计出符合学生学习心理规律的教学设计.

1.2 问题的提出

著名数学家高斯曾经指出:“在数学中重要的不是符号，而是概念.”[2]数学概念教学一直都是教学重点，然而学生仍然会混淆某些数学概念.“函数的零点”是函数的进一步应用；函数的零点概念作为函数概念的延伸，学习函数的零点概念也可加深对函数概念认识和理解；但函数的零点也是易混淆的概念，如果不能合理地融入到已有的认知结构中，那么就很难从大脑中提取出来进行灵活运用.

“其实概念的形成与转变是一个连续动态的心理历程”[3].因此在“函数的零点”概念教学时，考虑从PME视角透视教学，在学生学习函数零点概念的心理活动基础上，去把握知识的传授过程，帮助学生建立良好的认知结构.函数的零点概念教学的关键在于结合学生学习函数的零点概念的心理活动和学生现有的认知发展水平，引领学生对概念探究、理解，经历概念的形成过程，准确把握住函数零点的外延与内涵，多元化表征概念，同时能运用到具体情境中.

那么教师如何从PME视角实施函数的零点概念教学？学生如何明晰概念的外延和内涵？是否能多种形式表征函数的零点概念？

2 理论基础

2.1 现代认知心理学下的知识

现代认知心理学根据知识的不同状态和表述形式将知识广义地划分为陈述性知识和程序性知识，其中陈述性知识是指“是什么”，程序性知识则是指“怎么做”.数学概念是人们对客观现实世界中的数量关系和空间形式本质属性的思考在头脑中的映射.因此数学概念属于较为复杂的陈述性知识，概念的应用对应的技能则属于程序性知识.当数学概念被学习者“隐性”获得纳入知识结构后，在应用数学概念时会转换成相应技能“显性”表现成概念的形成情况.

2.2 数学概念特征下的多元表征

从概念学习的心理角度来说，数学概念的表征具有多元性特征.若学生没有理解概念就不能用另一种表征方式去表达概念，所以在教学过程中必须注重概念形式的转换.2000年美国NCTM在《学校数学课程标准与原则》中指出的“不同的表征将导致不同的思维方式”，意味着在多角度理解概念的同时也在发展学生的逻辑思维.

2.3 概念同化

概念的学习有概念形成、概念同化两种方式.而高中阶段的学生对函数已经具备了一定的认知，因此从PME视角下选择概念同化是最好的教学方式.概念同化即利用已掌握的概念去学习新概念，主动与认知结构中原有的相关概念相互作用，由此获得新概念的过程.概念同化的心理过程包括辨别、同化、强化.

2.4 信息加工学习理论下的学习过程

加涅(R.Gagne)认为学习的过程就是一个信息加工的过程.信息加工学习理论将学习活动及主要的心理活动进一步拆分，把学习过程划分为八个阶段，且各自发挥不同的功能.第一阶段是“动机”，激发学习动机，产生学习期望.第二阶段是“了解”，把注意力集中在与学习目标有关的刺激上.第三阶段是“获得”，学生对新获得的刺激进行编码、贮存.第四、五、六阶段分别是“保持”“回忆”“概括”，将获得的信息都贮存在长时记忆中.“保持”阶段注意信息的贮存，避免新旧刺激的干扰.“回忆”阶段，把信息合理地从大脑中提取.“概括”阶段，将学习的知识迁移到不同情境中.第七阶段是“操作”，通过作业反映出学生的学习效果.第八阶段是“反馈”，在强化的同时促进信息的有效加工.

基于PME视角研究的需要，综合数学概念表征的多元性、概念同化的心理过程与信息加工学习理论下的学习过程，因此将函数的零点概念教学过程概括为四个环节：概念探究、概念表征、概念同化、概念应用.

3 函数的零点概念教学过程

3.1 概念探究——激发动机引起注意以揭示本质属性

教师：大家回忆从初中到现在都学习了哪些函数？又学到了函数的哪些知识呢？

学生1：一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数，学了图象和性质.

教师：那同学们能不能画出一次函数y=2x+1的图象，接着观察函数图象与x轴、y轴相交的点.我们把图象与x轴交点的横坐标称为函数的零点，在这个图象(如图1)中与x轴交点的横坐标-0.5称为一次函数y=2x+1的零点，那么思考一下零点的本质是点还是数？如果是数，是有理数还是实数？

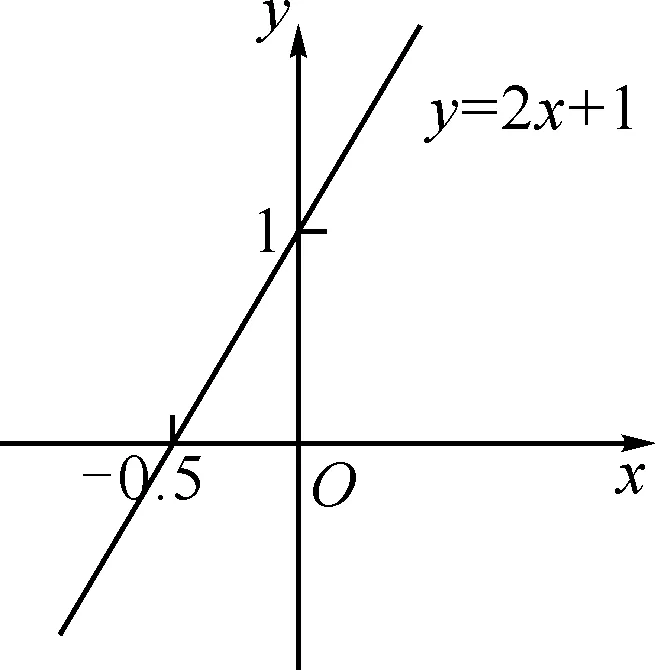
图1

学生2：是实数.

教师：很好，那么是不是只有一次函数有零点呢？接着试着描点画出二次函数y=x2-2x-3的图象，与x轴交点的横坐标是多少？那么该函数的零点是多少？有几个零点？

学生3：函数图象(如图2)与x轴交点的横坐标是-1,3，因为函数与x轴交点的横坐标是函数的零点，所以该函数的零点是-1,3，有两个零点.

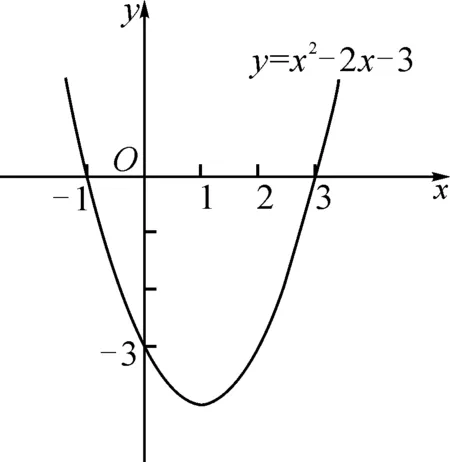
图2

设计意图：回顾简单旧知，激发学生的学习兴趣，使之产生学习动机.引导学生从函数图象上感受零点的存在，计算函数的零点并且得出零点的本质是实数.层层诱导，逐步唤起旧知的同时还可以增强学生学习数学的信心.

3.2 概念表征——获得概念保持记忆以转换多种形式

教师：根据上面我们画出的函数图象中有零点的存在，思考所有的函数都有零点吗？请举例.

学生4：不一定，因为函数与x轴交点的横坐标是函数的零点，如果所给函数与x轴无交点，那么该函数就无零点，比如反比例函数.

教师：在画函数y=2x+1，y=x2-2x-3图象时，如何求函数图象与x轴交点的横坐标？

学生5：使2x+1=0，x2-2x-3=0，算出x，就是函数图象与x轴交点的横坐标.

教师：对，很不错.对于一般函数y=f(x)，试着类比得出函数零点的概念.

学生6：对于函数y=f(x)，使f(x)=0的实数x就叫做函数y=f(x)的零点.

教师：非常好，这就是函数零点的概念.接着思考x2-2x-3=0，2x+1=0是方程还是函数？零点是方程的零点还是函数的零点？两者之间有什么关系，结合图象来看呢？

北运河流域全境共划分为346条小流域，其中山区37条，平原286条，山区—平原21条。按照北京市水土保持类型区划分，北运河流域地跨北京市全部4个类型区，其中城市径流控制区 2 434km2，含224个小流域；地下水源涵养区757km2，含72个小流域；地表水源涵养区735km2，含34个小流域；土壤侵蚀控制区320km2，含 16 个小流域（见图1）。

学生7：2x+1=0，x2-2x-3=0是方程，零点是函数的零点，函数所对应的方程f(x)=0的实数根就是函数的零点，也即函数y=f(x)的图象与x轴交点的横坐标.

教师：试着先算出y=2x+3的零点，再在x轴上表示出零点.

设计意图：根据图象及零点的存在位置，逐步追问得到零点的外延与内涵：外延——图象与x轴交点的横坐标，内涵——对于函数y=f(x)，使f(x)=0的实数x.诱导学生得出零点的概念，使其明晰外延和内涵.学生7的回答切实体现出学生对函数零点与方程根之间的关系的理解，从数、形上表示零点，转换不同形式进行多种表征以促进思维的发展.

3.3 概念同化——提取概念情境概括以促进知识理解

教师：根据前面可得出y=x2-2x-3有零点，y=x2-2x-3是二次函数，回忆并动手画图象，思考二次函数y=ax2+bx+c(a≠0)都有零点吗？有几个零点？请给出理由.

学生8：二次函数y=ax2+bx+c不是都有零点，有零点的话，就使ax2+bx+c=0，算出方程的实数根，方程实数根的个数就是函数零点的个数.那么就考虑ax2+bx+c=0中x的情况.

教师：那么回到了ax2+bx+c=0中求实数根的情况？会用到什么？

学生9：对，会用到判别式.

表1

注：a≠0.

教师：当函数y=f(x)=g(x)-h(x)时，如何求函数f(x)的零点？提示：从零点的概念出发.

学生10：要求函数的零点就是使f(x)=0，即g(x)-h(x)=0,即g(x)=h(x)，就是求使等式成立的实数x.

教师：很不错，回到y=x2-2x-3，根据式子的转换，用画图象的方式求函数的零点.

学生11：首先y=x2-2x-3转换成y=x2-(2x+3)，其中把x2看作是g(x)，把2x+3看作是h(x)，那么就是求使x2=2x+3成立的x.分别画出y=x2，y=2x+3的图象，会发现有两个交点.

教师：这两个交点与之前所求出来的零点有相同点吗？说出尽可能多的发现.

学生12：交点的横坐标就是零点的值，交点的个数是零点的个数.

设计意图：通过二次函数判别式，得出二次函数不同情境下零点存在情况.表格让学生直观感受到二次函数中方程的根、图象与x轴的交点、函数的零点之间的联系，让学生主动接纳知识，加深对零点的理解.考虑y=f(x)=g(x)-h(x)的情况，给予学生思路去探究，鼓励学生发现求函数的零点是求两个函数的交点的横坐标，拓宽学生思维.

3.4 概念应用——操作作业强化概念，实现知识迁移

教师：总结函数的零点概念，完成下面的练习题：

(1)求一次函数y=kx+b(k≠0)的零点；

(2)y=x2-2x-1是否有零点？

(3)y=x3+2x+1有几个零点？

(4)y=lnx+2x-6是否有零点？

学生可以根据以上所学完成习题：通过求方程的实数根、函数图象与x轴交点的横坐标、拆分为两个函数的交点，去判断零点的值、零点是否存在及零点的个数.

教师：思考函数的零点、方程的根、与x轴交点的横坐标、两个函数的交点之间的关系？

学生13：函数y=f(x)的零点对应方程f(x)=0的实数根，也是与x轴交点的横坐标，实数根的个数=交点数=零点个数；对于y=f(x)=g(x)-h(x)函数形式，两个函数交点的横坐标就是y=f(x)的零点，交点数=零点个数.

设计意图：通过零点概念的应用可以反馈出学生对零点概念的掌握情况.引导学生从数到形，从形到数，从方程到函数图象，从函数图象到方程把握零点的外延和内涵，进一步强化函数零点的概念，自然纳入认知系统中进行信息加工处理.

4 结论与建议

4.1 PME视角下的“函数的零点”概念教学的必要性

中学阶段是学生生理、心理和智力发展较快的时期.这一时期的学生受心理特征和能力基础的约束，刚进入高一的学生在面临难度更大、更抽象的数学知识以及初高中教师不同的教学方法时，会遇到一定的学习“障碍”.数学教师的首要教学任务就是扫除这种“障碍”.函数本身就作为抽象的存在，函数的零点概念是教学的重点.从PME视角审视概念教学，打破学生的思维定式，发展其抽象思维.以学生可接受的教学方式把函数的零点概念进行信息加工，同化到知识结构中，促进良好知识结构的形成.

4.2 对函数的零点概念教学的建议

在实际的中学数学教学中，教师总把更多关注点放在学生的解题能力上，“而忽视数学概念在心理层面的发展与形成，极容易造成学生对于概念的理解只是停留在机械的记忆层面”[4].对“函数的零点”教学时要把握学生心理，进行层次训练促进思维逐步发展，同时渗透数学思想、数学方法并与后面的知识建立联系；从形的角度理解零点的概念，从数的角度给出解答时要具有严密的逻辑性；课堂结尾引导学生总结得出零点的不同表征方式，切实把握概念的内涵与外延.