“1”在数学解题中的妙用初探

⦿甘肃省天水市第九中学 陶建宏

1 引言

在解答数学题目时，经常会碰到一些觉得束手无策的情况，但通过仔细思考，不难发现题目中隐含的一个数“1”，若能发现这个数，将会收到意想不到的效果，下面通过几个题目加以说明.

2 “1”的妙用

2.1 “1”在求三角函数值问题中的运用

例1已知tana=2求4sin2a-sinacosa-cos2a的值.

分析：这个题目如果由tana=2出发去求sina和cosa的值，再代入所求式子方可求出，但是在求sina和cosa的值时要分第一和第三象限两种情况进行讨论，并且在第一和第三象限sina和cosa的正负相同，在两种情况下得到的答案相同，但作为一个解答题时必须分两种情况进行计算.可是如果我们再好好观察不难发现所求式子的分母是经常容易被人们忽视的“1”，而这里1=sin2a+cos2a再将分子分母分别除以cos2a，从而化为了正切的形式.

详解：4sin2a-sinacosa-cos2a

注意：这里分母是“1”很少能引起人们的注意，以为没有分母，而实质分母是容易被人们忽视的“1”.在三角函数部分多用1=sin2a+cos2a.

再比如，2007年全国高中数学联赛河南省预赛(高二)中有这样一道题目：已知7sinα+24cosα=25，则tanα=( ).

分析：对于此题如果能求出sina和 cosa的值，再利用商数关系可以求出tana的值，但是这很难求解.若对原式两边平方，再注意到sin2a+cos2a=1，得

(7sinα+24cosα)2=252×1=252[(sin2a+cos2a]，展开整理得(24sinα-7cosα)2=0.

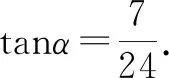
通过这两个题目让学生在三角函数化简求值中注意这个很重要的数字“1”以及1=sin2a+cos2a.

2.2 “1”在指数、对数中的运用

在数学解题中，若能根据题目特征巧妙地利用“1”作代换，常能出奇制胜，取得较好解题效果.比如在指数和对数中经常会遇到一些有关“1”的问题.

例2解方程4x-2=1.

解析：因为a0=1(a≠0)，所以4x-2=40，得x-2=0，即x=2.

看起来这是一个简单的指数方程问题，但如果不知道a0=1(a≠0)这个条件，就无法更简单求解.

例3解不等式lgx>1.

解析：因为logaa=1(a>0且a≠1) 所以lg10=1.又根据对数函数的单调性，由lgx>lg10，得x>10.

例4函数y=loga(x-4)的图象恒过定点________.

解析：因为对数函数y=logax(a>0且a≠1)的图象恒过点(1,0),由x-4=1,可得x=5.则函数y=loga(x-3)的图象恒过定点(5,0).

指数函数与对数函数恒过定点是考试常考的一个知识点，它都涉及常数“1”.

通过这几个题目可以看出在指数与对数中“1”显得特别重要.要注意“1”这个特殊的数字，它的作用非常大，不能藐视.

2.3 “1”在求多元函数最值问题中的运用

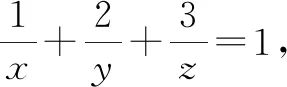
分析：这个题目是求多元函数最值的一个常见题目，学生刚开始觉得不好做，但若能灵活运用已知条件中的“1”作适当的整体代换，再利用均值不等式方可求解.

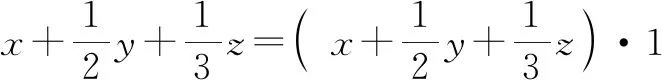
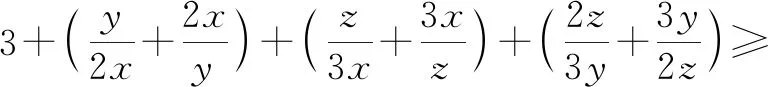
3+2+2+2=9，

当且仅当x=3,y=6,z=9时取得最小值9.

此题如果不能注意到“1”乘任意一个数都得这个数的话，这个题目就无法更简单求解.

2.4 “1”在求多元条件下代数式的最值问题的运用

例6已知x>0,y>0且x3+y3=2，试求x+y的最大值.

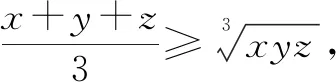
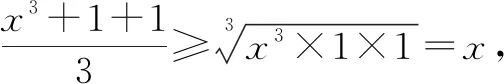
所以x+y的最大值是2，当且仅当x=y=1时取到最大值2.

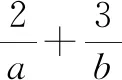
2.5 “1”在求无理式的最值问题中的运用

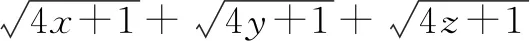
分析：解决这个题的关键是如何去掉根号，这样才能利用x+y+z=1这个条件.在选修教材4-5中，学习了柯西不等式求最值，这个题就可以利用柯西不等式去求解.

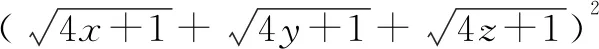
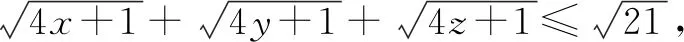
3 结束语

通过以上五类问题的典型例题，在求代数式的值或最值时，如果注意到“1”这个特殊数字，巧妙地利用“1”作代换，往往可以帮助我们把一个复杂的题目简单化，从而达到事半功倍的解题效果.这里仅列举了有针对性的七道例题，以达到抛砖引玉的目的.而实质上“1”这个简单数字还有好多作用，这需要我们在平时的教学实践中，做一个教与学的有心人，审题时要注意挖掘隐含条件，解题过程中要多做一些反思与总结，通过总结去加深理解并学以致用，从而提高解题能力、发散思维能力和探究归纳的能力.