围绕生活命制试题 渗透文化提升素养
⦿上海市奉贤区景秀高级中学 沈 健
1 问题提出
数学发展到今天,显现出一个突出特点:数学与人类生活和社会发展发生着越来越紧密的关联.“数学与人类生活和社会发展紧密关联.数学不仅是运算和推理的工具,还是表达和交流的语言.数学承载着思想和文化,是人类文明的重要组成部分.”[1]《普通高中数学课程标准(2017 年版)》中的这段表述从多个维度揭示了现代数学与人类生活和社会发展的关系,也多样化地展现出现代数学所具有的价值和功能.
那么,如何围绕生活命制试题,同时达到渗透数学文化提升数学核心素养的目标呢?各地试题又是如何考查的?本文中选取典型试题加以举例,以期抛砖引玉.
2 实例剖析
2.1 以音乐为背景
例1(2020秋·潍坊期末)音乐,是人类精神通过无意识计算而获得的愉悦享受.1807年法国数学家傅里叶发现代表任何周期性声音的公式是形如y=Asinωx的简单正弦型函数之和,而且这些正弦型函数的频率都是其中一个最小频率的整数倍,比如用小提琴演奏的某音叉的声音图象是由图1,2,3三个函数图象组成的,则小提琴演奏的该音叉的声音函数可以为f(t)=( ).
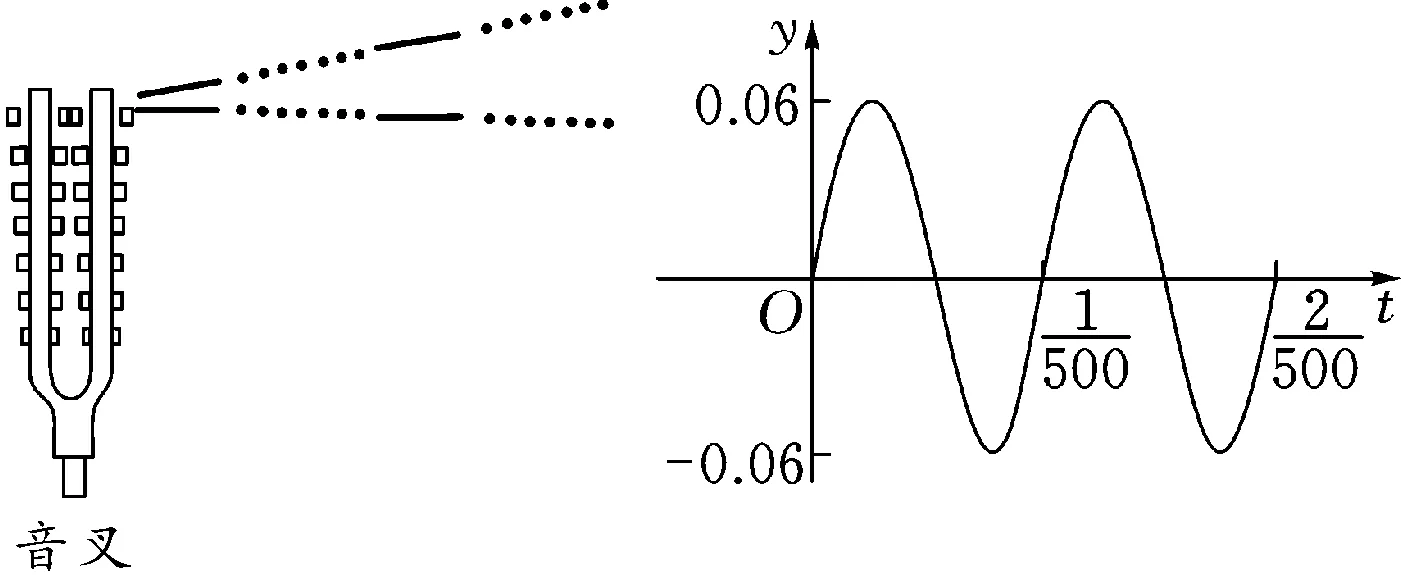
图1
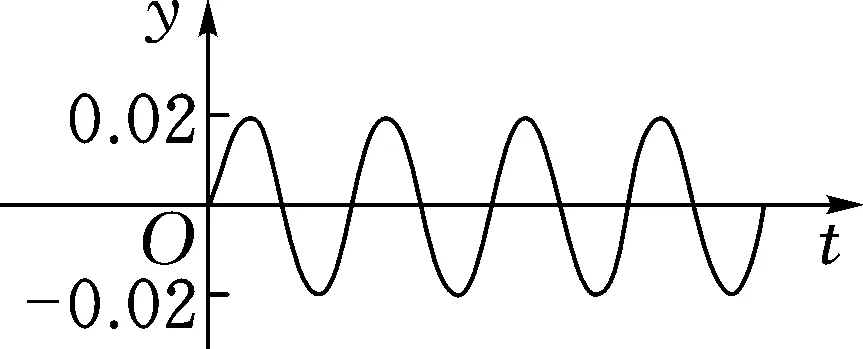
图2
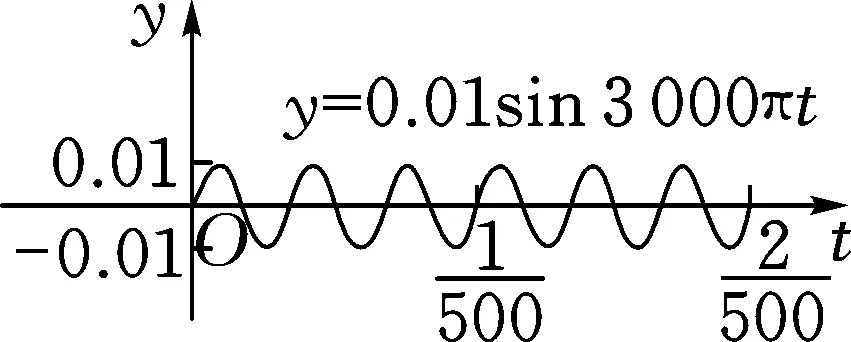
图3
A.0.06sin 1 000πt+0.02sin 1 500πt+0.01sin 3 000πt
B.0.06sin 500πt+0.02sin 2 000πt+0.01sin 3 000πt
C.0.06sin 1 000πt+0.02sin 2 000πt+0.01sin 3 000πt
D.0.06sin 1 000πt+0.02sin 2 500πt+0.01sin 3 000πt
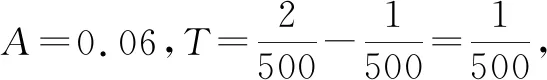
结合题意知,函数f(t)=0.06sin 1 000πt+0.02sin 2 000πt+0.01sin 3 000πt.
故选:C.
点评:本例以音乐为背景,考查利用图象求三角函数解析式的应用问题.由图1求出A,T,ω的值,写出对应函数的解析式,再结合选项得出函数f(t)的解析式.
本题考查学生阅读理解与解决实际问题的能力以及数学建模、数学运算、数据分析的核心素养,对立志学习音乐的学生的数学水平的提高大有帮助.
2.2 以美术为背景
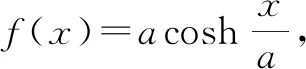

图4
A.cosh(x-y)=coshxcoshy-sinhxsinhy
B.y=sinhxcoshx是偶函数
C.(coshx)′=sinhx
D.若△PAB是以A为直角顶点的直角三角形,则实数m=0
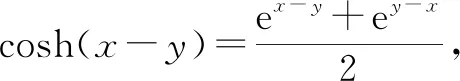
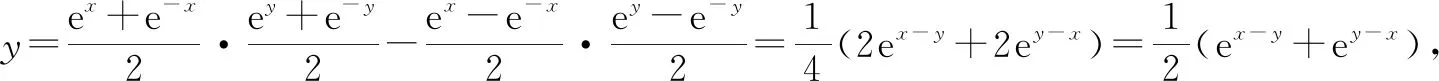
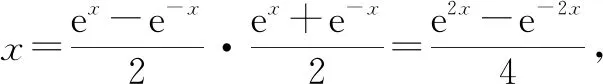
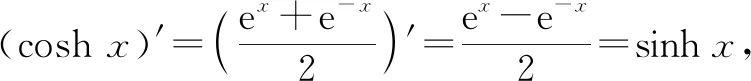
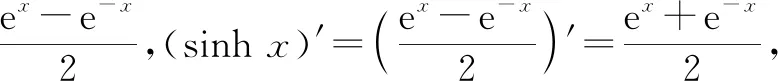
①
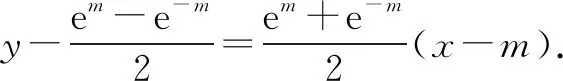
②
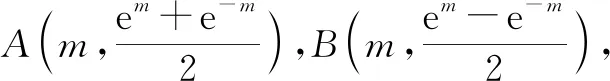
故选:ACD.
点评:本例以达·芬奇画作为情境引出著名的“悬链线问题”,命题者以自定义函数的形式,考查新定义函数的奇偶性和导数的几何意义,考查利用导数研究曲线上某点切线方程等基础知识、方程等基本思想和数学运算、逻辑推理、数学抽象的核心素养以及分析和解决问题的能力,对立志学习美术的学生的数学水平的提高大有帮助.
2.3 以体育运动为背景
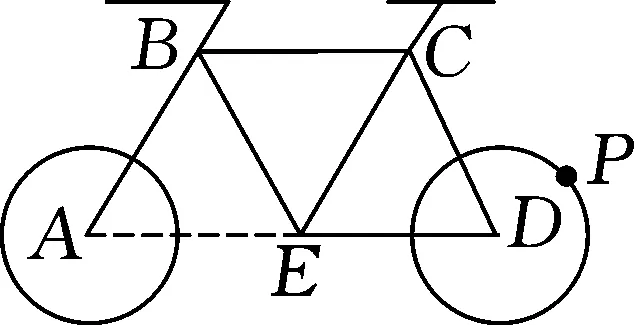
图5
A.18 B.24 C.36 D.48
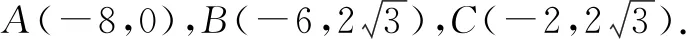
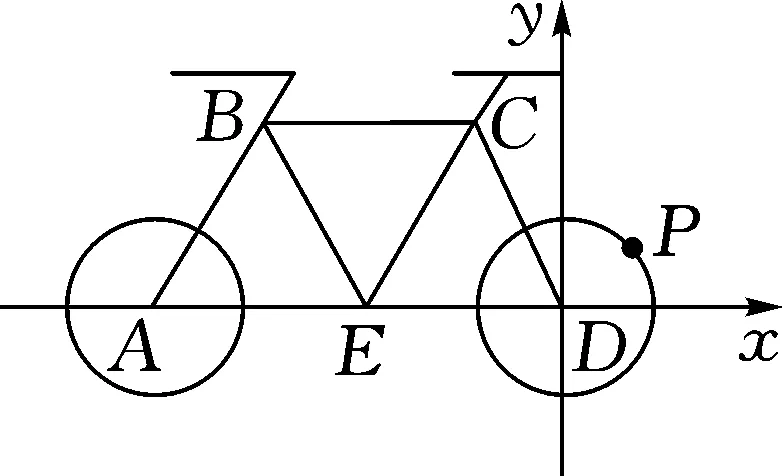
图6
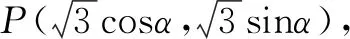

故选:C.
点评:本例从平常生活中某一自行车抽象出平面结构示意图,选取素材,考查数量积的运算、三角函数的性质在实际问题中的应用,同时考查了学生的数学建模的核心素养.根据题意建立平面直角坐标系,然后将涉及到的点的坐标求出来,其中P点坐标借助于三角函数值表示,则所求的结果即可转化为三角函数的最值问题求解,对立志学习体育的学生的应用数学能力水平提升大有好处.
2.4 以传统文化为背景
例4(2021·辽宁模拟)中国传统文化中很多内容体现了数学的“对称美”.如图7所示的太极图是由黑白两个鱼形纹组成的圆形图案,其特点是圆的周长和面积同时被平分,充分体现了相互转化、对称统一、和谐共存的特点.若函数y=f(x)的图象能够将圆的周长和面积同时平分,则称函数f(x)为这个圆的“和谐函数”.则下列命题中正确的有( ).

图7
A.对于任意一个圆,其“和谐函数”至多有2个
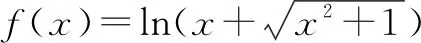
C.正弦函数y=sinx可以同时是无数个圆的“和谐函数”
D.函数f(x)=2x+1不是“和谐函数”
解析:因为过圆心的直线都可以将圆的面积及周长同时平分,所以对于任意一个圆,其“和谐函数”有无数个,故选项A错误;
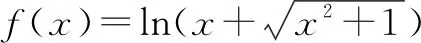
将圆的圆心放在正弦函数y=sinx的对称中心处,则正弦函数y=sinx是该圆的和谐函数,故有无数个圆成立,故选项C正确;
将圆的圆心放在函数f(x)=2x+1的图象上,则有无数个圆成立,故函数f(x)=2x+1是和谐函数,故选项D错误,
故选:BC.
点评:本题考查了函数的实际应用,以及学生对新函数定义的理解能力.
从数学的角度看,太极图是中心对称图形,数学爱好者一定对此图形也偏爱颇多.本题就是由此编拟出的一道函数的性质及应用题,靓丽之处是在简洁基础上与数学文化有机结合.
2.5 以数学与生活的联系为背景
例5(2021·淮安模拟)某保鲜封闭装置由储物区与充氮区(内层是储物区用来放置新鲜易变质物品,充氮区是储物区外的全部空间,用来向储物区输送氮气从而实现保鲜功能).如图8所示,该装置外层上部分是半径为2的半球,下面大圆刚好与高度为3的圆锥的底面圆重合,内层是一个高度为4的倒置小圆锥,小圆锥底面平行于外层圆锥的底面,且小圆锥顶点与外层圆锥顶点重合,为了保存更多物品,充氮区空间最小可以为( ).
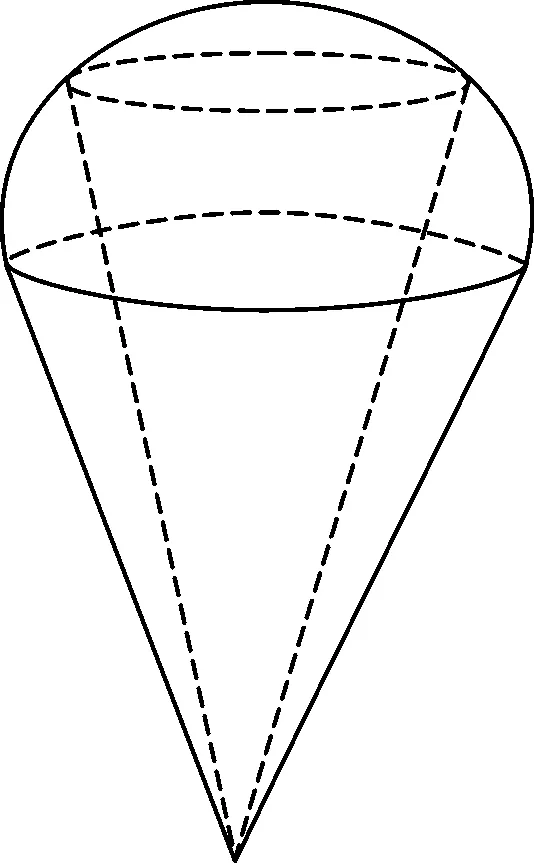
图8
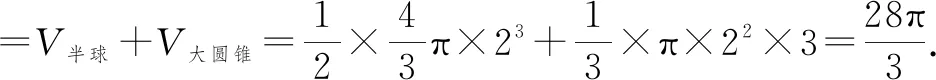
设小圆锥的半径为r,则
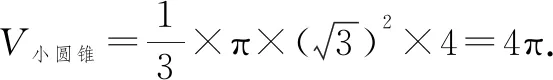
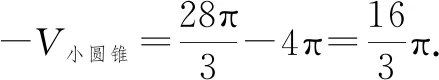
点评:本例以某保鲜封闭装置为背景,考查了圆锥的体积公式和球的体积公式,考查了逻辑推理、直观想象、数学运算的核心素养.充分展示了数学问题来源于生活并与生活紧密结合,并且贴近学生的实际,这样做有利于学生联系实际分析与解决问题,对于稳定学生在考试中的情绪和心态起到了较好的效果;探索了数学试题示意图的形式,使得数学抽象问题形象化.数学与生活息息相关.生活中有数学,生活也离不开数学.《普通高中数学课程标准》指出:“要重视从学生的生活实践和已有的知识中学习数学、理解数学.”数学是一门逻辑性很强的基础学科(概念、原理、法则),是比较抽象的.
3 结束语
基于新时代背景,基于创新人才的培养,我们要贯彻党的教育方针,坚持立德树人,倡导“五育”并举.

