应用GeoGebra开展数学探究活动的教学实践

⦿北京市第二十中学 张程艳

1 问题背景

《普通高中数学课程标准(2017年版2020年修订)》中指出，“数学探究活动是围绕某个具体的数学问题，开展自主探究、合作研究并最终解决问题的过程”，数学探究活动“不仅能够帮助学生更好地掌握知识技能，更能帮助学生学会数学的思考和实践，是学生形成和发展数学学科核心素养的有效载体”[1].在“互联网+”时代，信息技术成为学生进行数学探究活动的重要辅助手段，为学生的学习提供了丰富的资源.借助信息技术可以“更形象直观地显示概念的本质属性和特征”，“揭示数学变化规律，进行数学实验，猜想命题结论”，“探寻解决问题的途径”等等[2].可以说，信息技术的引入改变了学生的学习方式，使学生可以更主动、有效地进行数学学习.因此，教师要注重信息技术与数学课程的深度融合，开展数学探究活动，在落实“四基”“四能”的同时，发展学生的数学学科核心素养.

在众多数学软件中，GeoGebra作为集代数、几何、数据表和概率统计等功能于一体的动态数学软件，以其开源免费、功能强大、易于上手等优越性成为众多教师辅助教学的有力工具[3].应用GeoGebra开展数学探究活动，可以使抽象复杂的数学问题“可视化”，能够激发学生的学习兴趣和探究欲望，使学生在动手实践，亲身体验的过程中发展数学思维和创新能力.本研究以解析几何中的定点问题作为切入点，学生通过操作GeoGebra软件，在理解基本知识、掌握基本方法的基础上，充分经历发现问题、提出问题的过程，积累自主探索研究数学问题的经验，实现数学核心素养的进阶发展.

2 案例分析

2.1教学内容分析

在解析几何单元中，直线与圆锥曲线的位置关系是重点研究内容之一，对学生的转化与化归能力、逻辑推理能力、数学运算能力等都有较高要求，突出数学思想方法和数学核心素养的考查.其中，解析几何中的定点问题使学生在化“动”为“定”的过程中，体会“变”与“不变”的关联、“几何”与“代数”的完美融合，使学生在掌握基本解题策略的同时，挖掘问题背后呈现的规律，发展从数学角度发现问题、提出问题、分析问题及解决问题的能力.

2.2 学情分析

从学生的知识层面来看，在解析几何定点问题的第一课时中，学生通过对引例的分析，已经基本掌握了定点问题的解决策略.本节课将在此基础上设置数学探究活动，深入研究引例背后所蕴含的一般性规律.从学生的发展需求来看，学生更希望跳出解题的层面，探究问题的本质，在发现问题的基础上，自主提出问题，提升自身的实践创新能力.从学生的认知障碍来看，学生即使知道可以通过改变某一变量去研究定点位置的变化，也很难单纯通过纸笔运算发现运动变化背后呈现的规律.

因此，基于以上教学内容和学情的分析，本节课借助GeoGebra开展数学探究活动，大大降低探索过程的难度，使抽象的数学问题更加形象直观，让学生充分经历猜想、实验、探究、交流、反思的过程.

2.3 学习目标

(1)借助GeoGebra软件自主探究定点问题，透过现象看本质，尝试根据所发现的规律提出新的数学问题，提高从数学角度发现和提出问题的能力.

(2)在实验操作的过程中，体会从特殊到一般研究问题的方法，积累进行科学研究的经验；在自主探究、同伴互助的过程中，发展自主学习能力，提高实践创新能力，提升团队合作意识.

2.4 学习重点难点

重点：借助GeoGebra揭示解析几何定点问题背后蕴含的一般性规律.

难点：能够根据规律提出新的数学问题.

2.5 教学过程

环节一：问题初探，设计实验.

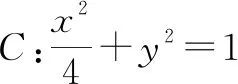
师：上节课同学们已经严格证明了直线MN过定点D(1,0)，请大家思考，引例中哪些要素的改变会对定点D的位置产生影响呢？

学生思考片刻，提出猜想，认为改变动点P所在的直线，或者改变椭圆的特征量a和b，或者改变点A,B在椭圆上的位置都会对点D的位置产生影响.

师：请同学们成立实验小组，设计实验方案，借助GeoGebra软件，尝试探索规律，并填写实验报告.

设计意图：学生在进行实验探究之前先分析成因，大胆猜想，明确实验方案，为后续进行自主探究做好合理规划，同时也能培养学生的数学直觉.

环节二：实验探究，发现问题.

在这个环节中，学生成立实验小组，分工协作，通过操作GeoGebra尝试发现问题背后蕴含的一般性规律，并作成果汇报.

(1)动点P所在的直线影响直线MN所过的定点.

通过在水平方向上拖动点P所在的直线(如图1，图2)，使直线与椭圆相离、相切、相交，学生发现点D的位置随着直线方程的改变而改变,但只要点P所在的直线方程确定，直线MN就恒过某一个定点.学生进一步探究点P所在直线方程x=t与定点D坐标之间的关系，通过记录实验数据，分析数据关系，得出如下的数学结论：

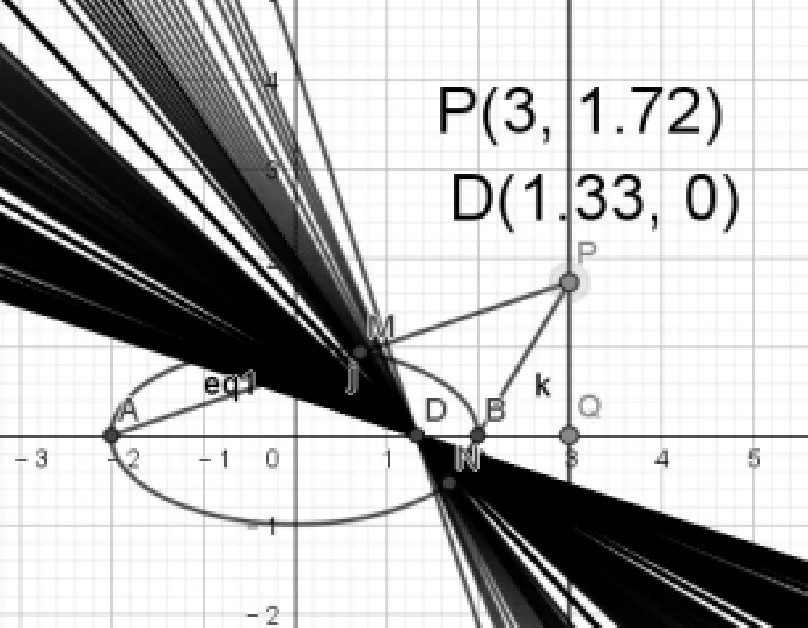
图1

图2

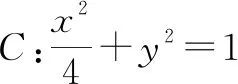
(2)椭圆的特征量影响直线所过定点.

①通过拖动滑动条改变短轴的长度(如图3，图4)，学生发现直线MN始终过定点D(1,0)，从而得到结论：椭圆的特征量b不影响直线MN所过的定点.

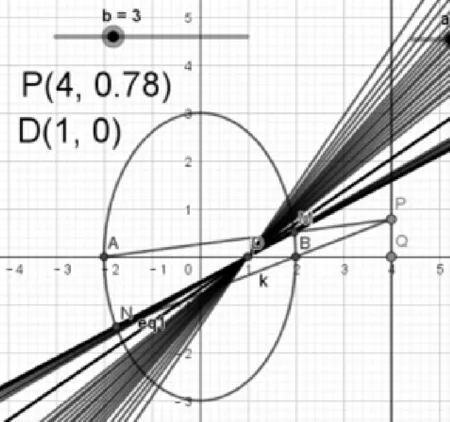
图3

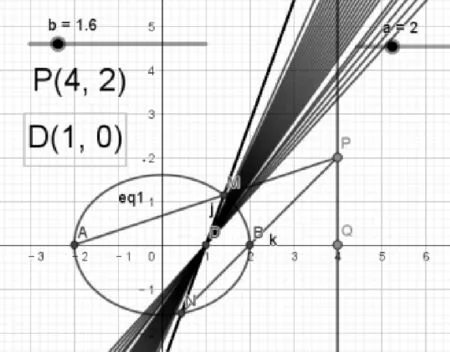
图4

②通过拖动滑动条改变长轴的长度(如图5，图6)，学生发现直线MN所过定点随着特征量a的改变而改变，但只要将特征量a确定下来，直线MN就会经过某一个定点.学生进一步探究特征量a与定点D坐标之间的关系，通过记录数据，分析数据关系，得到如下结论：

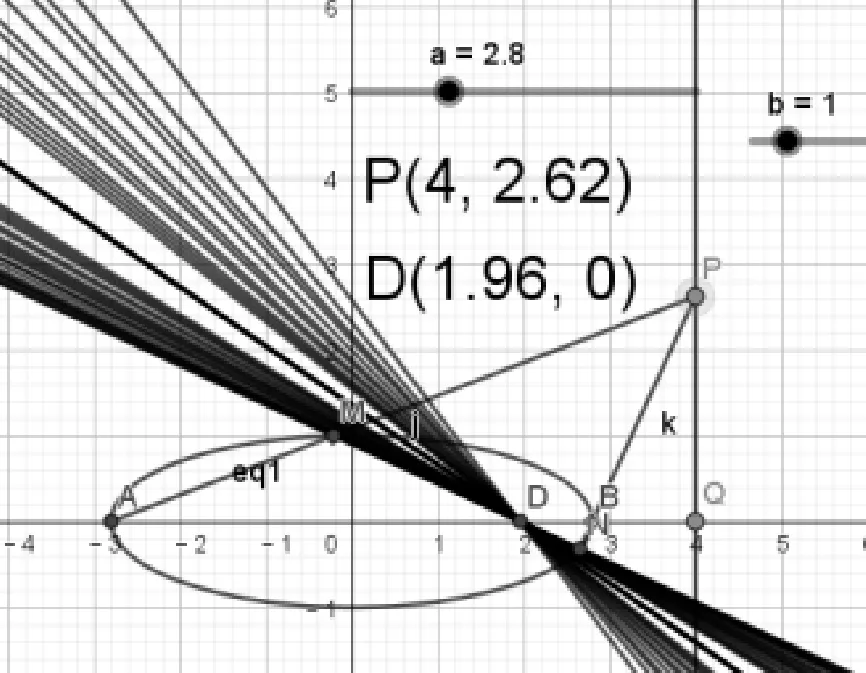
图5

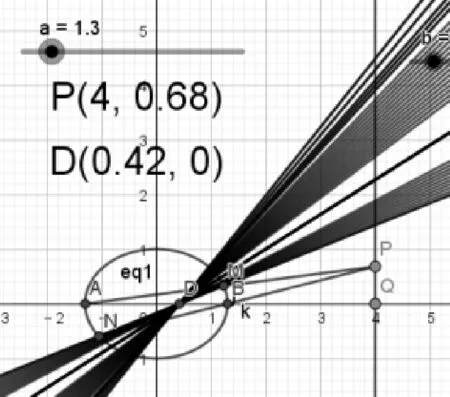
图6

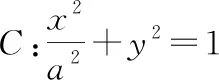
综合上述两组实验，学生最终能够提炼出下述数学结论：

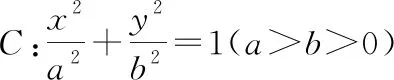
(3)点A,B在椭圆上的位置影响直线所过定点.

学生通过改变点A,B在椭圆上的位置，发现点A,B位置的改变会影响直线MN所过定点，然而暂时没能得到类似上述“完美”的结论.不过这个探索过程对学生来说非常宝贵，学生在“试误”的过程中，不断修正自己的想法，有利于锻炼数学思维，有利于形成积极探索的学习态度，可以初步感受自主学习和开展研究的一般方法，为形成终身学习的习惯奠定基础.

设计意图：本环节学生借助GeoGebra进行“可视化”实验探究，让静态数学“活”起来，激发学习兴趣和探究欲望.学生通过操作软件观察问题背后呈现的规律，大胆猜想数学结论，进行合情推理，经历由特殊到一般发现问题的过程.整个探究活动以自主思考和同伴互助的形式展开，既有独立学习的过程，又有群体学习的过程，既培养学生的自主探究意识，也培养学生的合作交流意识.本环节充分体现学生的主体性、实践性，学生在具体的情境中思考、探索，积累科学研究的经验.

环节三：发散思维，提出问题.

思考：根据上述实验探究发现的结论，你能尝试从其他角度提出新的解析几何问题吗？

在本环节中，学生根据探索发现结论，小组合作探讨，设计出了很多精彩的问题，现举例如下：

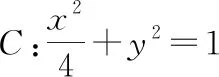
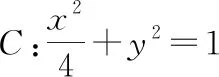
设计意图:学生根据实验探究得到结论“xDxP=a2”，自然地由定点问题生成定值问题.本环节旨在给学生创造机会，站在命题人的角度设计新的问题，培养从数学角度发现问题、提出问题的能力.在提出问题的过程中，培养学生的高阶思维能力和创新精神，提高学生的数学学习水平.

环节四：课堂小结，拓展提升.

小结：请谈谈在本次探究活动中你的收获有哪些？还有哪些困惑？

思考：(1)请在上述设计的问题中自主选择1～2个进行严格代数推理；

(2)如果将引例中点P所在的直线x=4换成y=4或者更一般的直线y=kx+b，借助GeoGebra，你能得到类似上述的结论吗？请自主设计方案，完成实验探究；

(3)对于双曲线、抛物线，你能得到类似的定点定值吗？借助GeoGebra，自主设计实验方案，完成实验探究.

设计意图：总结本节课的实验过程，帮助学生积累研究数学问题的基本思路和方法，为后续自主探究奠定基础.

3 结束语

(1)应用GeoGebra开展数学探究活动，可以使抽象的数学知识更加生动形象，使复杂问题“可视化”.例如，在函数专题利用GeoGebra探究三次函数的切线问题等；在立体几何专题利用GeoGebra探究正方体的截面图等；在解析几何利用GeoGebra探究圆锥曲线中运动变化问题等；在概率统计专题利用GeoGebra进行数据分析等.

(2)应用GeoGebra开展数学探究活动，有助于活跃课堂氛围，提高学生参与课堂的积极性，构建以学生为主体的深度学习环境.学生可以经历发现问题、提出问题、解决问题的过程，训练思维的深度和广度，培养创新意识和能力.同时，可以缩短学生自主探究的时间，降低探究难度，切实提高自主学习能力和效果.

(3)应用GeoGebra开展数学探究活动，从教师的层面要创设恰当的问题情境，引导学生合理使用信息技术，把握数学探究的自主度.如果教师给了学生探究的机会，却采取高度控制的方式，学生将只能做一些低级思维的操作性活动；而自主度适当的活动学生会更主动地调动头脑中的知识和经验，建立知识间的联系，实现有意义的学习，涵育核心素养[4].