基于高阶思维的单元教学设计研究——以平面解析几何为例

⦿云南师范大学 彭先琦 孔德宏

1 问题提出

为响应2014年教育部发布的《关于全面深化课程改革落实立德树人根本任务的意见》，落实“以人为本”的基本教学理念，《普通高中数学课程标准(2017年版)》(后文简称课标)凝练了六大数学核心素养，其中高阶思维是数学核心素养体系的关键[1].学生高阶思维的形成建立在对问题的深度研究与知识的本质把握之上，同时对教学设计提出了更高的要求.当前，我国数学教材采用章节化的编排体系，存在知识点之间逻辑不清晰，章节内在联系不深入等问题.其中，泸教版和人教版数学教材的 “平面解析几何”部分都存在小节内容之间衔接不连贯、公式推导与学生认知逻辑有差距等问题[2].在这一背景下，本文中提出基于高阶思维的单元教学设计研究.

2 高阶思维的生成机制

高阶思维指利用高阶规则在环境中求解问题的一种认知策略，其中高阶思维活动具有主动的、意图的、建构的、真实的和合作的五个特性.了解高阶思维的生成机制有助于培养高阶思维，本研究对高阶思维生成机制的应用主要参照段茂君等提出的高阶思维生成的四个阶段[3]，具体生成机制如图1所示.

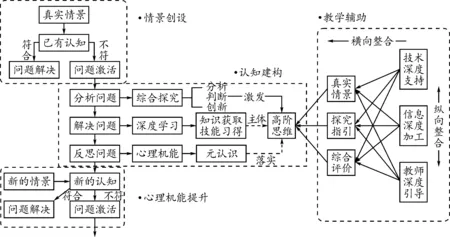
图1 高阶思维生成机制

阶段一：情景设置——激活问题.在真实情景中遇到不符合认知的元素从而激发思考，牵动高阶思维.该阶段是高阶思维生成的前提.

阶段二：综合探究——分析问题.运用分析、判断、创新等思维技能对问题进行分析.该阶段是高阶思维生成的基础.

阶段三：深度学习——解决问题.通过对问题的分析，概括新的知识或技能，进一步习得与掌握，提升高阶思维.该阶段是高阶思维生成的主体.

阶段四：心理机能——反思问题.在问题解决后，回顾整个过程，凝练问题解决的途径与方法，并运用元认知能力评估自身心理机能变化情况.该阶段是对高阶思维生成的巩固.

3 “平面解析几何”的高阶思维单元设计

“平面解析几何”位于课标选择性必修的“几何与代数”主题，《普通高中教科书数学·选择性必修一(A版)》第二章和第三章，内容包括：直线与方程、圆与方程、圆锥曲线与方程、平面解析几何的形成与发展(选修)[4].本次高阶思维单元设计基于高阶思维生成机制与单元教学设计原则，按照确定基本问题、设计学习活动、制定评估方式的顺序生成.

3.1 阶段一：确定基本问题

由于学生的高阶思维是在探究问题的过程中生成，因此单元教学设计应首先确定能引发学生对该单元本质思考的基本问题.基本问题设计需要考虑两方面内容：(1)关于学生认知，应考虑是否位于学生的最近发展区内及是否与已有认知产生冲突；(2)关于教学内容，是否能够体现与渗透本单元所包含的数学思想与核心素养.这两方面内容的确定依靠分析教学要素及确定教学目标.教学要素的分析应包括数学分析、课标分析、学情分析、教材分析、重难点分析、教法分析六个方面.以学情分析为例，应涵盖：(1)学生对平面解析几何的原有认知程度；(2)学生对圆锥曲线的了解程度；(3)学生对平面解析几何的情感态度；(4)学生学习平面解析几何的方法、习惯以及风格.教学目标在突出发展高阶思维的基础上从知识与技能、过程与方法、情感态度与价值观三个方面制定.基于上述分析，阶段一的详细设计如下.

(1)确定教学目标.

从现实和数学两个角度认识直线、圆、椭圆、双曲线和抛物线，掌握相应的几何特征与代数表达式；

能运用代数法和几何法判断上述五类方程的位置关系，并能求解相关的几何数值；

能够运用平面解析几何解决一些数学问题或现实问题；

能根据问题情境，建立合适的直角坐标系；

掌握代数几何化与几何代数化的方法与技巧；

体会与感悟平面解析几何中蕴含的数学思想.

(2)确定基本问题.

为什么需要平面解析几何？

如何进行平面解析几何的研究？

平面解析几何中几何与代数有哪些联系？

圆锥曲线的价值是什么？

代数法和几何法各自有什么优势与弊端？

3.2 阶段二：设计学习活动

根据高阶思维生成机制，结合已确定的基本问题，从情景认知、综合探究、深度学习、心理机能四个方面对学习活动的主要环节设计如下.

(1)情景设置.

目的：通过情景设置引导学生提出相关数学问题，激发学生主动思考，提高学生的学习兴趣.

环节：

了解解析几何的数学史；

了解阿波罗尼乌斯研究中介绍三种曲线与圆锥曲线的联系；

了解航天器飞行轨迹与椭圆之间的联系；

利用工具探究圆锥曲线的现实意义；

了解圆锥曲线在现实中的应用，如航天器飞行轨迹、通风塔等.

(2)综合探究.

目的：通过设置探究活动，培养学生团队协作能力，激发学生高阶思维.

环节：

学生分别运用和不运用平面直角坐标系研究物体运动轨迹；

探究确定直线的最少要素有哪些？分别可以组成几组？

探究椭圆参数对椭圆的影响与椭圆扁平程度的决定因素；

探究双曲线渐近线的方程；

判断二次函数、平抛运动是否是抛物线？为什么？

(3)深度学习.

目的：总结探究活动成果，得出数学概念或原理，并在相关问题中创造性使用，提高学生高阶思维.

环节：

总结直线、圆和圆锥曲线的定义、方程与性质；

利用代数法求解几何中的位置、距离、对称、角度等问题；

利用几何法求解直线、圆及圆锥曲线的方程.

(4)心理机能.

目的：激发学生元认知能力，总结深度学习成果，巩固学生高阶思维.

环节：

分析直线在代数和几何之间是如何联系的；

根据问题情境选择合适的代数方程；

创造性地将代数法和几何法进行结合；

总结如何简便地实现直线、圆及圆锥曲线的几何特征与代数特征的相互转换；

总结如何根据问题情境最大化使用代数法和几何法.

基于高阶思维培养的单元教学，对阶段二的设计需注意以下两个问题：(1)课程内容设置是否能体现大单元的核心思想与培养相应的能力；(2)课程进度设置是否与学生认知发展相适应.设计的基本思路为：(1)通过追溯平面解析几何的历史再结合初中相关的学习，介绍什么是平面解析几何并渗透其核心思想，体会学习与掌握平面解析几何的必要性；(2)在初中对直线与圆的认知基础上，深化其教学，初步培养学生将几何问题转化为代数问题，再从代数分析中提炼出几何性质的思想与习惯；(3)从现实与数学两个角度进行学生未接触过的圆锥曲线教学，在这一过程中帮助学生建立几何与代数更加紧密的联系，深化点与坐标一一对应的思想；(4)反思与总结所学知识，提炼出平面解析几何所渗透的数学思想并考察自身心理机能的变化情况.

3.3 阶段三：制定评估方式

高阶思维贯穿整个学习过程，因此制定评估方式应从不同方面进行综合评估，本文中选择探究活动成果、随堂检测、课题汇报、观察与谈话、课后作业、单元测验、自我评价与反思七种方式进行，具体内容见表1.其中，评估内容的设置应主要针对：(1)能够解决数学、其他学科和现实生活中相关问题的能力；(2)将数学作为交流工具的能力；(3)将数学作为一种推理方式的能力.评估内容应基于以下原则：(1)问题有非单一的答案；(2)问题的解决需要许多概念；(3)问题可以用很多方法来解决.这些原则旨在让学生多维思考问题，而非单一思维.使用几个概念来解决问题的目的是让学生运用所学知识，建立知识联系，从而获得解决方案.

表1 评价体系

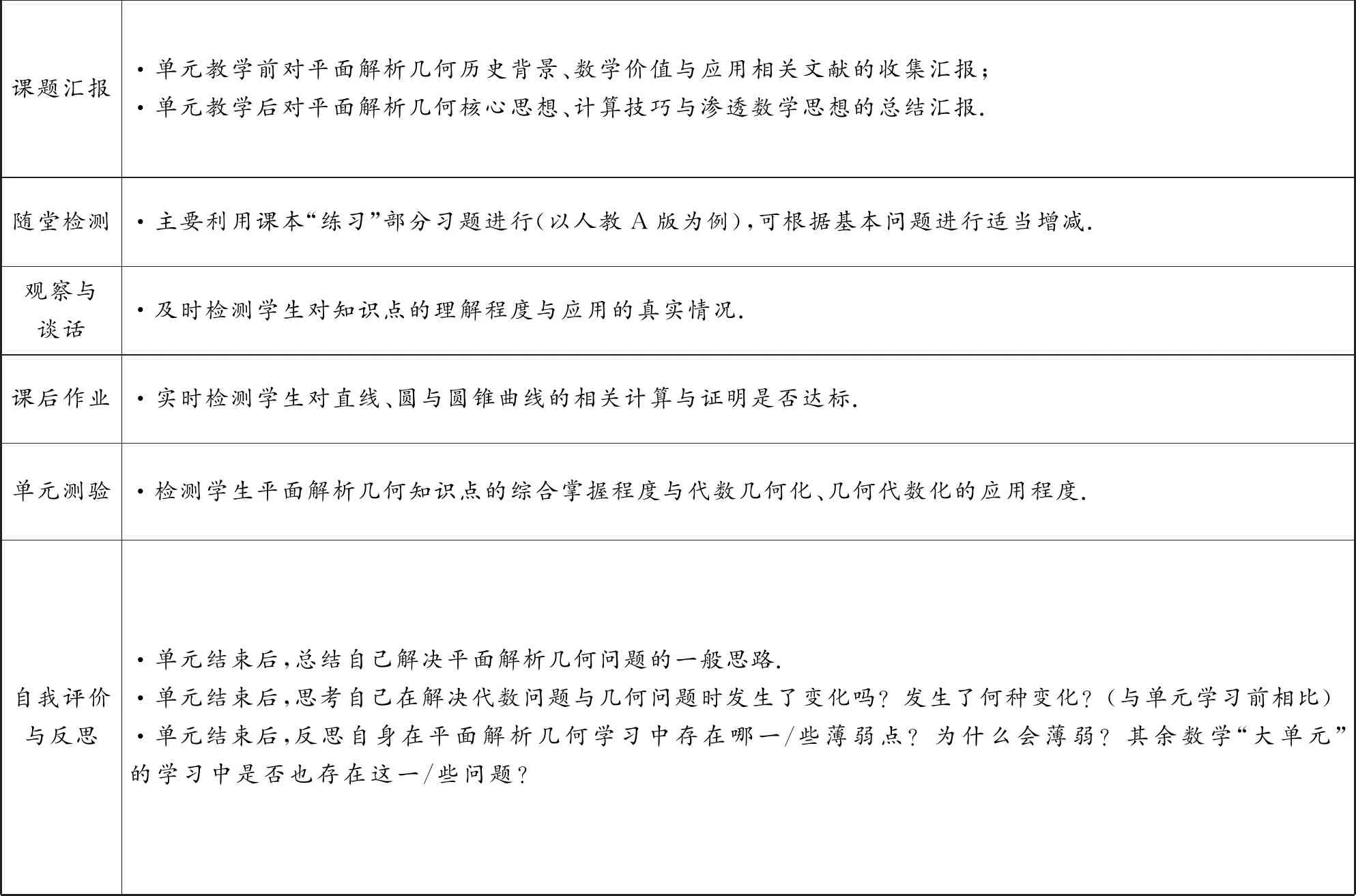
(续表)

4 总结

基于高阶思维的单元教学设计的特点为：(1)在传统教学设计的基础上依据高阶思维生成机制将教学活动分为情景认知、综合探究、深度学习、心理机能四个模块，加强对学生高阶思维的开发与培养；(2)在此过程中将“大单元”的核心思想融入整个教学设计，以包含“大单元”核心思想的基本问题驱动整个单元教学，有利于教学实施的连续性与一致性；(3)深度落实学生的数学核心素养,高阶思维是数学核心素养体系的关键，而发展数学核心素养是培养高阶思维的落足点.