具有媒体报道和时滞效应的SEIR模型动力学分析

刘志华， 曹 慧

(陕西科技大学 数学与数据科学学院, 陕西 西安 710021)

0 引言

随着信息技术的快速发展和进步,媒体报道对控制疾病传播起到了积极的作用,以2020年全球暴发的新冠疫情为例,媒体就疫情数据的实时报道引发了人们自觉关注疫情动态并做出相应的防护措施来保护自身,如勤洗手、少出门、远离密集人群等等.

近几年来,已有不少学者借助动力学模型研究媒体报道对疾病传播的影响[1-6].本文将讨论媒体报道对肺结核传播的影响.

事实上,肺结核存在明显的潜伏期,并且在潜伏期内,感染者没有不具有传染性,也不出现症状,很难被发现.一旦感染者因某种原因导致免疫力下降就会发病成为肺结核病人.肺结核病人有症状和传染性,易于发现.而真正影响人们的是被媒体所报道出来的出现症状的发病人数.因此,给出以下模型

(1)

其中:Λ是人口的常数输入率,β是发生率,d是自然死亡率,μ是因病死亡率,α表示潜伏感染者的发病成为肺结核病人的发病率,γ表示肺结核病人的恢复率.e-εE(t-τ)表示t-τ时刻的肺结核发病人数在t时刻被媒体报道后导致疾病传染率下降的作用因子,所有参数均为非负常数.令N(t)表示t时刻的总人口数,即,N(t)=S(t)+E(t)+I(t)+R(t).

1 模型分析和基本再生数

1.1 模型的适定性分析

本小节将先分析系统(1)解的存在唯一性和非负有界性,并给出其基本再生数.

定理1给定初值φ∈C+,则对所有的t>0,模型(1)存在唯一的且非负有界的解Xt.

证明：对于任意初值φ=(φ1,φ2,φ3,φ4)∈C+,定义

f(t,φ)=

其中f(t,φ)在(t,φ)∈R+×C+中是连续的,且函数f(t,φ)在C+的每个有界子集满足Lipschitz条件,根据Hale给出的定理[7],可知模型(1)在区间t∈[0,σ],σ∈R+上存在唯一解.

假设φi(0)=0,则fi(t,φ)≥0,依据文献[8]里的定理5.2.1和注释5.2.1,可知对于t∈[0,σ],解Xt具有非负性.

将模型(1)中的四个方程相加,可得

(S(t)+E(t)+I(t)+R(t))′=

Λ-dN(t)-μI(t)≤Λ-dN(t).

所以,有

这意味着

Γ=

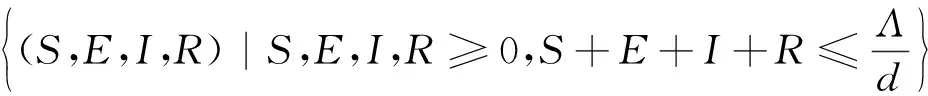
是模型(1)的正不变集.

证毕.

由于变量R没有出现在模型(1)的前三个方程里,因此可将模型(1)简化

(2)

显然,模型(2)与模型(1)有相同的动力学性态.在下面的分析中,将主要讨论模型(2).相应地,模型(2)的正向不变集为

其中Lambert W(·)是一个w→wew的复值函数[9].

1.2 基本再生数

利用再生矩阵的方法[10]可得到模型(2)的基本再生数

2 平衡点的稳定性

2.1 无病平衡点的稳定性

定理2如果R0<1,那么模型(2)的无病平衡点P0是全局渐近稳定的；如果R0>1,那么P0是不稳定的.

证明:模型(2)在P0处的Jacobia矩阵为

可见,λ1=-d<0是一个特征根,另外两个特征根满足方程

λ2+(d+α+d+μ+γ)λ+(d+α)(d+μ+γ)(1-R0)=0.

这表明当R0<1时,P0是局部渐近稳定的.反之,R0>1时,P0是不稳定的.

下面,证明无病平衡点的全局稳定性.令Lyapunov函数V1(t)=αE(t)+(d+α)I(t),则V1(t)沿着模型(2)的解的全导数为

V1′(t)|(2)=αβe-εE(t-τ)SI-(d+α)(d+μ+γ)I≤

αβSI-(d+α)(d+μ+γ)I≤

αβS0I-(d+α)(d+μ+γ)I=

(d+α)(d+μ+γ)(R0-1)I.

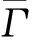
证毕.

2.2 地方病平衡点的稳定性

定理3如果R0>1且τ=0,那么模型(2)的地方病平衡点P*是全局渐近稳定的；如果R0<1,则P*是不稳定的.

证明:当τ=0时,模型(2)在P*处的Jacobia矩阵为

J(P*)=

其中

a=-ε(d+α)E*-(d+α),

L=(d+μ+γ)(d+α).

假设λi,i=1,2,3是矩阵J(P*)的特征根,满足Reλ1≤Reλ2≤Reλ3.注意到d-Λ/S*<0.进而可得detJ(P*)=(d-Λ/S*-dεE*)(d+α)(d+μ+γ)<0,所以λ1λ2λ3<0.自然对于λi,i=1,2,3的大小仅有两种情况：Ⅰ)Reλi<0,i=1,2,3；Ⅱ) Reλ1<0≤Reλ2≤Reλ3,易看出trJ(P*)<0,故可知λ1+λ2+λ3<0,由此得出Re(λ1+λ2)<0和Re(λ1+λ3)<0.

依据文献[11],J(P*)的二阶加性复合矩阵为

J[2](P*)=

直接计算可得

detJ[2](P*)=

其中

K=Λ/S*+ε(d+α)E*+(d+α)>0,L>0.

根据二阶加性矩阵的性质,J[2](P*)的特征根为λi+λj,1≤i1时,P*是局部渐近稳定的.

下面,证明地方病平衡点的全局稳定性.令Lyapunov函数

则V2(t)沿着模型(2)的全导数为

V2′(t)|(2)=

证毕.

3 Hopf分支的存在性

本小节将讨论当τ>0时,模型(2)在地方病平衡点处发生Hopf分支的充分条件.

3.1 Hopf分支的存在性

当τ>0时,模型(2)在平衡点P*处的Jacobia矩阵为

J(P*)=

其特征方程为

λ3+A2λ2+A1λ+A0+(B2λ2+B1λ+B0)e-λ τ=0.

(3)

其中

B2=ε(d+α)E*,

B1=ε(d+α)(d+d+μ+γ)E*,

B0=dε(d+α)(d+μ+γ)E*.

且Ai>0,Bi>0,i=0,1,2.令λ=iω(ω>0)为方程(3)的纯虚根,代入可得

(4)

因此

进一步有

ω6+p3ω4+p2ω2+p1=0,

(5)

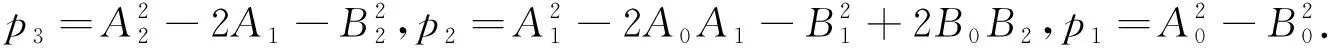
令x=ω2,则方程(5)被重新简化为

F(x)=x3+p3x2+p2x+p1=0.

(6)

(7)

下面,给出Reλ(t)对τ求导的sign大小.

定理4

证明:将方程(3)的左右两边分别对λ和τ进行求导

因此

(8)

另外,λ=iω(ω>0)是方程(3)的纯虚根,那么iω必满足如下等式

|(iω)3+A2(iω)2+A1(iω)+A0|2=

|B2(iω)2+B1(iω)+B0|2

即

(9)

因此,利用等式(9),(8)式可简化为

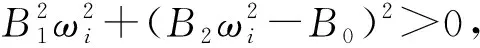
证毕.

3.2 实根的分布

本小节依据文献[3]中附录给出的一元三次方程证明,将直接给出方程(6)实根的存在条件.

F(x)=x3+p3x2+p2x+p1=0

则对于一元三次方程F(x),令

A=p32-3p2,

B=p3p2-p2p1,

C=p22-3p3p1,

Δ=B2-4AC.

引理1

(1)当Δ>0,且p1<0时,方程F(x)有且仅有一个正实根x,满足F′(x)>0.

(2)当Δ=0,且p3<0,p2=0,p1=0或p1<0时,方程F(x)有且仅有一个正实根x,有F′(x)>0.

(3)当Δ<0,且p2≤0或p3>0,p2>0,p1<0或p3<0,p2>0,p1≥0时,方程F(x)有且仅有一个正实根x,有F′(x)>0.

(4)当Δ<0,且p3<0,p2>0,p1<0时,方程F(x)有两个正实根xi,有F′(xi)>0,i=1,2.

(5)当A=B=0时,方程F(x)有三个重实根.

定理5如果R0>1,且

(1)满足引理1的(1),(2),(3)中任意一个条件,则模型(2)的地方病平衡点P*在τ∈[0,τ0)区间内是局部渐近稳定的；当τ>τ0时,P*是不稳定的,并且模型(2)会在P*附近当τ=τ0时经历Hopf分支.

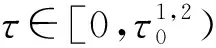
4 数值模拟

本小节将给出参数值,进行数值模拟,来补充证实理论的正确性.

对于模型(2),选取参数Λ=0.2,β=1,ε=6,d=0.1,μ=0.1,γ=0.1.则有R0=5.925 9>1.令初始值S0=0.5,E0=0.15,I0=0.1,S0+E0+I0≤Λ/d=2,利用Matlab计算可得地方病平衡点P*=(S*,E*,I*)=(0.767 5,0.136 9,0.365 2).

进一步有,Δ=-0.007 5<0,p2=-0.083 5<0.由引理1知,方程(6)存在一个正根ω1=0.242 3,再通过(7)式直接算得τ0=11.666 6,τ1=31.117 4.

给定初始值S0，E0和I0,当τ=8<τ0时，如图1中(a)、(b)图所示,模型(2)的平衡点P*是渐近稳定的.当τ=20>τ0时,如图2(a)、(b)图所示,模型(2)在平衡点P*附近发生Hopf分支,出现周期解.

随着τ的增加,模型(2)的平衡点由稳定变为不稳定,呈周期性变换,如图3所示.

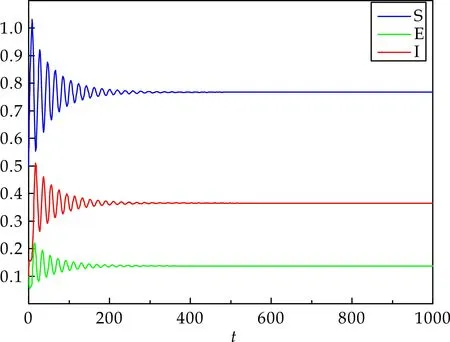
(a)时间序列图

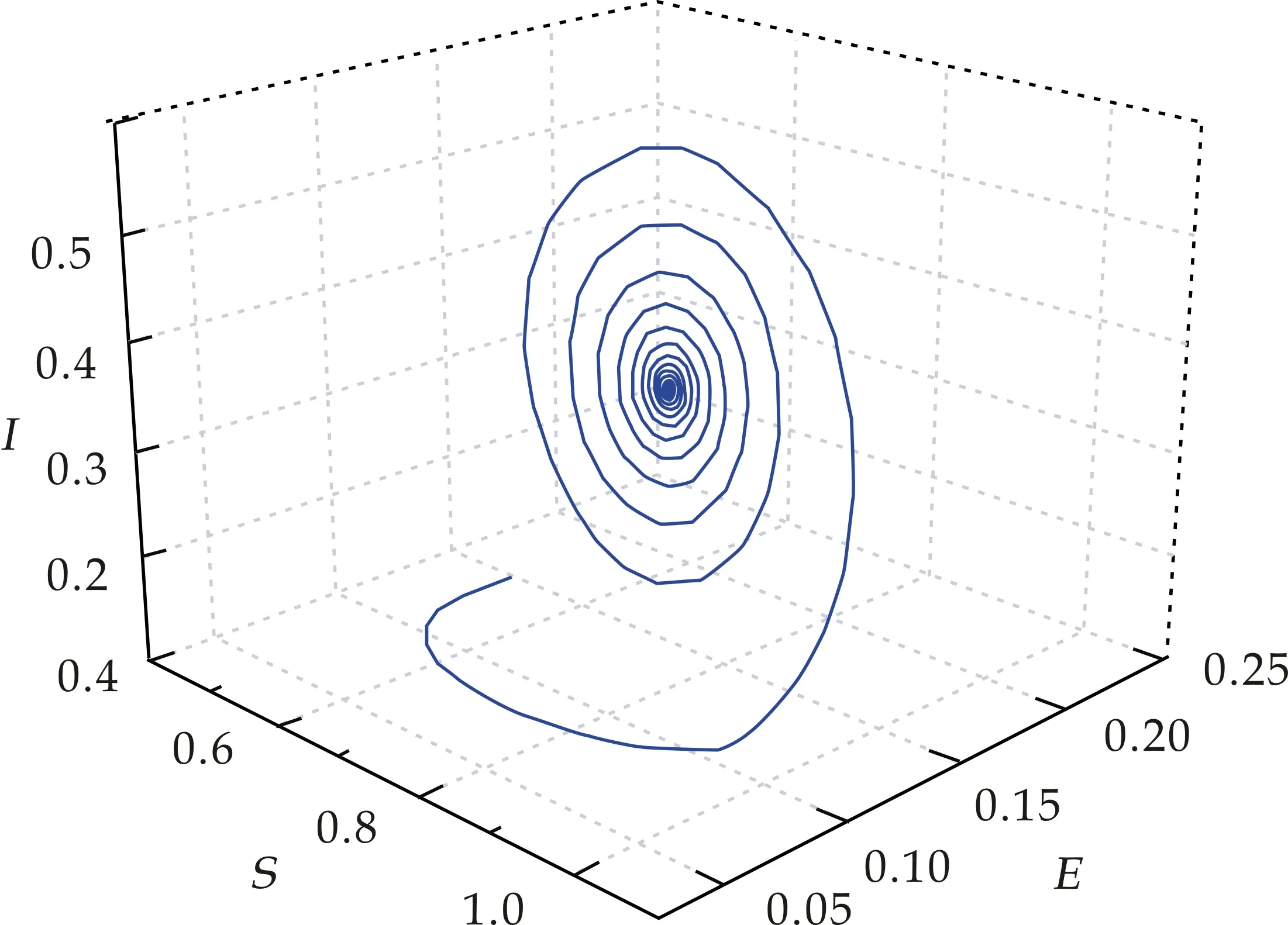
(b)相图图1 取τ=8<τ0时,模型(2)在平衡点P*处的时间序列图和相图

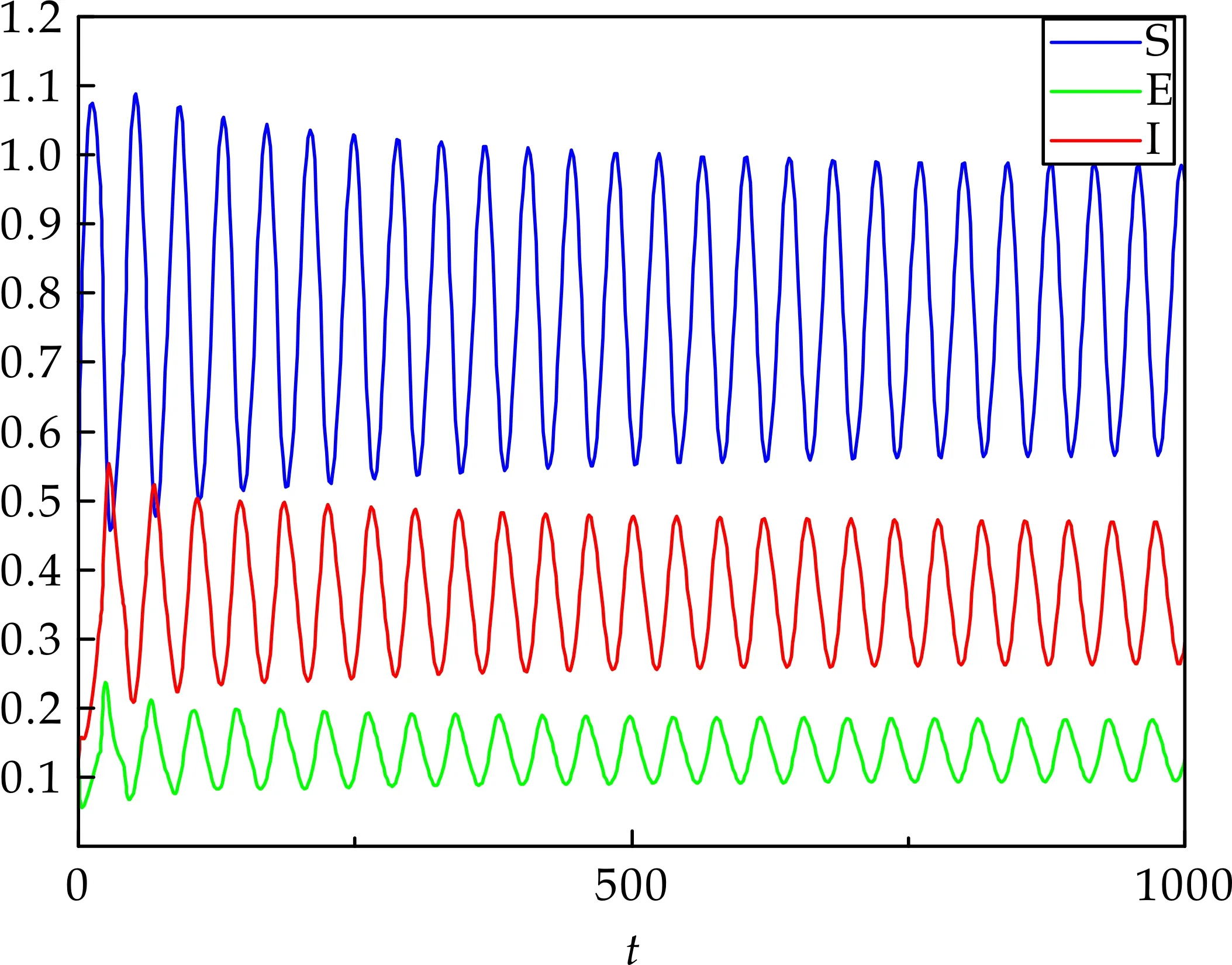
(a)时间序列图

(b)相图图2 取τ=20>τ0时,模型(2)在平衡点P*处的时间序列图和相图

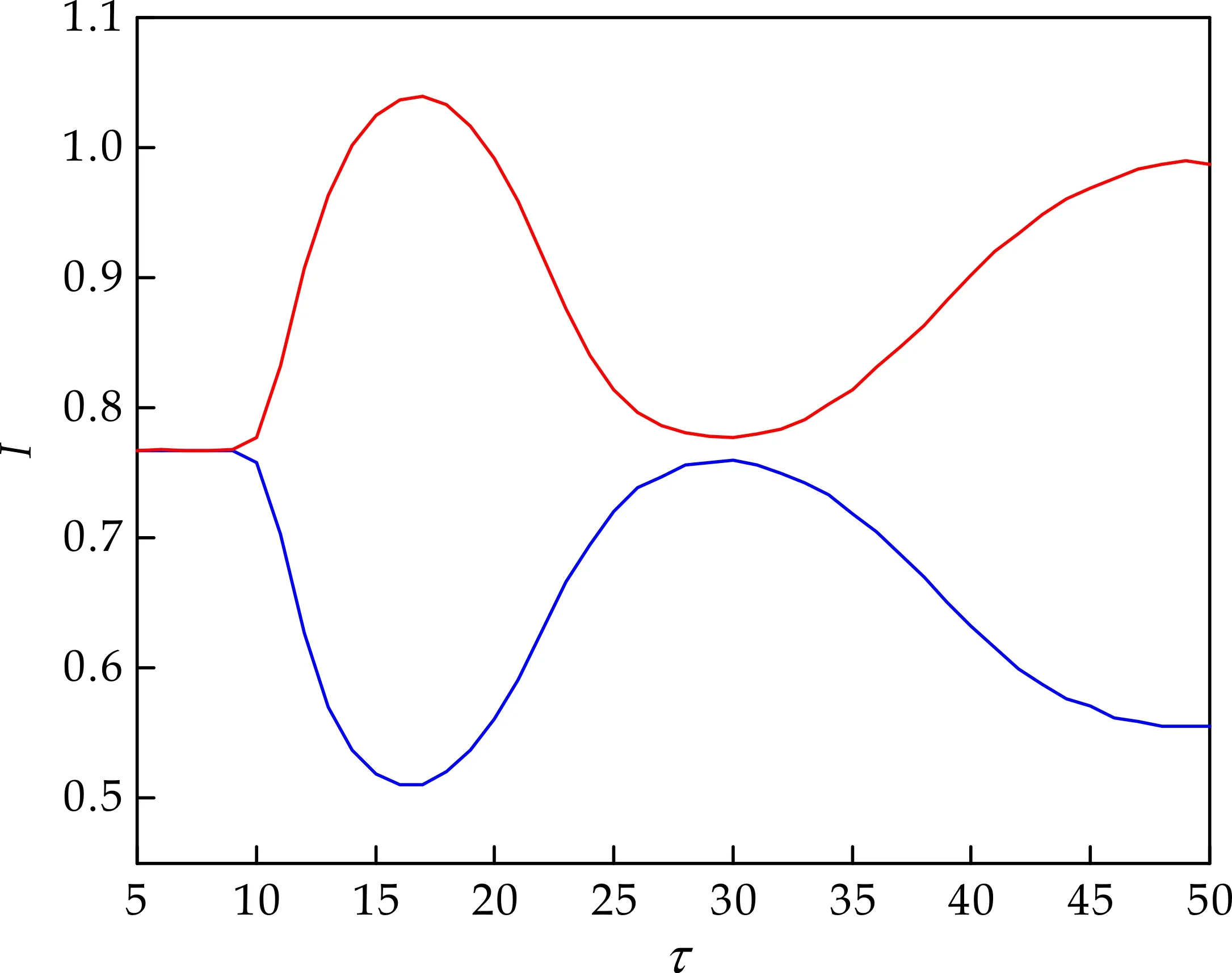
图3 随着τ的增加,描述模型(2)动力学的分岔图

5 结论

通过对SEIR模型的讨论,文章证明了当R0<1时,模型(2)的无病平衡点P0是全局渐近稳定的;当R0>1,τ=0时,模型(2)的地方病平衡点P*是全局渐近稳定的;当R0>1,τ>0时,P*不再稳定；进而,在满足引理1的条件下,当τ=τi,i=1,2,3…时,模型(2)会发生Hopf分支.

可见,媒体报道的作用因子e-εE(t-t)引起了模型(2)发生复杂的动力学性态,即,产生Hopf分支.