基于多特征信息融合与进化计算的碎片重组

党悦晨， 李 婉， 周 强*

(1.陕西科技大学 电气与控制工程学院 , 陕西 西安 710021; 2.陕西科技大学 电子信息与人工智能学院, 陕西 西安 710021)

0 引言

三维碎片的拼接重构对文物修复的相关工作具有重要的指导意义.通常的人工拼接不仅耗时耗力，且在碎片已经破损的基础上易造成二次破坏.随着科学技术的不断提高，利用计算机辅助进行文物碎片拼接的相关研究也在不断提升.

针对旋转体类器型碎片.欧阳磊广[1]与王坚[2]依据法向量拟合出旋转轴，进而计算出母线，基于轴对齐以及母线配准来实现拼接.但此类方法不适用于不存在旋转轴的非旋转体类器型.

针对具有参考模板的修复问题.高宏娟等[3]利用形状签名算法提取碎片与模板上的关键点，并计算特征直方图描述子，根据相似度构建匹配关系.Zhang K等[4]整合碎片与模板以及碎片与碎片之间的匹配情况，通过寻找全局一致性高的碎片组合实现对头骨碎片的拼接.但对于文物碎片，预先无法获取其完整器型，故对于模板的获取存在困难.

针对非薄壁类器型碎片的拼接.Huang等[5]基于体积积分不变量建立多尺度特征描述符并结合表面粗糙度，从完整碎片中分割出断裂面，通过特征区间聚类以及聚类重叠检测实现特征对应，提高匹配的鲁棒性.刘晓宁等[6]建立多尺度SURF特征描述符，通过计算Jaccard距离[7]得到最佳匹配.王飘等[8]使用Splatting lines生成碎片纹理特征线，进行基于纹理形状约束的初匹配以及基于断裂边缘的校准匹配.对于断裂区域面积较大的情况，常用点云配准来寻找碎片间的几何变换关系，例如ICP[9]、FPFH[10]、4PCS[11]、RANSAC[12]以及全局配准[13]等，但由于薄壁碎片断裂区域面积狭窄且相对平滑的特性，难以基于断裂面上的凹凸特征进行特征匹配，故上述方法均不适用.

针对表面具有显著沟壑的碎片，Papaioannou等[14]利用完整区域上线性结构，通过跟踪外推曲线来实现拼接.针对平面碎片，Derech等[15]提出边沿外推法对可能存在的磨损区域进行预测，通过计算相异度和置信度来确保碎片刚体变换的准确性.

针对薄壁文物碎片，王金梅等[16]提出样条插值曲线拟合的方法提取轮廓曲线，通过比较曲线的几何特征实现匹配.但曲线拟合的时间复杂度较高.蔺素珍等[17]与谭鑫刚等[18]通过筛选曲率局部极大值得到角点，计算角点间弦长，将碎片匹配转化为弦长序列匹配.但此类方法严重依赖角点获取的准确度，一旦错误角点被标记或真实角点被漏选，必然导致整体拼接的错误，故成功率存在一定局限.

现有研究，在针对陶瓷碎片这类即缺失纹理信息又包含薄壁器型难点的拼接领域略有空缺，难以实现高成功率以及高准确度的拼接.故本文提出基于边缘线的多特征提取与融合，全面且细致的对断裂区域轮廓进行量化，同时提出球体空间点共存检测算法用于评价碎片组断裂区域之间的拼接情况，设计进化计算基于全局迭代出最优拼合方案，避免错误回溯产生的高时间复杂度.该方法通用性广，不局限于器型的对称性以及厚度，可在无模板的情况下成功实现拼接精准度高的三维碎片拼接重构.

1 基于多特征信息融合的曲线表示

本文以三角网格模型为研究对象，通过匹配断裂区域轮廓线，进而实现碎片间拼合.因此，本节针对薄壁器型提出基于多特征提取与融合的断裂区域轮廓线量化表示.通过提取基于曲率半径向量的初级特征以及深度特征，结合挠率特征，将抽象的轮廓线实现量化，在表征空间几何结构特征的同时，对方向变化趋势进行预测.从而克服单一描述量难以具体以及全面的表征曲线独有特征，而导致出现大量相似片段，增加后期筛选工作量以及算法时间复杂度的问题.同时，本文使用一维特征序列作为最终的表示形式，降低数据维度，增加算法效率.

1.1 曲率半径特征

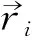
(1)对于一组由边缘轮廓点连接而成的线段L=(P1,P2,…,Pn)，其中轮廓线段顶点Pi=(xi,yi,zi)，i=1,2,…,n，n为所包含断裂边缘顶点个数.对于待计算位置顶点Pi，提取其前后相邻两个位置顶点Pi-1与Pi+1.

(2)根据三个空间点共面，确定平面约束方程：

根据三个空间点到圆心坐标距离相等，确定距离约束方程：

将两个约束方程联立，得到圆心空间坐标的线性代数方程：

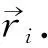
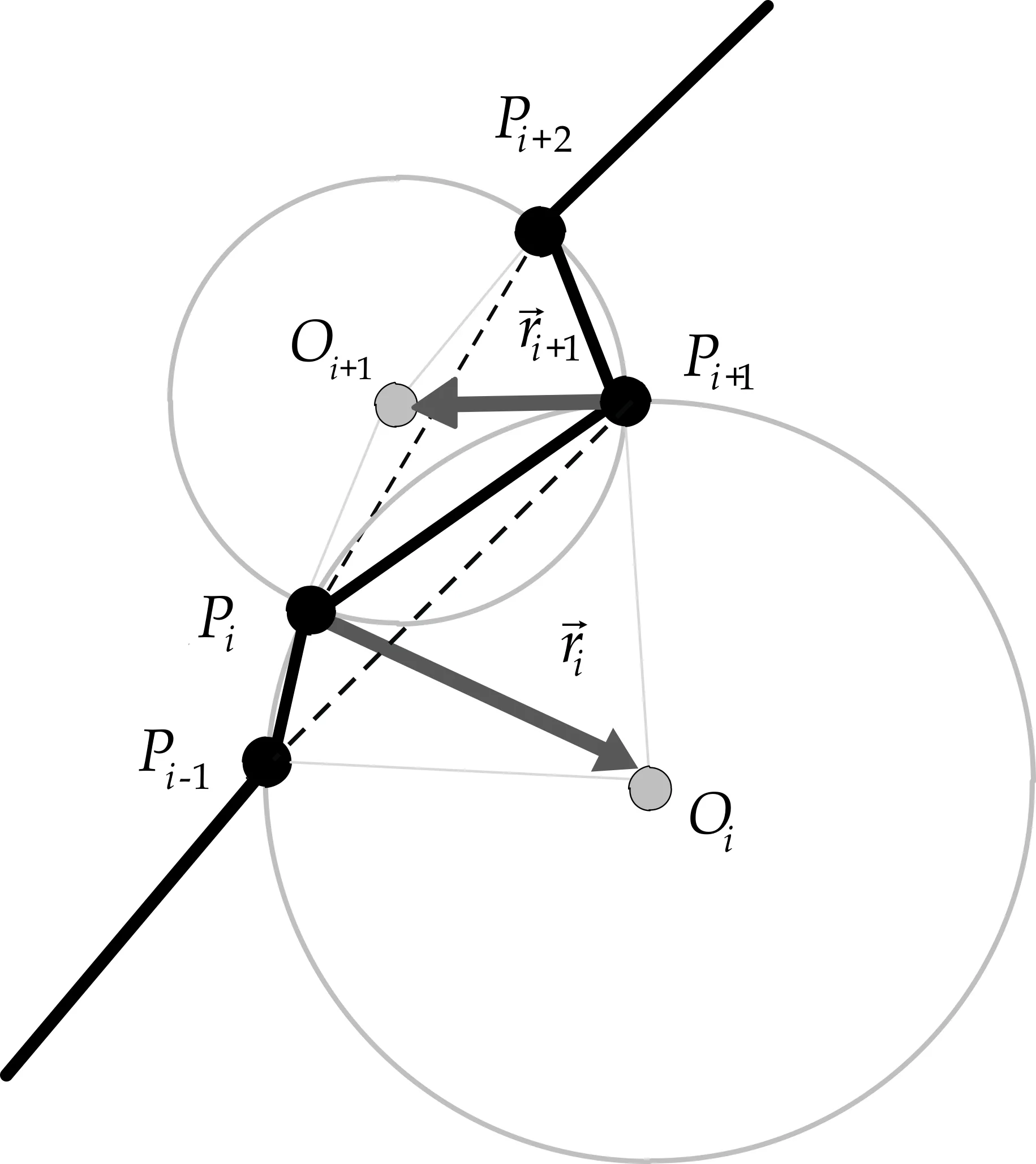
图1 曲率半径向量

曲率特征描述量一：曲率半径向量模值.

针对边缘曲线上的每一个顶点计算出曲率半径向量，再对向量进行模值计算,如式(1)所示，从而得到该断裂边缘的曲率半径集合r，即r={r1,r2,…,rj,…,rn}作为初级特征，该集合反映了曲线的弯曲程度，描述出边缘轮廓的局部平面几何结构.

(1)

曲率特征描述量二：曲率半径向量变化.

针对断裂边缘曲线的曲率半径向量集合，计算出相邻向量间的变化向量，再进行模值计算，如式(2)所示，从而得到该断裂边缘的曲率变化趋势集合rΔ，即rΔ={rΔ1,rΔ2,…,rΔj,…,rΔn}，作为深度特征，通过深层次分析三维曲线弯曲程度，实现了对断裂边缘曲线变化趋势的预测.

(2)

1.2 挠率特征

挠率即曲线上邻近两点的次法向量之间的夹角对弧长的变化率，代表曲率平面的扭曲程度.将挠率作为特征量应用于轮廓线的描述，可以更加准确地反映出曲线的空间结构.

针对三维离散曲线难以拟合参数方程的问题，本文采用微中心差分算法[22]，以离散曲线的目标点为中心，进行局部范围内的逐阶差商计算，即:

一阶差商：

二阶差商：

三阶差商：

其中k1、k2和k3为邻域半径，即每阶差商目标点单侧需要上一阶差商值的个数.

根据所得各阶差商，带入到挠率计算公式(3)中，即得到离散曲线上各点处的挠率τ(t).

(3)

挠率特征描述量：

针对断裂边缘曲线上的每一个顶点，使用微中心差分算法，得到相应的挠率特征集合τ，即τ={τ1,τ2,…,τi,…,τn}，该集合反映曲率平面扭曲程度，描述出三维曲线的空间几何结构.

1.3 边缘轮廓的多特征融合与量化表示

多组特征描述量之间相互独立，分别从不同衡量角度对三维曲线进行表征.为了降低分批次比对特征带来的时间复杂度，同时方便于匹配段的搜索，本文提出多特征融合与量化表示的方法，将多组特征按权值进行融合，从而得到边缘线的总特征描述集合f，其表示形式即f={f1,f2,…,fi,…,fn}，实现将多目标分次比较问题转化为单目标问题.再对曲线进行等间距采样并赋值，将其转化成一维特征序列的形式，从而同时反映出某一特征描述所对应的片段长度，将后期的碎片匹配转化为特征序列的比对，降低了数据维度，提高了算法效率.最终形式即：

Cf={f1,…,f1,f2,…,f2,fi,…,fi,fn,…,fn}

表示过程如图2所示，其中特征序列所包含的连续元素值相同的个数即表征为所对应边缘线段的长度.截取部分轮廓线的多特征量化结果如图3所示.

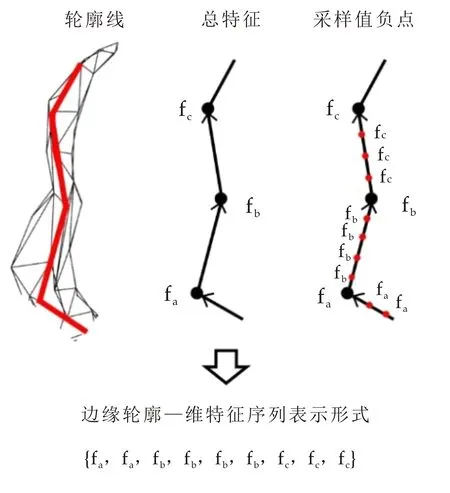
图2 一维特征序列表示过程

图3 边缘轮廓的多特征量化

2 碎片组间拼接与度量

对于相互独立的碎片，需要建立出碎片间的相互依赖关系.本文首先通过特征比较与匹配寻找出两个碎片之间的相似匹配段，并通过几何变换实现两两匹配拼接.再次，提出球体空间点共存检测算法，设立评价指标对两两拼接的结果进行评分.

2.1 碎片组匹配与拼接

通过动态比较匹配的方法，以采样点为单位移动特征序列，进行特征相减得到特征差值序列.标记差值连续小于阈值的最长片段为最佳匹配段，并以其特征差值平均值作为匹配段的特征差值函数F(i,j)，用于度量匹配段间的误差.对于碎片组拼接，为避免欧拉变换多次计算旋转角所带来的时间复杂度，本文基于罗德里格斯旋转公式，高效以及高精度的实现碎片组之间的变换.

R=I+sin(θ)K+(1-cos(θ))K2

(4)

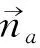
2.2 球体空间点共存检测算法

完成匹配拼接的碎片组，在实际情况下不一定为相邻碎片，因为存在边缘线相似度十分高，但实际毫无关联的碎片.对于此类情况，拼接后会呈现错位、空隙以及重叠渗透问题.故本文提出球体空间点共存检测算法，针对拼接后的结果，进行局部重叠检测，从而度量出拼接贴合程度，并设置阈值，区分出真正匹配组与伪匹配组.拼接贴合度对后期全局拼接也有十分重要的作用.算法步骤如下：

Step1：计算断裂边缘轮廓相邻顶点间的距离，记录距离最小值dmin.

Step2：设定小序号碎片为A，大序号碎片为B;提取A碎片上第i个断裂边缘顶点Pi，i=1,2,…,n,n为所包含断裂边缘顶点个数.

Step3：以Pi为球心，以dmin为半径，建立球体.

Step4：对B碎片上的断裂边缘顶点依次进行检测，当检测到其包含在所建立球体区域内，则停止检测，标记Pi为1；若遍历B碎片全部顶点，且未发现满足条件者，则标记Pi为0.

Step5：判断是否i=n，若是，则转至step 6；若否，则i=i+1且转至step 2.

Step6：统计A碎片被标记的顶点个数，即为该碎片组的拼接贴合程度M(i,j).

球体空间点共存检测算法原理如图4所示，正确拼合碎片组以及伪拼合碎片组之间的拼接贴合度差异十分明显，图中所示情况包含的点共存个数分别为36与6.针对不同形状的碎片类型，可通过改变球体半径dmin的比例系数来进行相应的调整，得到更加准确的评价.

通过本文所提出算法，可以准确的实现对两碎片拼合优劣的度量，成功地区分出正确拼合碎片.

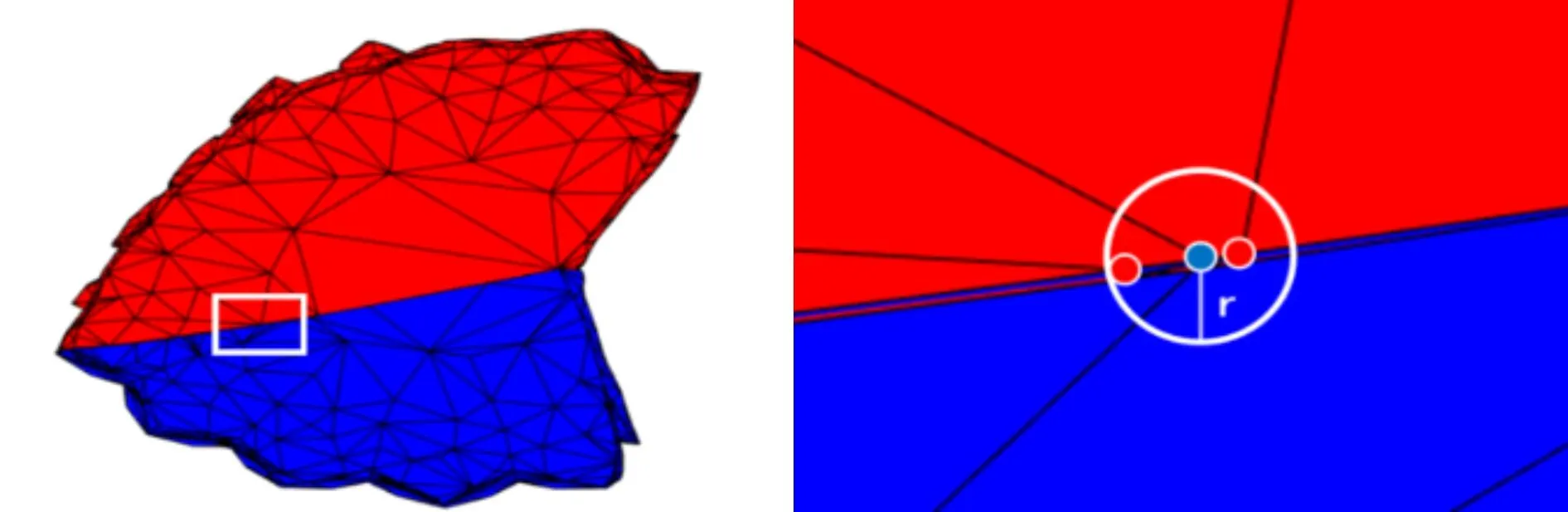
(a)正确拼合碎片组 (b)正确拼合局部图

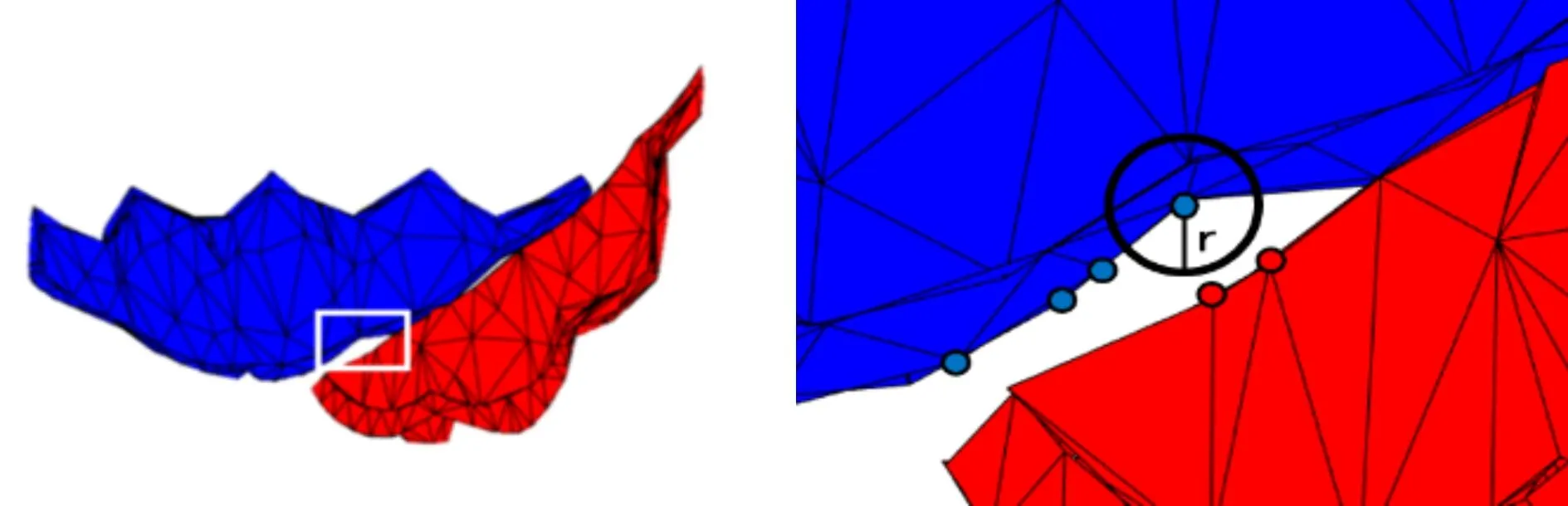
(c)伪拼合碎片组 (d)伪拼合局部图图4 球体空间点共存检测算法原理图

3 基于进化计算的全局拼接

碎片最终拼接，需要基于两两匹配结果选出可以组成完整器型的碎片组.作为非确定性多项式问题，穷举法的时间复杂度十分高，且若通过传统算法寻找局部最优解直接进行拼接，则又会导致较高的回溯率.针对这一问题，本文提出一种基于进化计算的全局拼接，以“优胜劣汰”的方式从全局出发寻找适应度最高的匹配方案.算法总流程图如图5所示.

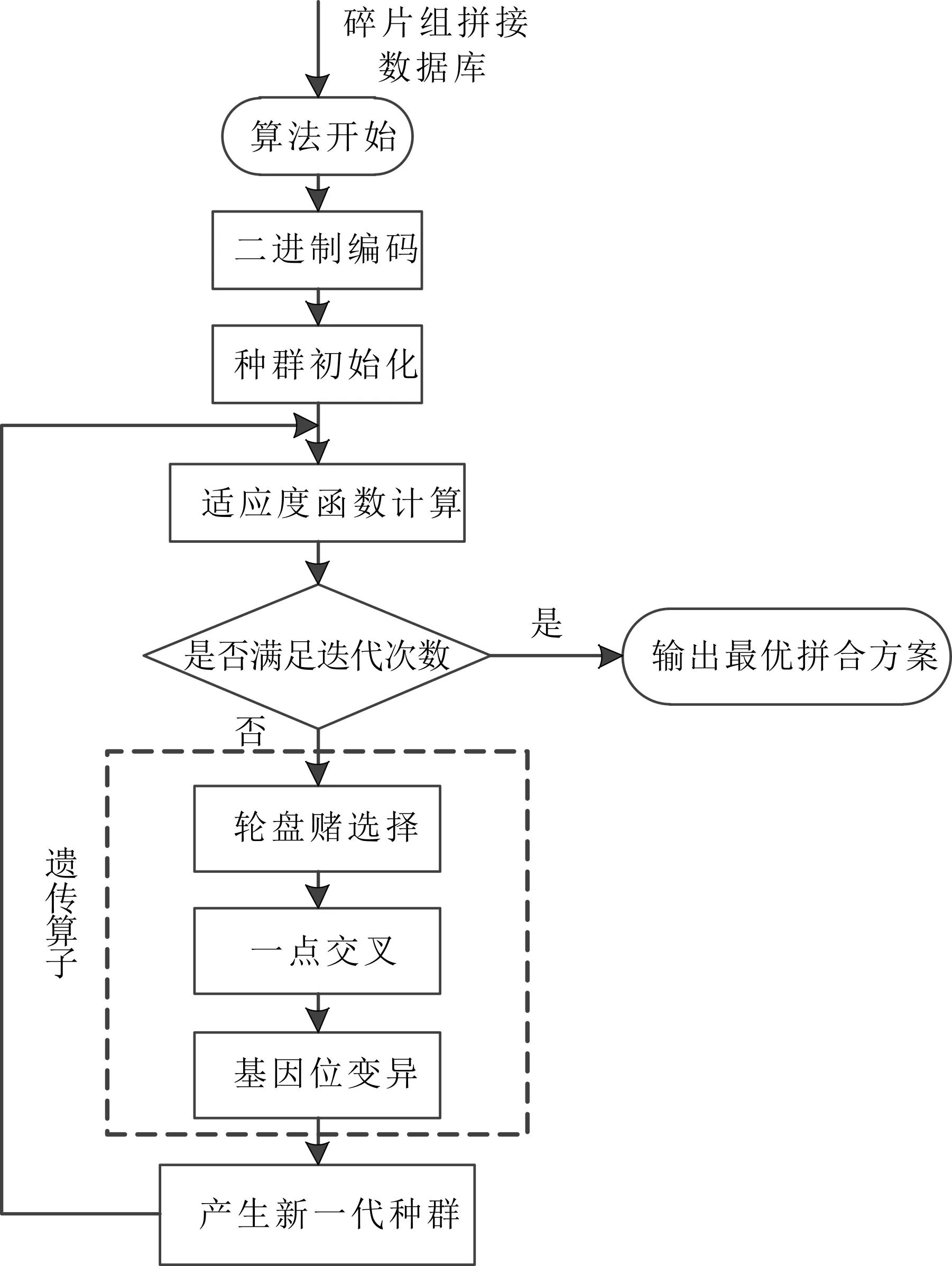
图5 进化计算总体流程

3.1 编码方式

因碎片形状的不规则性以及碎裂位置的随机性，无法使用传统方法中个体表示拼接顺序的编码方式.故针对碎片组拼接结果，利用二值符号集合{0,1}表示两两拼接组合的选取与否，得到更加灵活的编码方式.

待拼接碎片总数目为x，设置种群大小为m，染色体长度为n，随机生成m×n的矩阵即为种群.种群中第1号染色体上的基因序列表示为公式(5)：

chr1={g(1,2),g(1,3),…,g(i,j),…,g(x-1,x)}

(5)

其中

截取某个体部分编码片段如图6所示.

图6 个体编码示意图

3.2 适应度函数确立

进化计算运行时，不需要利用外部信息，通过判断种群中个体的适应度值来实现搜索.作为个体性能的评价指标，适应度函数在“优胜劣汰”过程中发挥着重要的作用，同时决定着算法的收敛速度以及能否得到最优解.

本文适应度函数的设计，由2.1节所得到的拼接贴合度M(i,j)，结合特征差值函数F(i,j)以及豪斯多夫距离H(i,j)构成，得到多目标优化问题，再通过加权和，转化为单目标问题，如式所示(6)，其中λ,μ和υ为三个评价参数相应的权值系数，用于将其转化为同一数量级，本实验所使用的初始化参数设置为[1,10,0.1]，具体可根据实际拼接效果适当调整.

υ×M(i,j))

(6)

通过本文所设计的适应度函数，可以全面的对个体进行评价，有效地完成最优个体的搜索，同时实现快速收敛.

3.3 全局拼接

在解空间进行寻优的过程，要求行为具有随机性与趋势性，从而在深度搜索与广度搜索中实现平衡.选择算子负责深度搜索，进行信息积累.交叉算子和变异算子负责广度搜索解空间中新的区域.

选择算子作为实现“优胜劣汰”思想的具体实施步骤，本文采用轮盘赌选择法.即在每一次的迭代过程中，结合个体的适应度函数，计算出其累积概率，从而分配被选中概率来进行选择.该方法在保证种群多样性的同时，使算法快速收敛至最优结果.交叉算子采用一点交叉.当条件满足交叉概率时，将相邻两个染色体从中间位置进行一点交叉，从而提高遗传算法的搜索能力.变异算子采用二进制变异.当条件满足变异概率时，随机选取染色体上任一基因位，对该位置的基因进行取反，保证种群的多样性.

按照所设置规则以及参数进行种群初始化，通过遗传算子的操作增加种群多样性，反复进行迭代.当迭代次数达到预设值或拟合收敛时，算法终止.

4 实验结果与分析

本文使用Matlab 2016b为仿真平台，在Intel(R) Core(TM) i9-9900k 3.36GHz内存为32GB的PC机上完成.实验对象为一组破裂的莲花碗器型碎片以及一组仿汝窑青瓷尊碎片.

4.1 碎片重组实验结果

针对实验碎片，部分碎片组间的匹配拼接与度量结果如表1所示.对全部碎片拼接组进行排列，按照表2设置进化计算参数，迭代过程如图7所示，最终拼接重构结果如图8所示.实验证明，本文所进行的算法研究，可以成功将破碎的三维碎片数据实现拼接重组，还原其完整的原始器型.

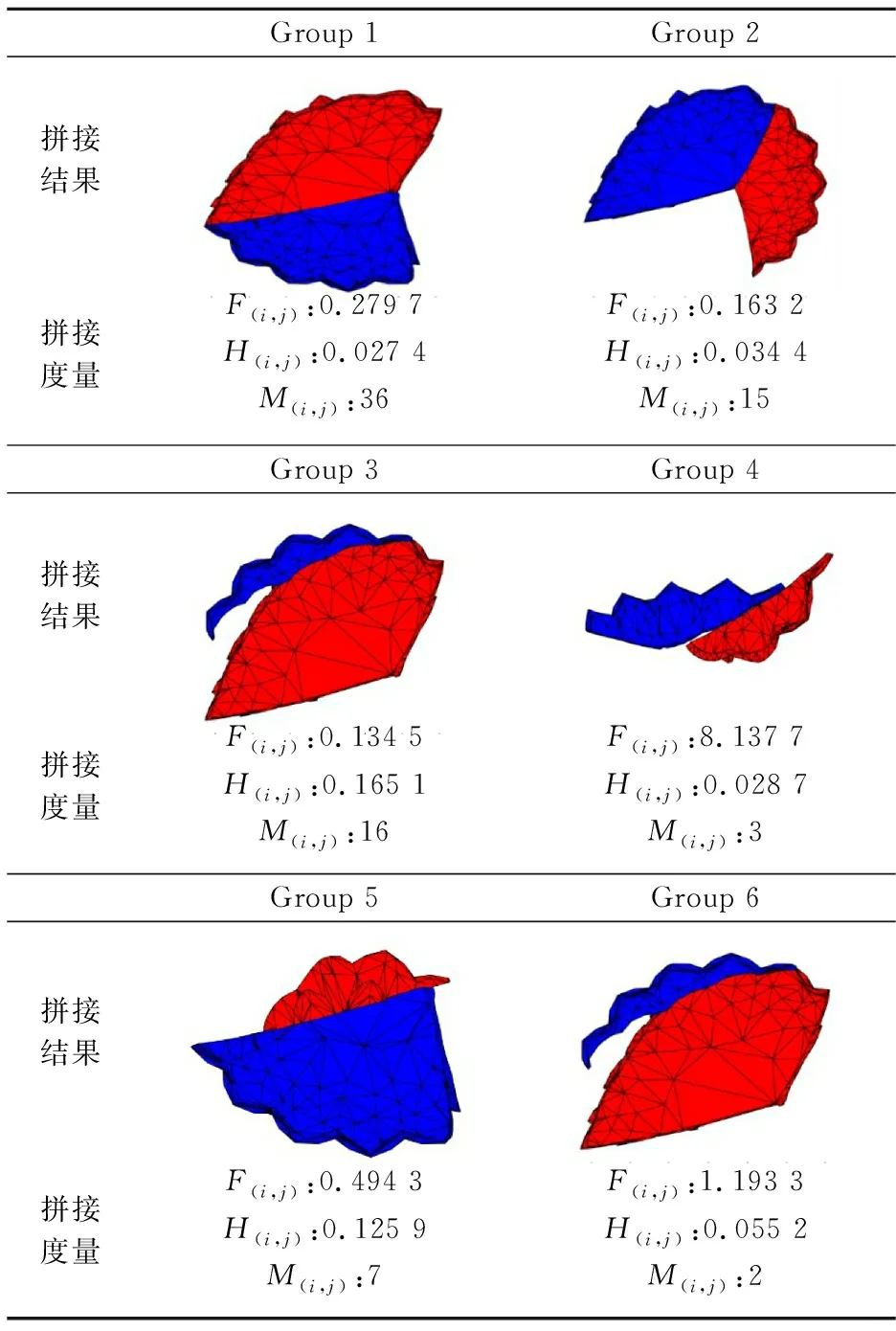
表1 部分碎片组匹配拼接

表2 进化计算参数设置

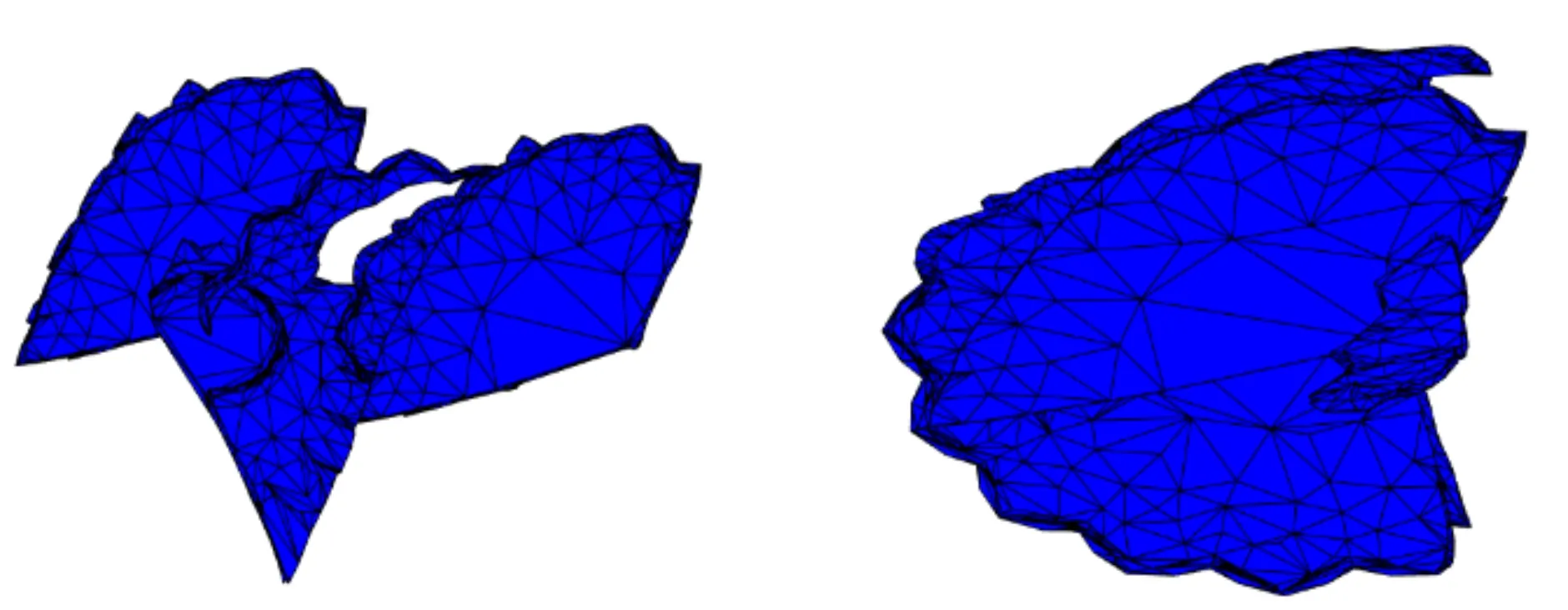
(a)Iterations:5 (b)Iterations:20

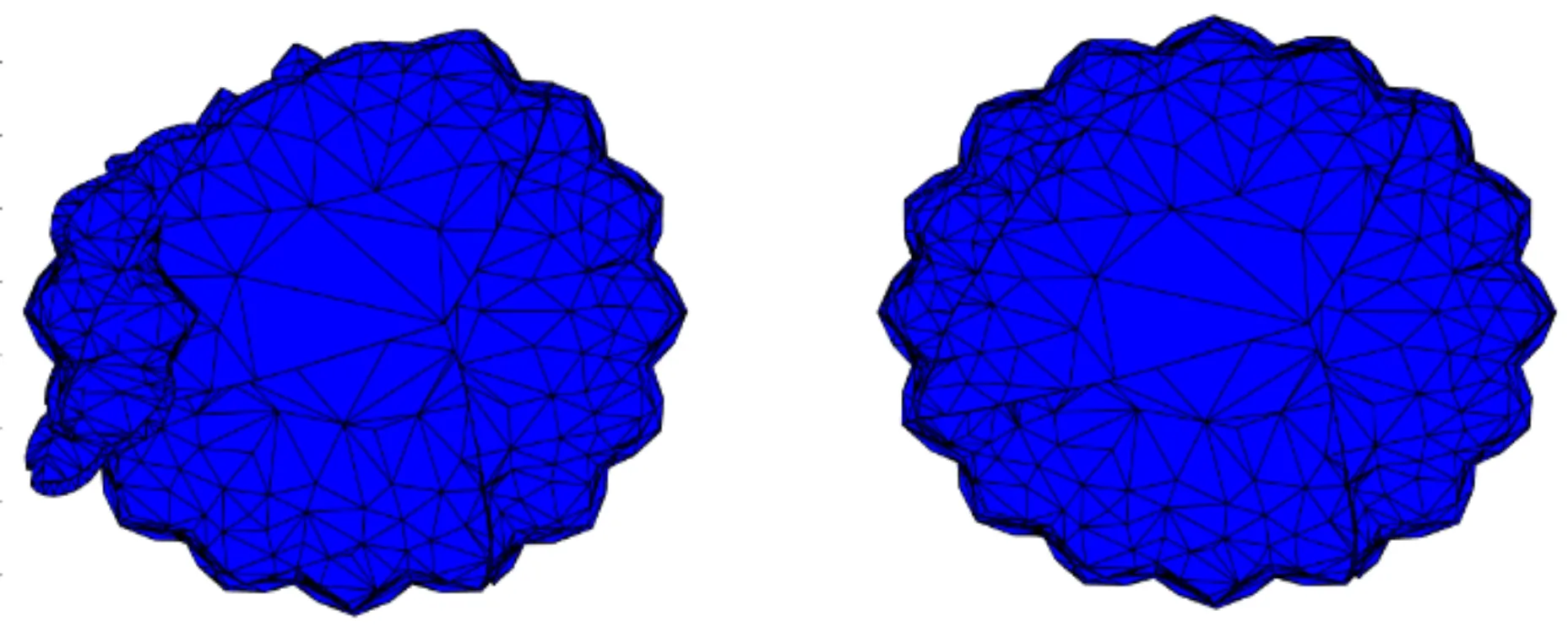
(c)Iterations:50 (d)Iterations:100图7 进化计算迭代过程

(a)莲花碗俯视图 (b)莲花碗侧视图

(c)青瓷尊俯视图 (d)青瓷尊侧视图图8 碎片重组结果

4.2 对比实验结果

方法一[24]：基于转向角特征边缘表示.

方法二[17]：基于曲率特征的边缘表示.

本文方法：基于曲率半径多级特征与挠率特征融合的边缘表示.

罐子器型碎片组拼接对比结果如图9所示.莲花碗器型重构对比结果如图10所示.

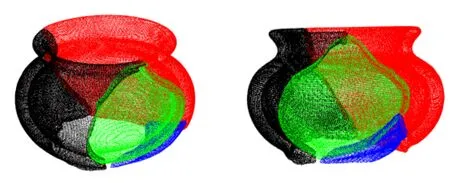
(a)方法一 (b)方法二 (c)本文方法图9 罐子器型对比结果

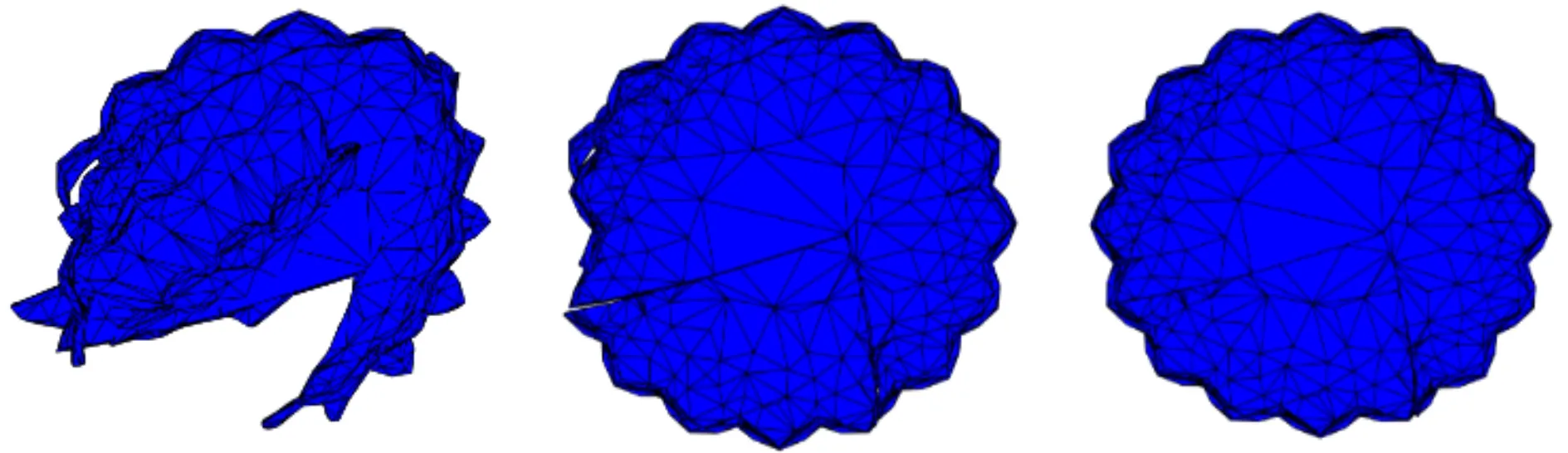
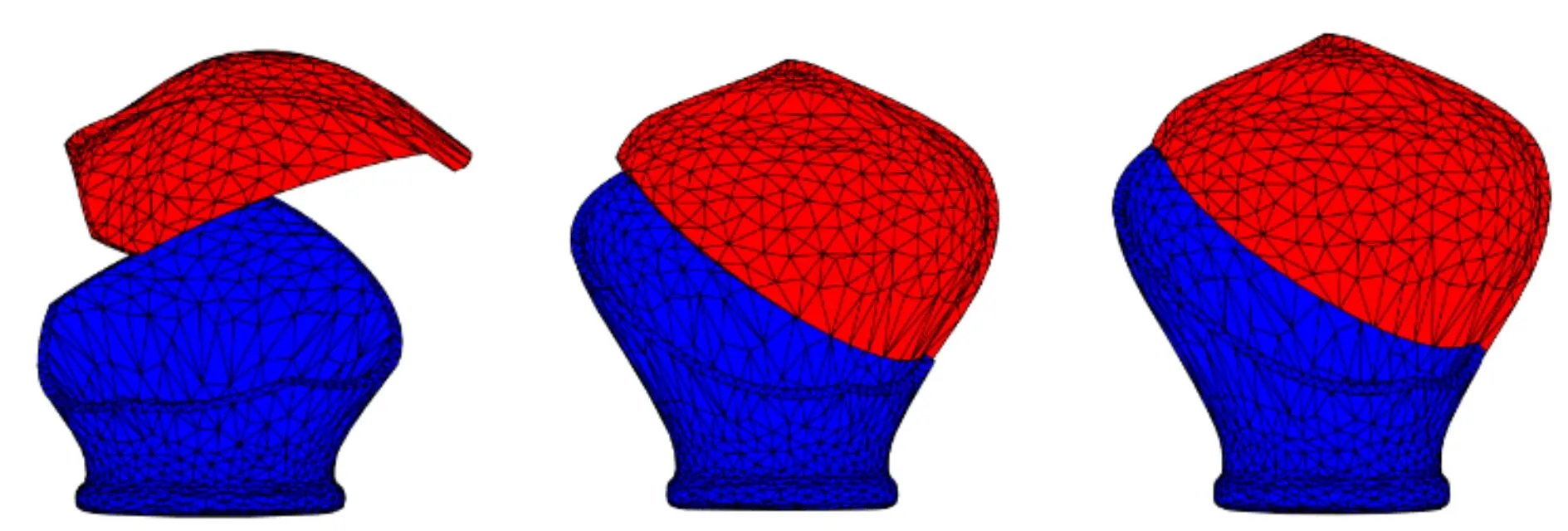
(a)方法一 (b)方法二 (c)本文方法图10 莲花碗器型对比结果

所对比方法的平均拼接准确率如表3所示，可以看出，本文所用方法在重构准确率上明显优于其它两种方法，针对薄壁器型可以更加具体以及全面的描述出边缘的个性化特征，区分出相似匹配段.

表3 不同方法拼接准确率比较

5 结论

本文工作的主要贡献如下：

(1)针对陶瓷碎片等薄壁类器型提出基于多特征信息融合与进化计算的碎片重组整体流程.克服薄壁碎片断裂面狭窄、规则且难以提取特征点的问题，实现由碎片到原始器型的还原；

(2)提出球体空间点共存检测算法，通过局部重叠检测对两碎片间拼接贴合度进行评价；

(3)在最终拼接阶段，引入进化计算，利用“优胜劣汰”的思想迭代得到基于全局的最优拼合方案.

实验结果表明，本文所提出的特征描述方法具有更高的拼接准确率，且通过进化计算避免了局部融合产生的回溯问题，提升拼接效率.同时算法适应范围广，可应用于多种碎片类型，十分有利于破损文物的复原工作.由于本文算法所采用了球体空间点共存检测策略，因此在进行拼接贴合度计算时较为耗时，如何进一步优化算法减少计算量，将是下一步研究的重点.