基于3D矩阵特征与多维卷积网络的脑电信号情感识别

陈景霞， 闵重丹， 林文涛， 郝 为， 刘 洋

(陕西科技大学 电子信息与人工智能学院， 陕西 西安 710021)

0 引言

随着人工智能的发展，如何让机器具有类似于人类的感知功能、思维能力和行为功能已经成为目前研究的热点问题，而情感计算技术在实现智能化人机交互时起着至关重要的作用.过往的研究主要是针对面部表情或语音信号进行情感识别，这些信号由于易于伪装而不能确定其客观性和有效性，且考虑到复杂的外部环境，机器不能够对伪装表情下的情绪进行精准识别.基于此，研究人员正努力尝试利用生理信号进行研究，比如皮肤电流、呼吸反应、眼电图、脑电图等等.相比于其他生理信号，脑电图信号(Electroencephalogram,EEG)能够反应中枢神经系统的动态变化且具有真实可靠的特点，目前已经被广泛应用于情感计算等研究领域.

在以往的研究中，许多研究者采用传统的机器学习算法进行情感识别，Kumar等[1]采用线性核最小二乘支持向量机(Linear kernel least squares support vector machines,LS-SVM)和反向传播人工神经网络(Back propagation artificial neural network,BP-ANN)，在效价与唤醒度模型上进行二分类情感识别，准确率分别达到61.17%和64.84%.Atkinson等[2]在标准脑电图数据集上，结合高效的特征选择方法和基于核的分类器对情绪进行分类，在SVM分类器上效价和唤醒度上的准确率分别达到了73.06%和73.14%.

目前，基于机器学习的情绪识别取得了一定成果，但由于传统机器学习方法相对简单，泛化能力不强，许多研究者将深度学习引入情感识别研究中并取得了一定成果.陈景霞在之前的研究中也有了重大发现，并提出了基于组合特征与深度卷积神经网络的脑电识别方法，比最佳的传统分类器集成决策树模型在效价和唤醒度上分别提高了3.58%和3.29%[3].还有研究者将深度学习与传统方法相结合，来提升情绪识别的准确率.

Wei等[4]提出了一种基于脑电图的情绪识别系统，用来识别积极、消极和中性三种情绪，该方法利用深度简单循环单元(Deep Simple Recurrent Units,DSRU)处理时间序列数据，解决了常规循环网络中长期依赖的问题，并采用三种不同的集成策略来集成基本SRU模型对情感进行分类，其分类精度达到了83.13%，比最佳的单个SRU模型高出了3.11%.

Nath等[5]分别采用了SVM和LSTM模型对脑电信号进行情感分类，依赖于被试的情况下LSTM模型在效价和唤醒度上准确率分别达到94.69%和93.13%，在独立于被试情况下SVM模型表现最好，在效价和唤醒度上准确率为72.19%和71.25%.

Pandey等[6]提出了一种基于脑电信号的被试独立情感识别技术，该方法利用变异模式分解(Variational Mode Decomposition,VMD)技术提取特征，利用深度神经网络作为分类器，从脑电信号中提取了与被试无关的脑电情感特征，实验结果表明，该方法在分类准确率上提高了约6.4%.

Yixin等[7]提出了一种区域自适应PSD矩阵网络(daSPDnet)，来捕捉不同主体之间共有的内在情感关系，利用分布自适应带来的特征自适应和质心比对实现样本自适应，并利用协方差矩阵计算PSD特征，该方法的情感分类准确率达到了82.67%.

Meiyan等[8]提出一种新的脑电地形图表示能量计算方法，用于解决来自多个主体和多个通道的高信噪比问题，使用卷积神经网络来学习大脑活动的脑电图模式，该分类方法的平均准确率比最佳的最新分类方法高出10.11%.

Chao等[9]将每个通道的原始生理信号转化为频谱图以获取时间和频率特征，再利用基于多模式注意力的BiLSTM从中自动学习最佳时序特征并输入到深度神经网络中，预测每个通道的情绪输出概率，并取得了较高的准确率.

尽管针对脑电情感识别的方法层出不穷，但是依然存在两个重要问题需要深入研究：一是如何获取脑电信号更优的特征表示方法.目前的脑电特征一般都采用一维链式特征来表示，忽略了多通道EEG信号间空间分布的增益信息.二是如何构建更有效的深层特征学习和情感分类的模型.传统的卷积神经网络未考虑到各个通道之间以及不同区域之间的相关性和交互作用.为了解决这两大问题，本文分别从特征表示和深度学习模型构建这两方面提出了新的方法.

1 3D矩阵特征表示与多维卷积网络的构建

一些研究人员发现，在提取手工特征时保留EEG电极的位置信息可以为情感识别提供增益信息[10].因此，如果可以在提取的情绪相关特征中保留电极位置信息，将有可能获得更好的识别性能.基于此，本文分别在频域和时域两个维度提取多个特征并进行拼接和维度转换，得到用3D矩阵表示的脑电特征，将其作为多维卷积神经网络的输入，经过多个不同维度的卷积级联进一步提取深度语义特征并进行情感分类识别.具体过程如下：

1.1 脑电时域和频域特征的提取

首先提取时域特征，假设每个通道的原始EEG信号表示为s(t),t=1,2,3,…,T，其中T表示信号的时长，总共有32个电极通道.对原始EEG信号分别提取以下6种特征：均值(μs)、方差(σs)、标准差(τs)、一阶差绝对值的平均值(δs)、二阶差绝对值的平均值(γs)和近似熵(ApEn)，计算公式分别如下：

(1)

(2)

(3)

(4)

(5)

近似熵(Approximate entropy,ApEn)[11]通常用一个非负的数字来量化时间序列的复杂性，其大小随着EEG时间序列复杂度的增高而增大，并且能够一定程度抑制噪声.对于EEG信号s(t)，定义阈值r用于相似度比较，然后确定子序列长度m(即窗口长度)，其中m为整数，r为实数.m通常选m=2或m=3，r的选择在很大程度取决于实际应用场景，通常选择r=0.2×std，其中std表示原序列的标准差，本文中设置m=2，r=0.2.

计算近似熵时，首先重构原始序列，将EEG信号s(t)转换为一组长度为m的向量序列，得到X(i)={s(i),s(i+1),…,s(i+m-1)}，其中i的取值范围为1≤i≤T-m+1.D{X(i),X(j)}表示X(i)与X(j)任意分量之间的欧式距离，并将各个分量之间最大距离定义为最大贡献成分距离，表示为：

D{X(i),X(j)}=max{s(i+k)-s(j+k)}

(6)

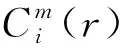
(7)

式(7)中：i满足1,2,…,T-m+1.再对其取自然对数，然后对所求的对数求其所有的i的平均值，用φm(r)表示：

(8)

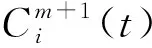
ApEn=φm(r)-φm+1(r)

(9)

在提取频域特征时，本文先对原始EEG时序信号在Delta(1 Hz～4 Hz)，Theta(4 Hz～8 Hz)，Alpha(8 Hz～13 Hz)，Beta(13 Hz～30 Hz)和Gamma(30 Hz以上) 五个频带上分别利用快速傅里叶变换提取频域特征，利用窗长为0.5 s的汉明窗对数据进行扫描，窗口挪动的步长设置为0.25 s，每滑动一次提取32个功率谱密度PSD特征，再将全频带上的PSD特征与五个分频带上的PSD特征进行连接，可得到6种不同的频域特征.由此，每个样本的时域和频域特征维度都是32(channels)×6.接下来，分别将时域与频域的6种线性特征转换成二维网状特征.

1.2 三维矩阵特征转换与表示

为了提取更具判别性的脑电特征，本文将一维链式EEG特征(即上述提取的多种时域和频域特征)转换为三维矩阵特征，该三维矩阵特征不仅获取了EEG信号在时域、频域的有效信息，更融合了不同电极间的空间位置相关信息，具体提取过程如下：

首先将一维脑电特征序列转换为二维网状结构.本文中使用32通道的EEG数据，32个通道分别为Fp1、AF3、F7、F3、FC1、FC5、T7、C3、CP1、CP5、P7、P3、Pz、PO3、O1、Oz、O2、PO4、P4、P8、CP6、CP2、C4、T8、FC6、FC2、F4、F8、AF4、p2、Fz和Cz.不同通道之间的位置和区域不同对各种情感的影响也不相同，理论上越相邻的两个电极之间的脑电信号越趋于相似.

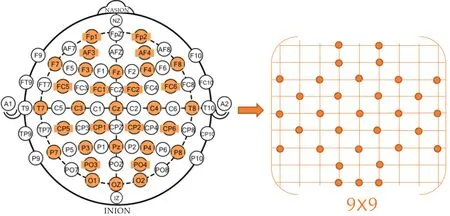
图1 32通道脑电信号所对应的二维网状矩阵

图1显示了特征维度变换时的映射关系.由图1可以看出，根据各个电极对应位置将脑电图映射成一个9×9的二维网状矩阵.为了保证空间信息完整且不影响其功能，使用0来填充映射矩阵的其他位置，矩阵中非0值表示对应通道的EEG特征值.将上述每种特征转换成一个9×9×1的特征矩阵，再分别将每个样本的6种时域特征和6种频域特征在第三维进行拼接，分别获得9×9×6的3D时域和频域特征矩阵，如图2所示.

3D矩阵特征不仅包含每个EEG通道的时域和频域特征，而且还保留了通道之间的空间相关信息，能够更直接准确地反映大脑皮层上EEG信号与情感相关的时空变化.

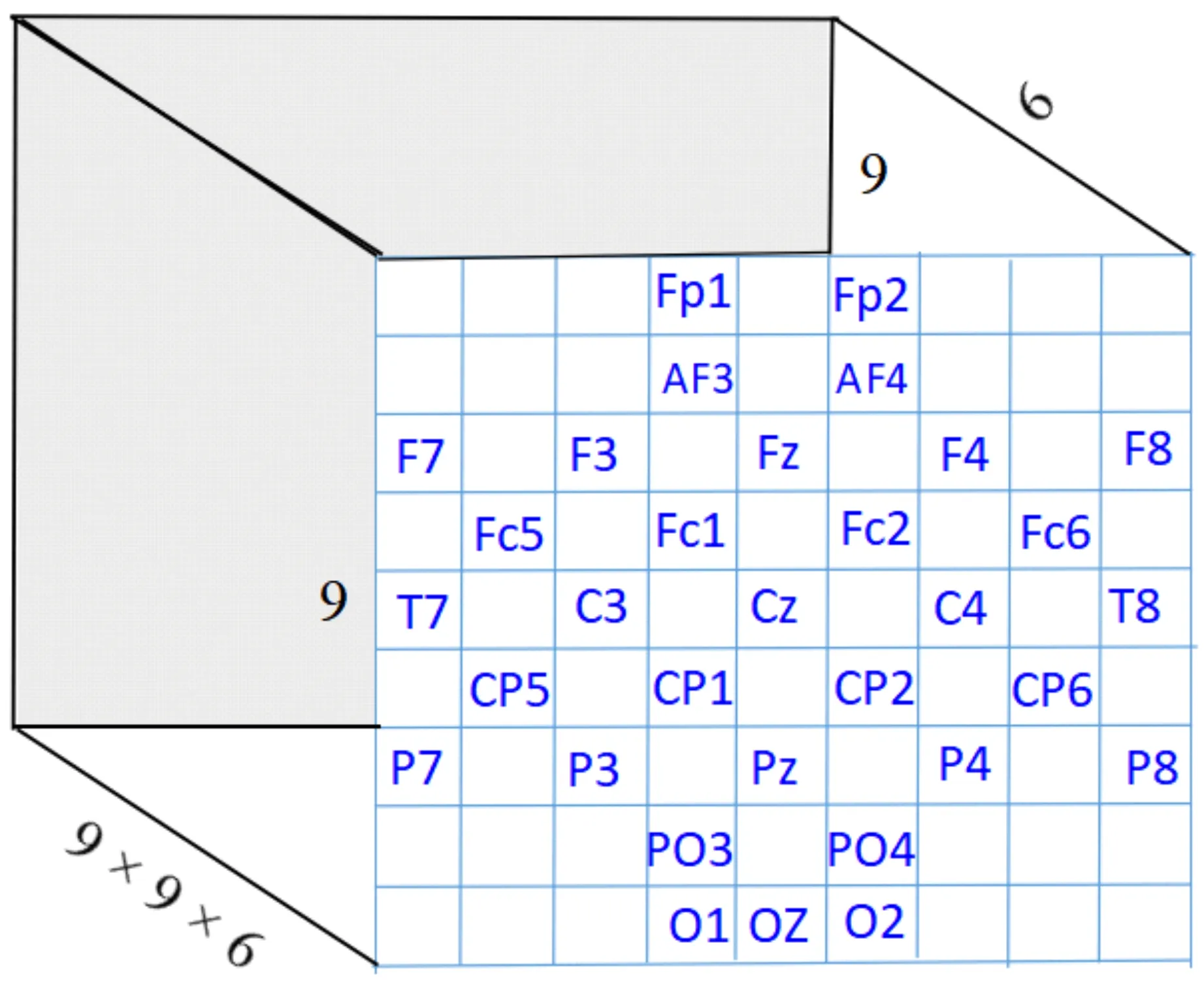
图2 3D矩阵特征结构图

1.3 多维卷积神经网络

在深度学习方法中，卷积神经网络CNN在图像相关任务中取得了突破[12]，逐渐被越来越多地应用于EEG的情绪识别当中.Lin等[13]在网络模型中首次引入了1×1的卷积核.Szegedy等[14]使用并行多尺度卷积滤波器学习输入图像的不同信息，以获得更好的深层图像表示.Liu等[15]提出了一种具有1×1卷积和多尺度卷积结构的CNN模型，用于时间序列分类.在上述工作的启发下，本文提出了多维卷积神经网络模型，即将单变量卷积与多元并行卷积相结合的CNN模型来对3D脑电特征进行情感识别.

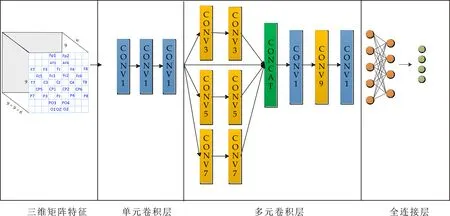
图3 多维卷积神经网络结构

本文使用的卷积神经网络将单元卷积与多元卷积相结合，并行提取深度特征并进行情感分类，下文统称该模型为MCNN.如图3所示，MCNN网络由四部分组成，分别为特征输入层、单元卷积层、多元并行卷积层、全连接层和输出层.该结构的特点在于将单元卷积与多元并行卷积相融合来同步提取更具判别性的EEG多元深层时空特征.

输入层：该层输入的数据为三维EEG特征矩阵，每个样本大小为9×9×特征数.

单元卷积层：该层使用了大小为1×1的卷积核来扫描每个通道以增强模型的局部抽象能力并加深网络.在每进行1×1卷积后，使用ReLU激活函数来获得非线性结果.

多元卷积层：该层分别采用3×3、5×5和7×7大小的卷积核来提取不同视野下的局部脑电特征.该卷积核的大小取决于输入层3D矩阵特征的表示形式.每个不同的卷积网络都包含两层，第一层将局部EEG通道分组在一起来学习通道间的局部相关性，第二层用来捕获组与组之间的上下文相关信息，每个卷积层上使用相同的填充，相同地，在每次卷积运算之后，使用ReLU激活函数获取非线性输出，接着将多元卷积的结果进行连接.该多元卷积层保留了每组卷积的独特功能，多层卷积级联之后，再进行一次卷积，该卷积核大小与输入数据的大小相同，最后滤波器以不同的方式将每个张量压缩成向量.

输出层：该层的输入是多元卷积层的输出，为了防止过拟合，在该层后加入Dropout层，然后接入SoftMax层进行分类.该模型的损失函数采用的是交叉熵函数：

(10)

式(10)中：q(i)是估计的分布，而p(i)是真实的分布，使用初始学习率为0.000 1的自适应矩估计优化损失函数.

与传统CNN不同，所提出的MCNN模型针对多通道脑电信号，考虑到了不同通道之间以及各个区域之间的相关性和交互作用，能更充分地挖掘3D脑电特征矩阵中与情感相关上下文语义特征，从而提高了情感识别的性能.

2 数据集及预处理

2.1 数据集

本文采用公开的大规模DEAP数据集[16]进行实验，以验证并评估所提方法的性能.该数据集记录了32个被试观看40个时长约为1分钟的、带有不同情感倾向的音乐视频所诱发的脑电、心电、肌电等生理信号，每位被试者对每次视频在唤醒度、效价、喜好，优势度和熟悉度方面使用1～9的连续数值进行评价.取DEAP数据集中用BioSemi系统采集的每个被试32通道63秒的EEG信号作为研究对象，其电极按照10～20系统定位[17]，采样频率降至128 Hz，为了消除直流噪声、电源噪声和其他伪迹，使用4～45 Hz的带通滤波器进行数据过滤，再采用盲源分离技术去除了眼电干扰.

2.2 脑电信号预处理与特征提取

本实验中，原始EEG信号表示为32(subs)×40(trials)×40(channel)×8 064(samples)，其中8 064表示128(samples)×63(s)，标签Labels表示为40(trials)×4.对该原始数据进行预处理，从40个通道中提取所需的32个EEG通道的数据，由于人类视觉上的延迟反应，本文将前3秒作为基准，提取后60秒的EEG信号作为实验数据，预处理后的数据表示为32(subs)×40(trials)×32(channels)×7 680(samples).标签选取效价和唤醒度两个维度，即40(trials)×2.

本文作者之前的实验发现[3]，使用大于或小于1秒的窗长进行分段都会降低分类的性能，这也许与人类大脑情感活动的周期长度有关.因此，本文仍采用1 s时长对EEG序列进行不重叠分段，即样本划分，每次试验得到60个片段，每个片段包含128个采样点，每个采样点包含32个通道，即每个被试的EEG数据可表示为40×128×60×32，对其进行维度变换，得到2 400×32×128的脑电数据，每个被试共有2 400个EEG片段，每个片段大小为32×128.对标签进行相同维度的转换，可表示为2 400×1.

接下来对该原始特征分别提取均值、方差、标准差、一阶差的绝对值的平均值、二阶差的绝对值的平均值、近似熵6种时域特征，然后按照第一章中的方法将32个通道的数据转换成二维网状结构，得到128×2 400×9×9的数据表示，6种特征进行拼接后得到三维时域矩阵特征(3D_Time-domain_matrix features)，其维度为307 200×9×9×6，即输入深度模型的样本数为307 200，对应标签为307 200×1.

神经科学和心理学的研究表明，EEG信号在delta(1 Hz～4 Hz)，theta(4 Hz～8 Hz)，alpha (8 Hz～13 Hz)，beta(13 Hz～30 Hz)和gamma(30 Hz以上) 5个频段上包含大量与情绪等心理活动密切相关的节律信息[18].从本文作者发表的文献[3]可知，EEG信号在4～45 Hz频带上的功率谱密度(power spectral density,PSD)特征在2D-CNN网络上的分类性能明显优于时域上的特征，这也许是因为PSD频域特征的提取需要在较大连续采样周期内进行，而情感脑电任务也是一种相对长时的大脑活动，所以频域特征能够捕获更多情感相关的大脑动态.因此，本文在原始特征的基础上，在4～45 Hz频带上利用快速傅立叶算法在1 s的EEG片段的每个通道上使用0.5 s的汉明窗无重叠地滑动提取64个PSD特征，每个被试40次试验共提取PSD特征的维度是2 400×32×64，然后采用跟时域相同的方法进行维度的转换，将5个频带及全频带频域特征进行连接，得到三维频域特征(3D_Freq-domain_matrix features)，其维度为153 600×9×9×6，标签也随之进行一致性转化，其维度为153 600×1.转换以后EEG样本包含了丰富的空间、时间与频域上的信息.

为了验证3D时域与频域融合特征的分类效果，本文将时域和频域特征进行组合，形成3D融合矩阵特征.为了降低计算复杂度，与频域特征的数据格式保持统一，将6种时域特征降采样至64，采用相同的样本划分方法，则3D融合特征维度为307 200×9×9×12，标签做同维度转换，即得到3D时频域融合特征的样本数据.

接下来处理每个EEG样本的标签，基于被试对每个视频在1～9范围内的评价值以中位数5作为阈值将效价和唤醒度上的评价值划分为两类，在某个维度上解决2分类问题时，大于5代表高类或正性指标，用1表示；小于或等于5代表低类或负性指标，用0表示.

3 实验及结果分析

本文使用了DEAP 数据集中32名被试的脑电数据来训练和验证该方法的性能及泛化能力.所提模型是在基于tensorflow1.13，GeForce GTX 1080 GPU上实现的.实验采用十折被试交叉验证技术来评估所提方法在DEAP数据集中脑电信号的效价和唤醒度两种维度下的两类情感分类性能.具体而言，从32个被试中，每次提取四个被试的数据做测试集，其余随机再取4个被试的数据做验证集，剩余数据做训练集.重复上述过程十次，直到测试完所有被试数据.Bach_size大小设置为80，迭代轮数Epochs设置为200.本文选取情感分类的准确率作为评价所提出方法性能的指标，最终分类准确率取10次实验所得准确率的平均值.

为进行比较，本文还使用如下特征和目前较先进的模型作为基准方法在相同数据集上进行相同条件下的EEG情感分类实验，对比方法如下：

3种脑电特征：样本熵特征(Sample Entropy)[19]，改进的微分熵特征(MD-DE)[20]，二维网状特征(2D-mesh-matrix)[21]；

4种深度学习方法：深度LSTM递归神经网络[22]，二维卷积神经网络(2D-CNN)[23]，基于注意力机制的分层双向GRU网络(H-ATT-BGRU)[24]，级联卷积递归神经网络(Casc-CNN-LSTM)[21].

3.1 不同三维矩阵特征的分类性能对比

首先，为了验证3D频域矩阵特征的优势，将3D时域矩阵特征、3D频域矩阵特征和3D时频融合矩阵特征分别输入MCNN模型进行效价和唤醒度两个维度下的情感二分类实验.MCNN模型的结构和参数配置如本文1.3所述，实验结果如表1所示.

表1 不同三维矩阵特征在MCNN模型下的分类准确率

从表1可以看出，基于频域3D矩阵特征与多维卷积网络(MCNN)的情感识别准确率在唤醒度和效价上分别高达85.88%和87.32%，均高于时域矩阵特征和时频融合矩阵特征，验证了本文情感识别方法的有效性.在唤醒度上，与融合特征和时域特征相比，频域特征上识别准确率分别提高了4.36%和1.05%，在效价上，频域特征上识别准确率分别提高了5.36%和2.13%.可见，频域特征能够有效捕获更多情感相关的大脑动态，PSD特征相较于时域特征在情感分类任务中的准确率更高.

3D时频域融合特征也获得了较好的结果，但还是略低于3D频域矩阵特征和3D时域矩阵特征，原因可能是融合特征包含的信息太多，出现特征数据冗余，使有效特征不够显著，但是频域与时域的融合特征也在一定程度上扩充了数据量并提升了模型的泛化能力.

由于在效价维度下实验结果更好，本文选取效价维度下MCNN模型训练图进行对比分析，其中蓝线表示平均误差loss，红线表示模型训练准确率acc.

图4为效价维度下3D时域特征的训练过程曲线.由图4可知，随着迭代轮数iteration的增加，平均误差loss虽然出现几次骤然上升又急速下降的情况，但整体依然呈现不断向0趋近的态势，训练准确率acc整体向1趋近并最终收敛.

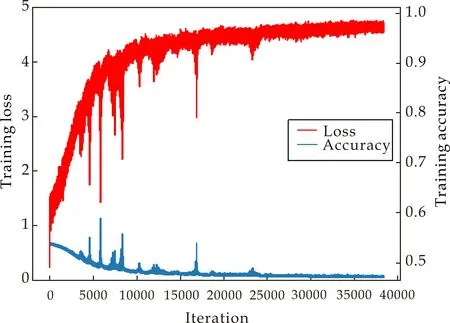
图4 效价维度下3D时域特征的模型训练图

效价维度下3D频域特征的训练过程曲线如图5所示.由图5可知，整个过程经过了20 000多次迭代，平均训练误差loss呈下降趋势.与此同时，训练准确率acc以同样的趋势螺旋上升，直至训练准确率趋近于1.loss在不断收敛的同时，并在不间断的进行震荡，在loss开始进行大幅度震荡时，acc也同频率的大幅度变化，这一现象可能是由于在参数训练过程中，梯度陷入了局部最优解.经过几次大幅度的震荡后，随着训练数据的更新，Adam优化器不断将参数经过偏置矫正，最终训练误差曲线以螺旋下降的方式下降至0收敛，准确率以同样的趋势螺旋上升向1靠近，直至拟合完成.

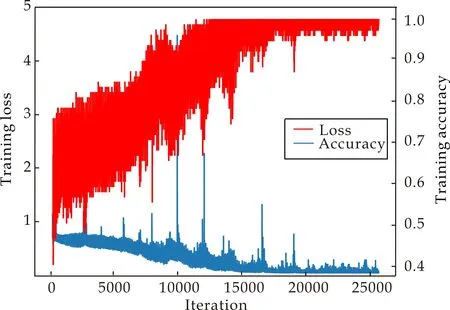
图5 效价维度下3D频域特征的模型训练图

3.2 三维矩阵特征与其他基准特征的性能对比

为了对比所提3D频域矩阵特征的性能，本文选择了3种目前用于情感识别性能较好的手工脑电特征在MCNN模型下进行对比实验，实验结果如表2所示.

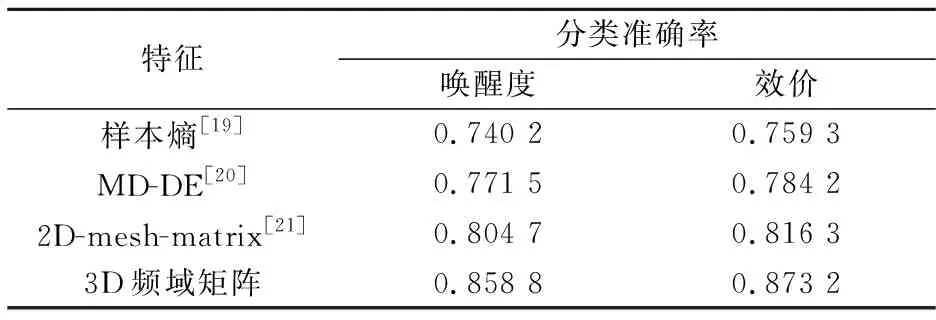
表2 基准特征在MCNN模型下的分类准确率对比

从表2可以看出，频域3D矩阵特征比改进微分熵特征(MD-DE)在唤醒度和效价上的分类准确率分别提高了8.73%和8.86%，比本文作者之前提出的二维网状特征的识别准确率提高了5.41%和5.69%.该结果很大程度上归因于所提3D频域矩阵特征不仅捕获了不同脑电通道间的空间信息，还将多个频带PSD特征进行级联，能够更直接准确地反应大脑皮层EEG信号的空间相关性和时频动态，表明3D频域特征矩阵可以有效提高多通道EEG情感识别的性能.

3.3 三维矩阵特征与二维特征的对比

为了验证三维特征的优势，本文还使用所提的MCNN模型对二维的时域和频域特征进行情感分类对比实验.32通道的时域特征可以构造32(channels)×6的2D特征矩阵.根据2D特征矩阵的大小，将多变量卷积层的滤波器大小分别设置为2×2、3×3和5×5，将级联后的第二个卷积层的卷积核大小设置为32×6，Bach_size大小和迭代轮数也分别设置为80和200.

两种特征的识别结果如表3所示.在时域上，与2D特征对比，3D矩阵特征在唤醒度和效价上的识别准确率分别提高了12.38%和 11.5%；在频域上，与2D特征相比，3D矩阵特征在唤醒度和效价上的识别准确率提高了7.17%和 8.26%.使用二维特征也获得了相对较好的结果，恰好验证了所提多维卷积神经网络的有效性.对比二维特征，三维矩阵特征中的增益信息可以更加明显地提高情感识别准确率.此外，3D时域矩阵比2D频域矩阵的识别准确率平均高出了6.1%，证明了3D脑电特征表征方法的优势.

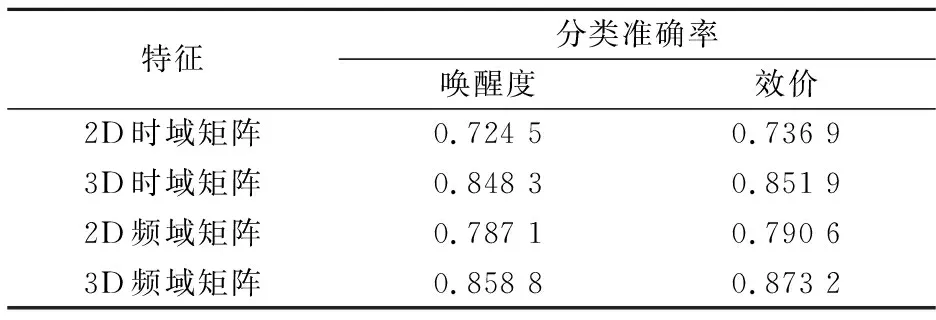
表3 三维矩阵特征与二维特征在MCNN模型下分类准确率对比

3.4 3种MCNN变种模型的性能比较

为了证明所提出MCNN模型结构的优势，本文做了3种MCNN模型的变种，分别称为模型MCNN-1、MCNN-2和MCNN-3.其中，MCNN-1在单变量卷积层中使用3×3卷积滤波器，而不是使用1×1卷积滤波器，用于验证MCNN中 1×1卷积层的优势.MCNN-2仅在多变量卷积层中使用带有5×5滤波器的单向卷积，用于验证MCNN中多元卷积层的优点.MCNN-3同时在单变量卷积层中使用3×3卷积滤波器，在多变量卷积层中仅用5×5滤波器的单向卷积，来验证MCNN上述两个结构的优点.三个变种模型中的其他参数保持不变，10折交叉验证集也都保持不变.为了公平起见，将迭代轮数epoch和批量大小Bach_size分别设置为200和80.表4展示了效价和唤醒度两个维度下3D特征矩阵特征在MCNN不同结构变种模型上两类情感分类结果.

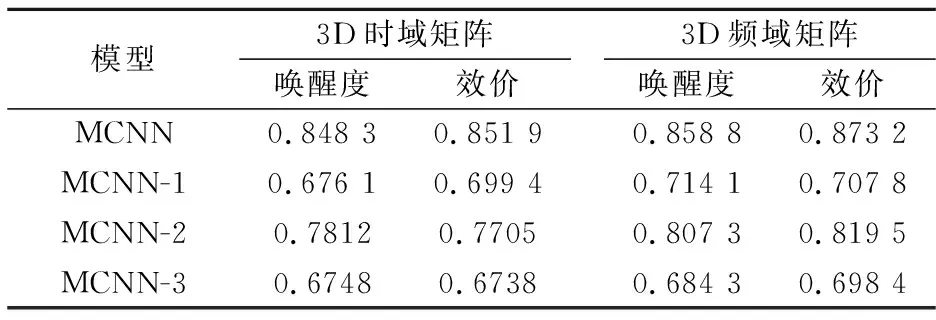
表4 3D矩阵特征在不同MCNN变种模型下分类性能对比

由表4可知，与MCNN-1、MCNN-2和MCNN-3相比，MCNN在唤醒度上3D时域特征上的识别精度分别提高了17.22%、6.71%和17.35%，在3D频域特征上的识别精度分别提高了14.47%、5.15%和17.45%；在效价维度上，MCNN在3D时域特征上的识别准确率分别提高了15.25%、8.14%和17.81%，在3D频域特征上的识别准确率分别提高了16.54%、5.37%和17.48%.实验结果表明，所提出的MCNN的性能远优于MCNN-1和MCNN-3.这证明了所提出的多维卷积模型MCNN在结构上的优越性.从MCNN-1和MCNN-2的结果可以看出，单变量卷积层对分类性能的影响比多变量卷积层的影响更明显，原因是每个通道的时域和频域特征提供了与情绪状态密切相关的信息.这也表明，脑电通道之间的空间相关性以及区域之间的相关性可以有效提升情感识别的性能.

3.5 所提MCNN模型与其他较优模型的性能比较

为了进行比较，本文使用了4种基准模型在相同的数据集上针对3D频域矩阵特征进行脑电情感分类实验，对比结果如表5所示.由表5可以看出，所提MCNN模型达到了更优的性能，比目前最优的Casc-CNN-LSTM级联卷积神经网络模型的分类准确率在唤醒度和效价上分别高出3.52%和4.18%.究其原因可能是由于改进后的MCNN卷积神经网络更加复杂，利用单元卷积增加了局部抽象能力，在多元卷积层中使用了双层多维度级联操作，使模型不仅能够提取不同通道间的空间信息，还利用了不同区域之间的交互信息，联合提取到了更具鉴别力的情感特征，从而获得更多与情感相关的增益信息，提升了模型的性能.因此，根据具体的脑电特征表示形式构建相应结构的深度学习模型是获得可区分特征和更高情感识别性能的关键.

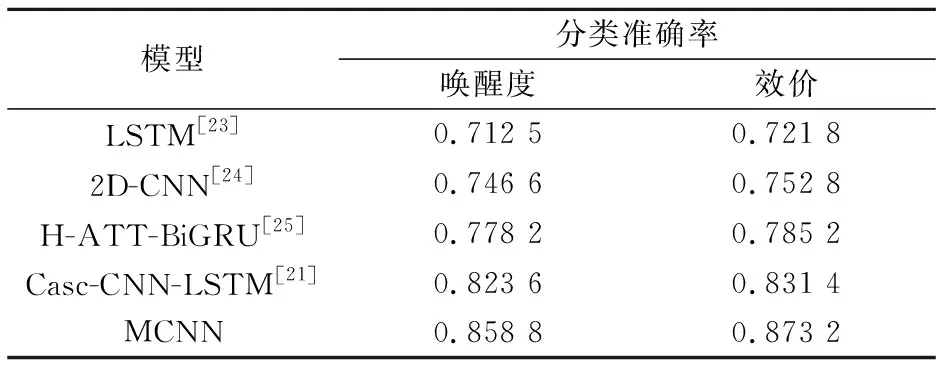
表5 多维卷积模型与其他深度模型性能对比

3.6 MCNN与多种机器学习算法融合分类比较

MCNN模型能够从3D特征矩阵中提取每个EEG通道的深层特征以及通道之间的相关特征.为了进一步证明该方法的有效性及泛化能力，将MCNN提取的高级特征输入到经典机器学习算法中进行对比分析.将每个样本的3D频域特征矩阵都输入到训练好的MCNN模型中，然后将完全连接层的最后一层中512个神经元的输出作为学习到的高级语义特征，送入常用经典的机器学习算法进行情感分类.这些算法包括带线性核的支持向量机(SVM-linear)、决策树(DT)、随机决策森林(RDF)、K近邻(KNN，neighbors=5).所用的10折交叉验证集在这里保持不变.

表6显示了使用高级语义特征的经典机器学习算法的分类性能.实验结果表明，SVM-linear分类效果最好，在唤醒维度上的最高平均识别准确率为96.35%，在效价上的最高平均识别准确率为96.74%，其他分类算法也获得了令人满意的效果.与使用SoftMax进行分类相比，利用MCNN进行高级特征学习和经典的机器学习算法进行分类可以显著提高情感识别的性能.再次表明，充分利用每个EEG通道的深层语义特征以及通道之间的相关信息可以显著提高情感识别的性能，本文所提MCNN模型能够有效地从三维脑电特征表示中学习这些显著特征.

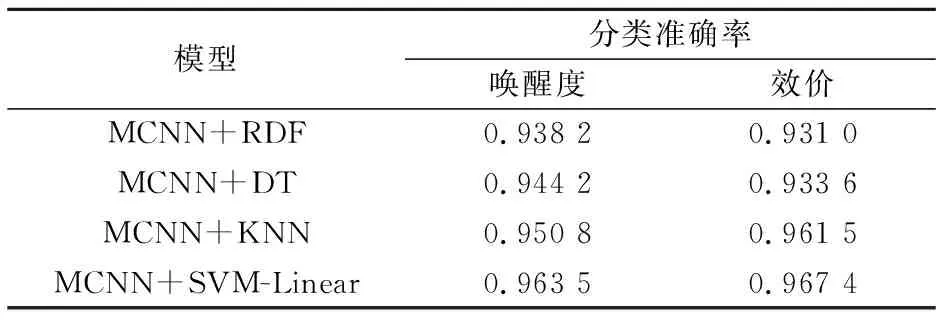
表6 MCNN与机器学习算法融合的分类性能对比

4 结论

情感在人类生活中起到至关重要的作用，近年来，人工智能领域越来越看重对情感识别的研究.本文利用三维矩阵表示了带有时频域增益信息的时空脑电特征，又利用多维卷积网络增强模型的局部特征抽象能力，学习脑电图大区域的对称属性和小区域的特殊属性，提取了更具判别性的深层脑电特征并进行情感分类，较大地提升了独立于被试的两类情感识别准确率.

本文采用了多方对比实验来验证所提方法的有效性.为了验证3D频域矩阵的有效性，分别与2D特征、时域特征、时频融合特征以及其他较先进的手工特征进行了对比；为了验证MCNN模型的性能，构建了多个MCNN变种模型，并且同目前较先进的深度模型进行横向对比；为了验证MCNN模型的泛化能力，将该模型学习到的高级特征与经典机器学习算法进行融合比对，融合后的复杂模型在分类准确率上都有较大的提升，验证了所提方法的可行性和可靠性.后续我们将对该方法进行更深层的改进，结合迁移学习的方法开展跨领域独立于被试的EEG情感分类研究，进一步提高基于EEG的情感识别的性能.