基于μ律爆炸算子和信息交流映射策略的烟花改进算法
滕志军, 李 哲, 王幸幸, 皇甫泽南, 申博冉
(1.东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室, 吉林 吉林 132012; 2.东北电力大学 电气工程学院, 吉林 吉林 132012; 3.吉林大学 数学学院, 吉林 长春 130022)
0 引言
近年来,针对复杂的优化问题,群智能算法凭借其简单、灵活、寻优速度快的优点成为解决这类问题的强有力工具[1].目前,群智能算法有粒子群算法[2,3]、遗传算法[4]、灰狼算法[5]、萤火虫算法[6]、烟花算法[7]等.烟花算法(Fireworks algorithm,缩写为FWA)由北大教授谭营于2010年受烟花在夜空中爆炸产生火花的自然现象启发而提出,其优越的特性受到不同领域科研工作者的关注,对FWA进行改进提高算法性能也成为了研究的主要方向.
针对原始烟花算法的不足和缺陷,Gong等[8]提出了具有自适应参数的动态搜索烟花算法(dynFWA),通过引入自适应系数调整爆炸半径放缩系数和新的选择策略加快算法收敛,增强了算法的求解性能.Zhao等[9]提出了一种核心烟花信息引导的自适应烟花算法(AFWA),该算法通过CF烟花位置信息来扩展最佳烟花的爆炸幅度和更新方向,在该方向上产生更多的爆炸火花来增强搜索能力,加快算法收敛.Zheng等[10]提出了一种增强型烟花算法(EFWA)通过通过引入新的最小半径幅度检查策略和精英选择策略,减少了算法运行时间.Krouska A等[11]在增强型烟花算法(EFWA)的基础上对最小半径策略进行修改提出新的爆炸方案,引入信息交换策略,平衡了烟花算法的局部与全局搜索能力.Luo等[12]将混沌映射策略与自适应烟花算法相结合,保证了烟花算法局部搜索的精度,满足了全局搜索的多样性.
此外,Yu等[13]受各种爆炸方式和形状的启发提出了基于多层爆炸策略的烟花算法,使用目标函数来评估前一层爆炸产生的火花个体以此来确定下一层的爆炸形状和火花分配,提高了爆炸性能.Cheng等[14]提出一种混合混沌机制与levy变异的改进烟花算法,利用混沌机制使初始种群分布均匀,引入levy变异算子增强烟花的全局搜索能力.朱启兵等[15]结合引力搜索算法的思想提出了一种带有引力搜索算子的烟花算法,增强了优质火花与其它火花之间的信息交互,增加了烟花种群的多样性,提高了算法寻优性能.Yue等[16]通过引入自适应平衡系数将灰狼算法的全局寻优与烟花算法强大的局部搜索相结合提出对多维复杂空间进行优化.Zhang等[17]提出了蜂群-烟花混合算法来求解多目标优化问题,首先使用蜂群算法(ABC)进行全局搜索,当寻找到更好蜜源时,引入动态烟花算法(dynFWA)快速执行局部搜索增强算法的性能.
为进一步提升烟花算法后期的寻优速度、平衡局部和全局的寻优能力,本文提出一种基于μ律爆炸算子和信息交流映射策略的烟花算法(Firework algorithm based onμ-law explosion operator and information exchange mapping strategy,缩写为μFWA).该算法采用适应度等级代替适应度并将非均匀量化的μ率特性曲线函数作为一个转移函数构建新的烟花爆炸公式,改善了后期最优烟花与其它烟花差异不明显造成的收敛速度减慢的问题.引入缩放因子动态调整变异范围和随着迭代次数动态调整μ率特性曲线的形状参数μ值,均衡局部和全局的搜索能力.最后提出了基于信息交流的映射策略,充分考虑了超出边界火花的位置信息,更有针对性的对超出边界的火花进行映射.
1 烟花算法简介
1.1 爆炸算子
爆炸算子是烟花算法核心,烟花爆炸时根据适应度值自适应的控制爆炸的范围和爆炸火花数目,爆炸强度公式如下:
(1)
式(1)中:Si表示第i个烟花产生的爆炸火花数目,M是火花总数目,f(Xi)表示当前烟花Xi的适应度值,Ymax表示当前种群中适应度值最差的个体的适应度值,ε是极小数.
(2)
式(2)中:Si表示第i个烟花产生的火花数;a,b为常数;round()表示四舍五入取整.保证通过爆炸算子计算得到爆炸火花数目为整数.
(3)
式(3)中:Ai表示第i个烟花的爆炸范围;A是烟花爆炸总幅度;f(Xi)表示当前烟花Xi的适应度值;Ymin表示当前种群中适应度值最优个体的适应度值;ε是极小数.
1.2 变异算子
(4)
g=N(1,1)
(5)
式(5)中:g是服从均值为1方差为1的高斯变异.
1.3 映射策略
烟花算法在执行爆炸时,难以避免会产生超出边界区域之外的火花,然而这些火花会降低算法的寻优能力,因此采用映射策略将经爆炸导致的越界火花重新映射回可行域内.
(6)
1.4 选择策略
FWA采用基于距离的轮盘赌选择策略,公式如下:
(7)
式(7)中:‖xl-xj‖ 表示火花xl,xj之间的欧氏距离;R(xl)为第l个火花到所有火花的距离.
(8)
式(8)中:p(xl)为爆炸火花xl被选择为下一代烟花的概率,由式(8)知,据其它爆炸火花距离更远的火花更容易成为下一代烟花,保证了种群的多样性.
2 改进烟花算法
2.1 新的爆炸算子
烟花算法的爆炸算子产生的爆炸火花数目在不同的情况下是不稳定的.适应度值随着目标函数的不同和搜索空间中位置的不同而剧烈波动.爆炸火花的数量没有规律,相应地,最佳烟花产生的爆炸火花的数量无法控制.最佳烟花的适应度如果很小时,可能会占用几乎所有资源,相反劣质烟花爆炸产生的火花数目会很少,导致算法易陷入局部最优.当算法进入迭代后期时,由于所有烟花都集中在最优值附近进行探索,各个烟花的适应度值差别不大导致最优烟花分配的爆炸火花数目和爆炸范围与其它普通烟花区别很小,体现不出最优烟花优势,使算法在后期收敛速度减缓.因此,本文用适应度等级代替适应度值来计算烟花的爆炸火花数目和爆炸幅度,引入非均匀量化的μ率特性曲线函数作为传递函数Ta(n)将烟花序号映射为函数值构建新的烟花强度算子.适应度值转化适应度等级量化值的传递函数Ta(n)计算如下:
(9)
式(9)中:n是烟花序号,μ是传递函数形状的参数.由图1知,传递函数随着μ的减小会变得更加均匀.μ随迭代次数的改变能动态的调整烟花爆炸火花的数目和幅度,且随着迭代次数增加而减小,适应度较差的烟花随着迭代次数的增加火花越来越少,爆炸半径越来越大,适应度较优的烟花随着迭代次数的增加火花越来越多,爆炸半径越来越小.让全局搜索在早期完成,加强算法后期的局部搜索,更好的平衡了算法的局部和全局寻优能力.
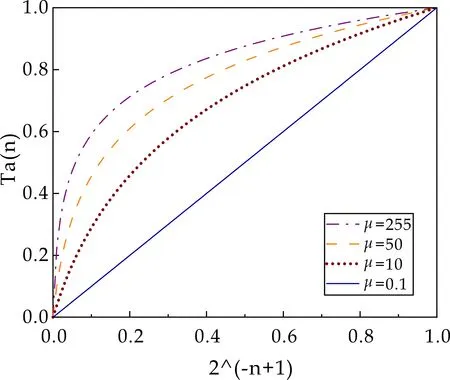
图1 μ率曲线
爆炸火花数目和范围计算公式如下:
(10)
(11)
式(10)、(11)中:N是烟花总数,n是烟花序号,Sn是适应度排名为n的烟花的爆炸火花数目,An是适应度排名为n的烟花的爆炸范围.基于μ律爆炸算子的伪代码如下:
2.2 改进的变异算子
烟花算法中的变异算子可以增强种群的多样性,使算法跳出局部最优而找到全局最优解.但传统烟花算法采用的高斯变异对于原点附近的变异火花很难通过变异跳出原点附近的位置,随机变异又缺乏与最优火花个体之间的信息交流,因此本文提出一种新的变异策略,引入缩放因子来动态的控制变异范围,算法前期增大变异范围,增加了找到最优值的可能性,后期减小变异范围,与爆炸火花一起进行局部搜索,一定程度上提高了算法的收敛能力.改进变异算子的公式为:
(12)
(13)

Algorithm 2:变异火花产生方式Input:最优烟花位置xkbest,火花总数M,缩放因子F.Output:变异火花位置1.for l=1 to variationNum2.i=ceil(rand*M);k=round(rand*dim) //随机选择第k维第i个火花作为变异火花3.计算缩放因子F4.根据公式(12)产生变异火花5.if xki,b超出边界;Then6.根据映射策略将其映射到可行域内7. end if8.end for
2.3 基于信息交流的映射策略
烟花算法的映射策略主要是将利用爆炸算子和变异算子产生的超出可行域的火花映射回可行域内,保证种群的完整性.烟花算法的映射策略主要分为取余映射和随机映射,取余映射易将超出可行域的火花映射回原点附近,浪费大量的搜索机会,而提出的均匀随机映射虽然避免了取余映射的缺陷,但是忽略了生成火花的位置信息,具有较大的随机性.因此本文提出了一种基于信息交流的映射策略,首先通过c来决定进行局部映射还是全局映射.
(14)
c为一条前期骤减后期缓慢变化的曲线,保证算法局部和全局映射的平衡性.如果c≥0.5,利用式(15)将超出可行域的火花映射到爆炸烟花或者变异火花的附近.如果c<0.5,利用式(16)将超出可行域的火花映射到最优火花附近.
(15)
(16)
本文提出的映射规则既充分考虑了爆炸火花的位置信息,将其映射到爆炸烟花与边界的区间内,比随机映射增强了位置的针对性,在一定程度上保留了超出可行域火花的位置特征.同时通过一定概率的全局最优映射,加快了算法的搜索效率和收敛速度,比传统的取余映射增加了种群的多样性.基于信息交流生成爆炸火花的伪代码如下:

Algorithm 3:映射策略Input:最优烟花k维的位置信息xkbest,爆炸火花xki,烟花k维的位置信息xkm,当前迭代次数evaTimeOutput:映射后的火花在k维的位置xki,p '1.if xki>UB或xki 本文提出改进之后的烟花算法的具体实现步骤如下: Step1设置烟花种群的数目,维数.设置爆炸火花数目M和爆炸幅度A; Step2在搜索区间内初始化产生N个烟花,并计算每个烟花的适应度值; Step3根据适应度值对烟花进行排序,利用式(9)将烟花的序号值转换为函数值,然后根据式(10)、(11)分别计算每个烟花进行爆炸时产生的火花数目和爆炸幅度; Step4产生爆炸火花,将超出可行域的爆炸火花通过式(15)或式(16)映射回可行域内; Step5随机选取某个火花通过式(12)产生variationNum个变异火花,并将超出可行域的变异火花通过式(15)或式(16)映射回可行域内; Step6计算爆炸火花和变异火花的适应度值,然后通过精英选择策略选择N个烟花做为下一代烟花; Step7判断evaTime是否达到evaTmax值,如果达到则输出最优解和最佳适应度值,否则返回Step3继续执行. 为验证本文所提算法的有效性,本文选择12个国际通用的基准测试函数(基准测试函数的具体信息如表1所示,实验时测试函数维数设为20维)进行仿真实验,F1~F6为单峰测试函数,含有一个全局最优解,以测试算法的开发能力.F7~F12为多峰测试函数,其含有多个局部极值,测试算法的全局探索能力.通过与FWA、EFWA、dynFWA、AFWA等改进烟花算法进行对比来分析本文算法的性能.为了保证寻优结果的稳定性,五种算法在每个函数上独立运行30次. 表1 12个基准测试函数 通过MATLAB对上述的基准函数进行仿真对比,实验初始数据为烟花种群数目为5,爆炸火花数目为50,初始爆炸幅度为40,变异火花数目为5,迭代次数为105,形状参数μini=0.1,μfin=500. 3.2.1 寻优结果对比 由于基本烟花算法在爆炸过程中,爆炸火花数目和爆炸幅度仅由适应度值得到,导致后期最优烟花与普通烟花区别不明显,造成寻优速度减缓,所以本文将适应度值进行排序,引入非均匀量化中的μ率特性曲线将序号值映射为函数值,重新构建爆炸算子.通过表2数据可知,本文所提算法在12个测试函数上都能表现出比较优秀的性能,相对于其它4种算法,通过μFWA得到的平均适应度值在7个函数上获得领先,特别是在F1、F2、F4、F5优势更加明显,反映了μFWA收敛精度更高.此外,μFWA算法的标准差相较于其它4种算法更小,说明该算法的稳定性较好. 表2 本文算法与改进型烟花算法平均值、标准差比较 3.2.2 收敛曲线对比 为比较5种算法的求解性能,本文对5种算法在12个测试函数上的收敛曲线进行对比,其结果如图2和图3所示. 图2所示的是5种算法在单峰基准函数(F1-F6)的性能对比.可以看出,在搜索初期本文μFWA算法收敛速度略慢于其它对比算法,主要原因是本文采用适应度值等级替代适应度值进行爆炸火花数目和爆炸幅度的计算,随机产生的烟花差异性比较大,基于适应度值的爆炸算子性能优于基于适应度值等级的爆炸算子,随着算法运行一段时间后,各个烟花集中在较小范围进行寻优,基于适应度值等级的爆炸算子体现出了更大的优势,从而收敛速度明显优于其它算法. (a)F1 (b)F2 (c)F3 (d)F4 (e)F5 (f)F6图2 FWA、EFWA、dynFWA、AFWA和μFWA在单峰函数上的收敛曲线 (a)F7 (b)F8 (c)F9 (d)F10 (e)F11 (f)F12图3 FWA、EFWA、dynFWA、AFWA和μFWA在多峰函数上的收敛曲线 图3所示的是5种算法在多峰基准函数上的收敛曲线.μFWA算法通过动态改变传递函数μ的值,增强各等级烟花的差异性,使得各等级烟花的爆炸数目和幅度随迭代时间动态调整,优秀烟花小范围大量搜索,劣质烟花大范围少量搜索,更好的平衡了算法的局部开采和全局探索能力.从图3可以看出,本文所提算法出现停滞的次数和时间明显少于其它对比算法,反映了本文算法跳出局部最优的能力强,不易陷入局部最优,能够较快的找到全局最优解. 为了进一步提高算法的寻优性能,本文提出一种改进的烟花算法,将适应度值等级替代适应度值构建新的爆炸算子,通过动态调整传递函数μ值,更好的平衡了算法的局部及全局搜索能力.引入缩放因子F,在前期增强种群多样性,后期可加强算法的收敛能力.同时基于信息交流的映射策略,既考虑了最优火花的位置信息,又通过一定概率的全局映射,提升映射火花的多样性,提高了火花的搜索效率,进而提高了算法的收敛速度.为验证本文提出算法的有效性,对12个测试函数进行了仿真实验,结果表明,μFWA比其它对比算法能更快的搜索到全局最优解,且稳定性好.下一步将把本文算法应用于WSN节点部署优化问题以进一步验证算法的有效性.2.4 算法流程
3 仿真分析

3.1 实验参数设置
3.2 仿真分析

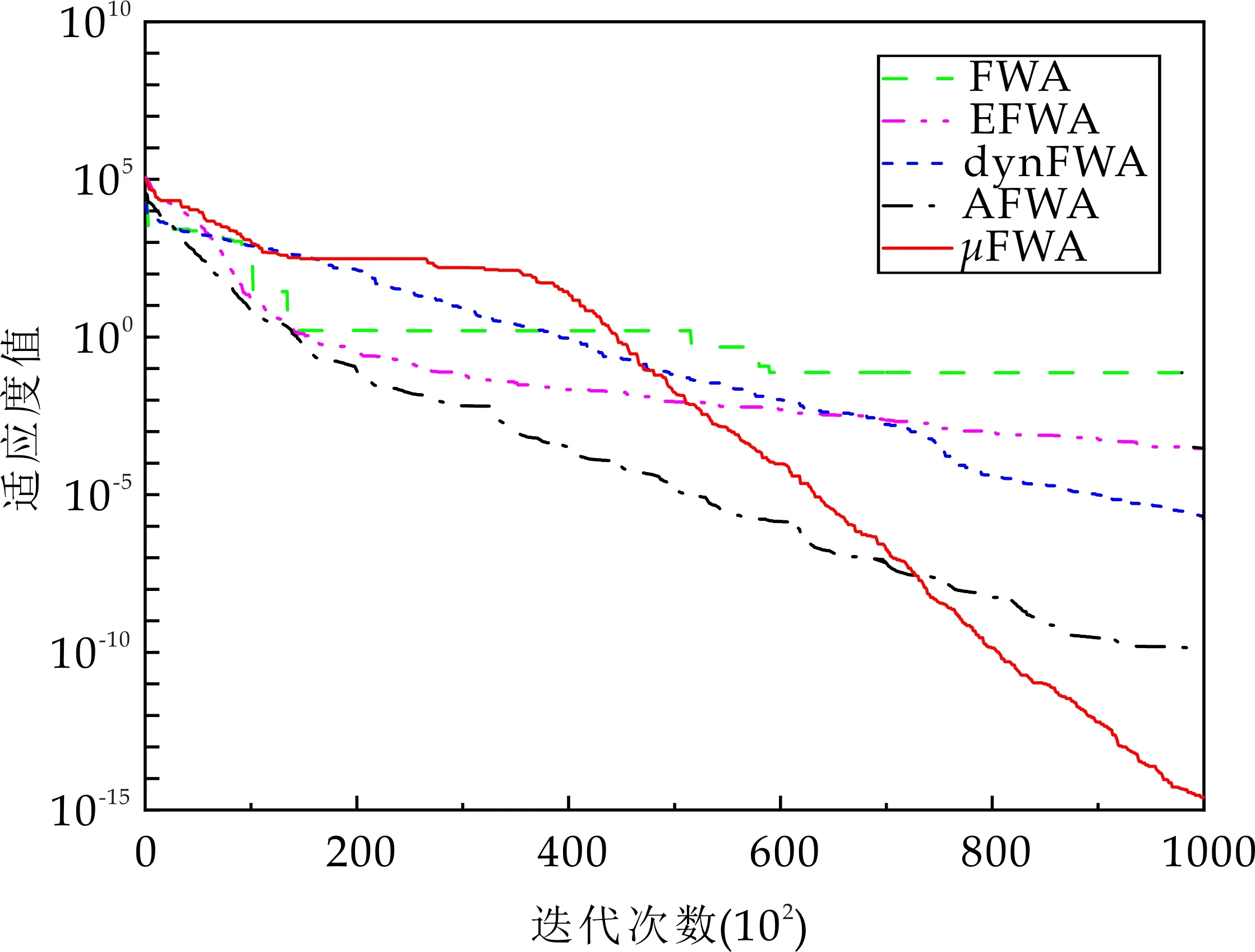
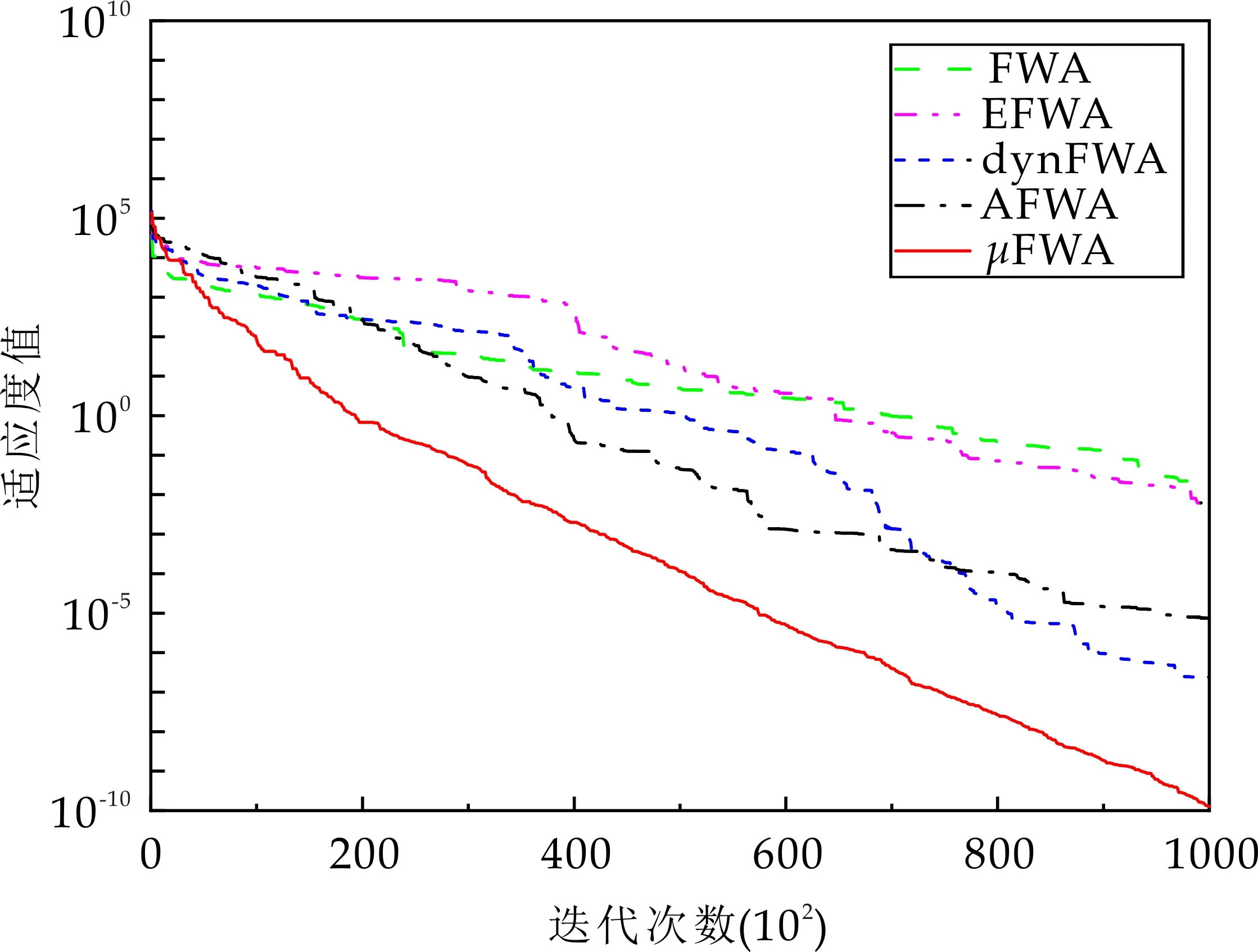
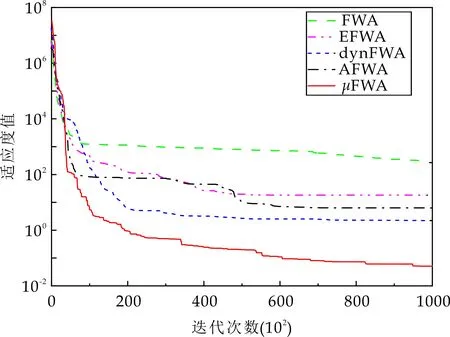


4 结论

