运用问题导学，提升初中数学课堂有效性

史艳飞

数学是义务教育阶段的基础学科，也是重要的学科，学生学好数学，对学生的思维的发展、综合素养的提升有很大帮助。随着新课改的推进，传统的应试教育的教学方法难以满足目前素质教育的新要求，不再适应学生的学习和发展，创新教学方法，构建学生积极探究、主动思考的互动课堂，让学生学得更多、收获更多成为新时期教师们的追求。问题导学法已经成为初中阶段优化课堂模式、提升教学有效性的可行之策。问题导学，就是课堂上以问题为导问、让学生积极参与课堂教学的教学方法。问题导学，有助于活跃课堂气氛、提高学生的思维力，让不同层次的学生在学习过程中思维、能力、素养等得到发展。下面，笔者将结合教学实践，对初中数学教学如何运用问题导学、提升教学有效性的问题进行简单论述。

一、创设问题情境，激发学生学习兴趣

兴趣是最好的老师。只有激发学生学习兴趣，才会让他们产生强烈的学习欲望，促进学生真正参与，主动探究，从而提升学习效果。数学教学中，应激发学生学习兴趣，结合教学内容实际，为学生创设问题情境，让情境成为学生学习的基础，促进学生从抽象的概念中认识和理解知识，感知学习内容，降低学习和理解的难度。在问题情境下教学，激发学生的好奇心和兴趣，提升学生自主学习能力。

如进行《图形的运动》的教学时，在课堂之初，笔者首先拿出剪纸，再逐渐展开剪好的简单图形，让学生看到展开后的一幅幅美丽的剪纸图案，再利用PPT为学生呈现杂乱无章的图片。如：

再点击“运动”，变成学生熟悉的奥运会的五连环标志图：

在情境创设的基础上，笔者提出问题：剪纸和五连环标志图漂亮吗？你能设计出这样精美的图案吗？这就是“图形的运动”的杰作。

此时笔者借助于肢体语言以及操作动作等，创设生动的情境：推拉可移动黑板、开关门窗等，让学生在观察的前提下，提出问题：老师刚才的动作中包含了哪些数学知识？引导学生回答出“平移”“旋转”等，从而引出：图形的平移和旋转，都属于“图形的运动”。这样的情境创设，基于学生的认知基础，基于学生的学习和生活，容易引发学生的经验，让学生感受到数学知识源于生活、运用于生活，激发学生探究学习的热情。同时，情境的创设，情境和即将所学的知识、情境问题的设计等有效融合，利于学生从情境中感知知识，从而激发学生主动探究的兴趣。

二、设计趣味问题，激发学生探究意识

趣味性的元素容易吸引学生的注意力，引发学生的兴趣。因此，问题导学教学时，问题的设计应富含趣味性，以趣味问题营建愉悦的学习氛围，让学生对数学学习产生主动探究的热情，激发学生积极思维的兴趣，从而提升学生学习效果。

趣味性问题的设计，应考虑学生的年龄特点、认知特点，还应注重问题中知识的联系，以保障问题的提出能立刻吸引学生的注意力，培养学生探究意识，真正发挥问题导学的作用。如《平面直角坐标系》的教学时，笔者首先设计开放性的问题，让学生“抢答”，以抢答游戏的开展活跃课堂氛围，让学生在活跃的课堂氛围中温故知新。如平面内确定一个物体的位置，需要几个数据？有哪些方法？这个问题虽然缺少趣味性，但是与游戏有机融合，则为问题增添了趣味性，激发学生积极思考、主动参与的欲望。学生给出不同的回答“用数对表示”、“（组，排）”“（排，座）”“（角度，距離）”“（经度，维度）”等等。笔者继续设疑，让学生抢答：（1）说出你在教室里的位置;（2）电影上有（6，3）你能解释（6，3）的含义吗？（3）你在大海中航行，但是大海中没有任何标志物，怎样才能确定你的位置？……这些具体的问题，激发学生积极去思考、主动交流，强化探究学习的意识，为有效课堂的构建埋下伏笔。

三、设计递进问题，促进学生对知识理解

问题教学法的主要作用是激发兴趣，引发学生的思考，促进学生探究学习。生活化、趣味性的问题设计，有助于学生学习兴趣的激发，探究学习主动性的调动。而递进问题导学，有助于学生学习方法的引导，是问题导学的又一行之有效的方法。教学中，教师可以根据教学内容，以知识逻辑推理为基础，将数学知识的概念、公式、公理、推论、思路、运用等，通过递进式的问题串，逐步引导学生的探究学习，以保证其自主学习效果。

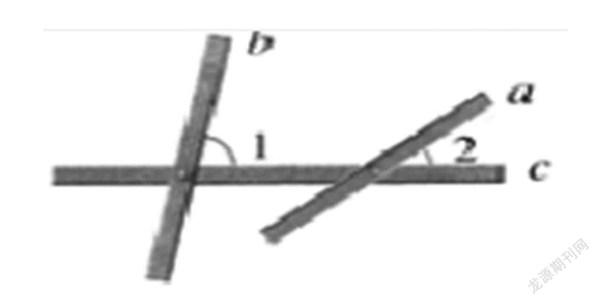
以《探索直线平行的条件》的教学为例，课堂之初，笔者创设生活情境：装修工人，向墙上钉木条，如果木条b与墙壁的边缘垂直，那么，木条a与墙壁的边缘夹角是多少度时，木条a和b平行？你能说出其中的道理吗？情境问题提出后，再呈现出情境图：

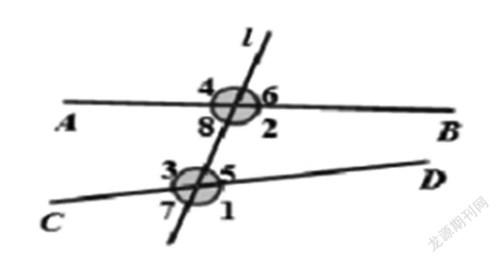
以增强问题的生动性、直观性。这个情境，基于学生的生活经验，让学生说说∠2等于多少度时，a与b平行。这是对经验的提问，容易引发学生的注意力和参与的兴趣。紧接着笔者借助于数学模型，引出“三线八角”的概念，引出同位角、内错角、同旁内角等的概念，然后给出图形再提出问题：你能找出几组同位角/内错角/同旁内角吗？

比一比，看看哪位同学找得多、找得全。这样的问题设计，是在感知了“三线八角”概念基础上的对这个知识的运用，以竞赛性的游戏，激发学生参与的主动性，营建乐学的氛围。再在此基础上，借助于数学模型木条b和c固定，转动a，然后，再提出问题串：

（1）观察、思考∠1和∠2的大小关系有几种？

（2）a和b的位置关系有几种？

（3）根据∠1和∠2的大小变化以及a和b的位置关系，你有哪些发现？

不言而喻，这些问题的设计，把学生从“三线八角”的认识和概念的感知中，逐渐引领到课堂教学的重点中。这个过程，是学生自主发现、主动探究的过程，有助于学生学习力、思维力、探究能力的提升和发展，优化了课堂模式，学生的学习方式也发生了巨大的变化。

四、设计生活问题，促使学生学以致用

数学教学的根本目的是让学生掌握知识，发展数学思想和方法的同时，提升运用能力，这也是新课标对数学教学提出的“学以致用”的新要求。落实这个目标和要求，需要教师根据教学内容，巧妙设计生活化问题，让学生将课堂所学运用到实际问题中以提升解决问题的能力，也拉近学生和数学的距离，让学生对数学的学习产生亲近感，产生学好数学有用的意识，从而强化数学学习意识。

如进行“认识三角形”的教学时，笔者提出问题：自行车的前后轮和车把、后座之间为什么设计为三角形？进行“菱形”的教学时，以学生们熟悉的马路上的“菱形”为切入点而设计问题：你们知道马路上的菱形的作用是什么吗？教学“圆”时，提出问题：自行车、电动车、小轿车等的轮子都是圆形的，为什么不设计为三角形、四边形、梯形？教学“勾股定理”时，设计测量旗杆的高度、墙面的垂直等问题……这些生活化问题的设计，丰富了学生生活经验，也促使学生运用所学知识解释生活中的数学现象，起到即学即用之效。

生活化问题的设计，旨在提升学生运用知识、解决实际问题的能力。这就需要教师找准生活和数学知识的切入点，在这个点上设计问题，强化学生的实践运用意识，提升学生灵活运用的能力。如进行“生活中的不等式”的教学时，笔者设计了诸如这类的问题：

（1）一次数学测验，老师只出了25道单选题，如果选对一道就得4分，全做对就得满分;而如果选错一个，就倒扣2分;如果全做错，就得50分。如果你想得分在60分以上，那么，你最起码得做对多少道题？

（2）《骆驼祥子》总共180页，2天读了50页。要在5天内读完这本書，那么，剩下的需要一天至少读多少页？

……

这类与学生学习生活密切相关的问题的设计，容易吸引学生思考和解决的兴趣，通过这类问题的思考和探究，进一步深化课堂所学的“不等式”的意义，引导学生在问题的思考和解决过程中学以致用，提升其分析问题、解决问题的能力。

五、设计层次问题，促进不同层次学生发展

有效课堂的主要标志是每一个学生在课堂上学有所获、有所得、能力得到提升和发展。而分层教学是两千多年前教育家孔子的教育理念，倡导“因材施教”，新课改也倡导“为了一切学生”“为了学生一切”的理念。教学中，教师应立足学生的层次性的实际，设计满足不同层次的学生学习的问题，促进不同层次的学生的学习和发展。

如《多边形内角和》的教学后，在练习环节，教师可以设计紧扣多边形内角和公式的练习形式，以强化每一个学生对公式的理解和运用。如：（1）你能算出6边形、7边形、8边形的内角和的度数吗？（2）在600°、720°、900°、1080°中，哪一个不可能是多边形的内角和？为什么？……这类练习，纯粹是多边形内角和的运用，难度系数较小，适合每一个层次的学生练习。而设计（1）如果一个多边形的每一个内角都是120°，那么这个多边形是（   ）边形;（2）小明在计算一个多边形的内角和时，计算结果是2220°，组长检查作业时，告诉小明，你少算了一个内角，这个这个少算的内角是（   ）°……这些练习的设计，较之于之前的几个，综合性、灵活性较强，满足优秀生的需求。层次性的问题，让不同层次的学生“跳一跳，够得到”，促进课堂有效性的落实。

总之，问题导学法，是培养学生核心素养的有效方法。导入时运用问题导学，可以点燃学生的热情;新授课中运用问题导学，有助于学生自主思考、勤于探究，深化学生对知识的理解和把握;新授后的问题导学，有助于学生解题准确率的提升，提升学生解题能力。教学中，教师应从素质教育的视角出发，有效运用问题导学，以让素质教育落到实处。