基于逐步回归分析法的表面粗糙度预测

张家有， 宋万万， 白玉珍， 韩 冰， 李路杰， 朱慧宁

(1. 辽宁科技大学 机械工程与自动化学院， 辽宁 鞍山 114051) (2. 沈阳飞机工业(集团)有限公司， 沈阳 110034)

轴类零件是精密设备不可或缺的组成部分，其表面质量对精密设备的工作状态有很大影响。磁粒研磨法作为一种精密加工的方法能够有效降低零件的表面粗糙度，提高其表面质量。一般来讲，零件的表面越粗糙，则摩擦阻力越大，磨损也就越快；但是，当零件结合表面过于光滑时，由于润滑油被挤出及分子间的吸附作用，摩擦系数反而增大，从而会加剧磨损[1]。因此,对工件表面粗糙度值的控制尤为重要。

在20世纪90年代，金东燮等[2]对旋转体圆柱形工件表面进行表面磁粒研磨加工，将表面粗糙度从2.5 μm降至0.2 μm。在加工微型阶梯轴时，陈燕等[3]使用匹配工件形状的磁极对磁极材料进行加工，在工件各处的磁场强度保持一致的基础上，达到均匀加工的目的。针对非磁性外圆表面的磁性加工中存在的部分磁性磨料分布在加工间隙外的现象，赵文渊等[4]将黏结法磨料改进为黏弹性磨料，使参与加工的白刚玉数目增多，加工能力增强。轴类零件的常用材料是碳素钢、合金钢、铸铁等导磁材料。对导磁材料进行磁粒研磨加工时，不再采用简单的磁极吸附磨料形成磨粒刷对试件进行研磨的方法，而是和工件形成一个新的磁场平衡状态，处于这种状态下的高速旋转的试件会带走部分磨料和研磨液，降低其研磨效率。

针对该问题，在加工时，将试件浸没在外壁镶嵌多个磁极的磨料容器中，防止磨料和研磨液的流失；且容器周围每个磁极都会形成1个磨料刷，增加了试件表面与磁性磨料的接触时间，不过也相应降低了一些磨料的流动性，降低了磨料的更新作用。在此加工方法下，为探究磁粒研磨工艺参数对轴类零件表面粗糙度的影响，利用逐步回归分析方法建立表面粗糙度预测数学模型，并通过试验验证预测结果的准确性。

1 试验及方法

1.1试验装置

试验采用超声波清洗加工后的试件，采用JB-8E触针式粗糙度测量仪检测表面粗糙度，采用VHX-500F超景深3D电子显微镜观察表面形貌。

图1为组合磁极磨料容器。磁性磨粒在磁场的作用下形成柔性磨粒刷，磁性粒子中的研磨相对工件表面进行划擦、切削、挤压，以达到对工件表面进行微量材料去除的目的[5-6]。圆形轴向磁极按圆周阵列排布，形成了变化更强的磁场梯度，可促进磨料的翻滚更新作用，提高其对工件的加工效率。

图1 组合磁极容器

采用普通铣床改造的试验平台，包括主轴、工件、夹具、组合磁极容器，试验装置如图2所示。所用磨料由烧结法制备的磁性磨粒和水基研磨液按一定质量比混合而成。试件为20CrMnTi材质制成的轴类零件(直径为15 mm)。磁性磨粒是将铁、白刚玉、黏结剂均匀混合后，经过压坯、烧结、破碎等步骤，制成具有研磨作用的细小颗粒(粒径为125 μm)，图3为磁性磨粒的微观形貌图，铁为基体，白刚玉为研磨相。水基研磨液为劳力恩SR-9911水基研磨液。加工时，将磁性磨粒与研磨液按照一定质量比混合均匀注入磨料容器中，之后工件在主轴驱动下进行旋转运动。工件表面与磨料刷之间存在相对运动，使得磨料刷不断地对工件表面进行微量的材料去除，达到光整加工的目的。

图2 试验装置

图3 磁性磨粒微观SEM图

1.2 试验方案

为明确不同的工艺参数与工件表面粗糙度之间的定量关系，以加工时间、工件转速、磁性磨粒和研磨液的质量比(m1/m2)、磨粒粒径为自变量，以工件表面粗糙度作为因变量设计试验，因素水平分配如表1所示，对试验结果以及不同的工艺参数进行逐步归回分析，建立数学模型，并对其准确性进行验证。

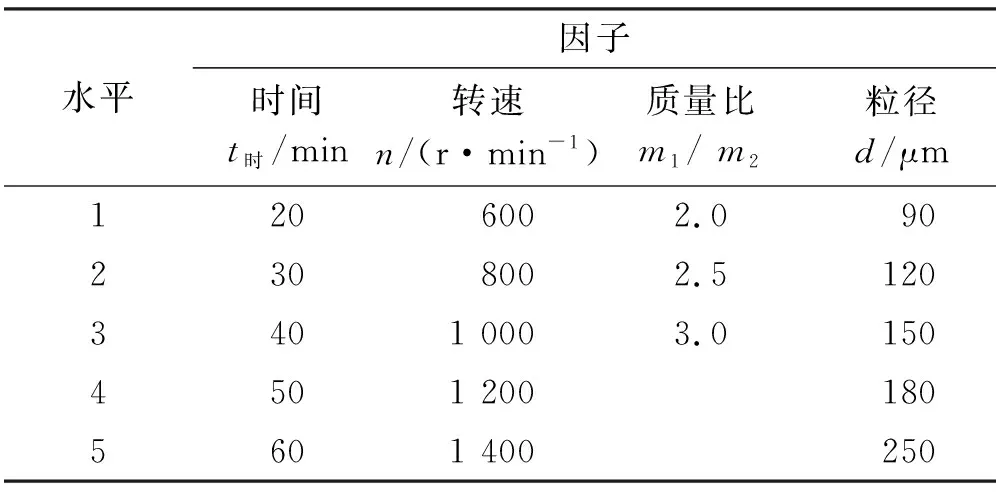
表1 试验因子水平

2 试验结果与分析

2.1 逐步回归分析

逐步回归的基本思想在于逐个引入变量。每次引入对Y影响最显著的自变量，并对方程中的原有变量进行检验，当原引入的变量由于后面变量的引入而不再显著时，要将其剔除。变量的引入和剔除都要进行显著性检验，以确保回归方程中只包含显著的变量。最终得到的方程中，既不漏掉对Y影响显著的变量，又不包含对Y影响不显著的变量[7-8]，基本步骤如图4所示。

图4 逐步回归步骤

自变量X1，X2，X3，…，Xn-1，Xn与因变量Y具体的逐步回归步骤为：

(1)对变量进行回归分析，计算出Y与X1，X2，X3，…，Xn-1，Xn之间的样本拟合度R2。

(2)按照R2的大小，对每一个X1，X2，X3，…，Xn-1，Xn进行排列。

(3)选取最大的R2变量Xj建立回归分析模型：

(1)

引入第2大的R2变量Xi进行回归分析，建立模型：

(2)

式中：a1、b1是常数,a2、b2是Xj的系数，b3是Xi的系数，F1、F2、R1、R2是检验值，tj、ti指的是当前已有的变量。

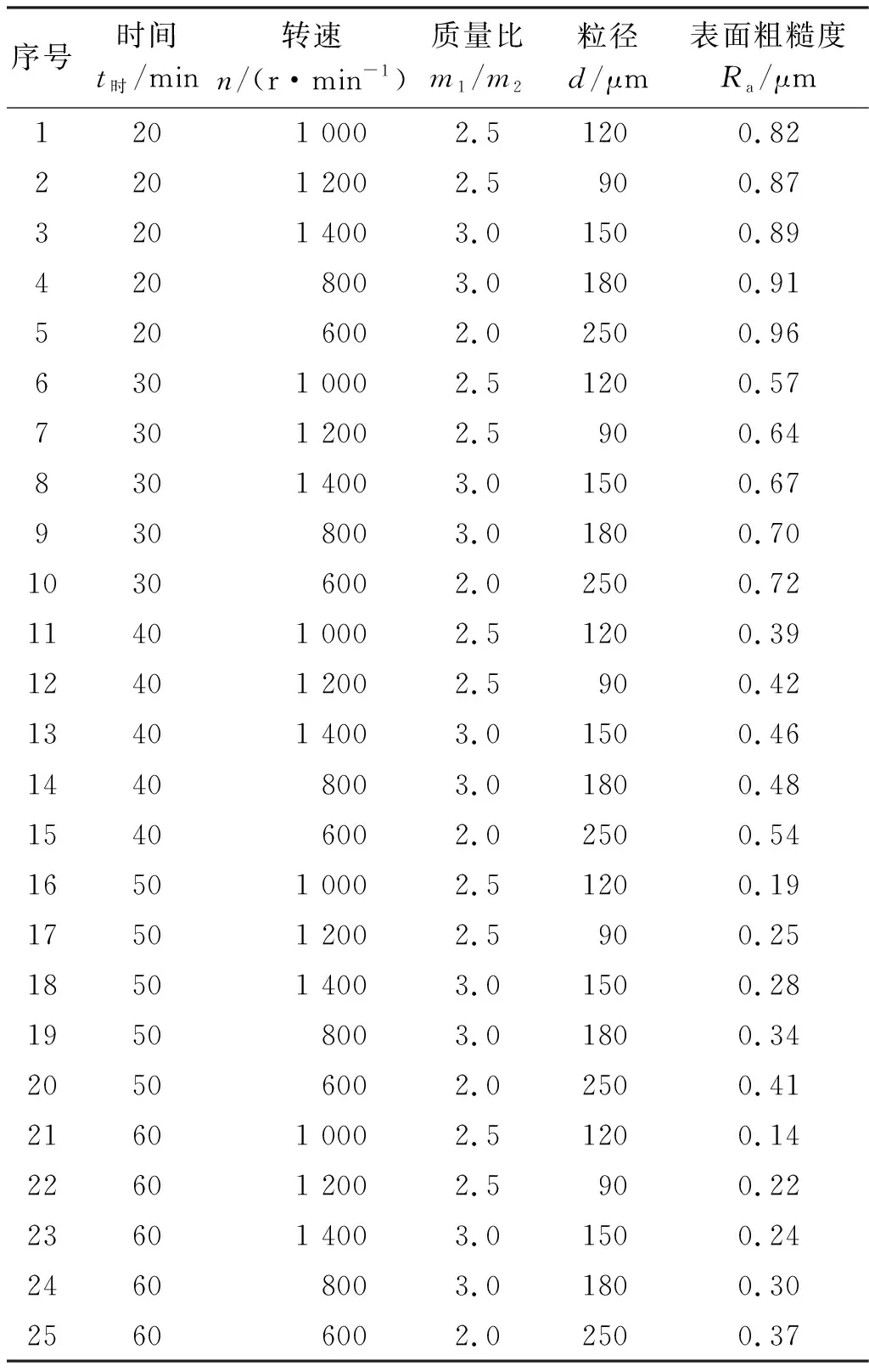
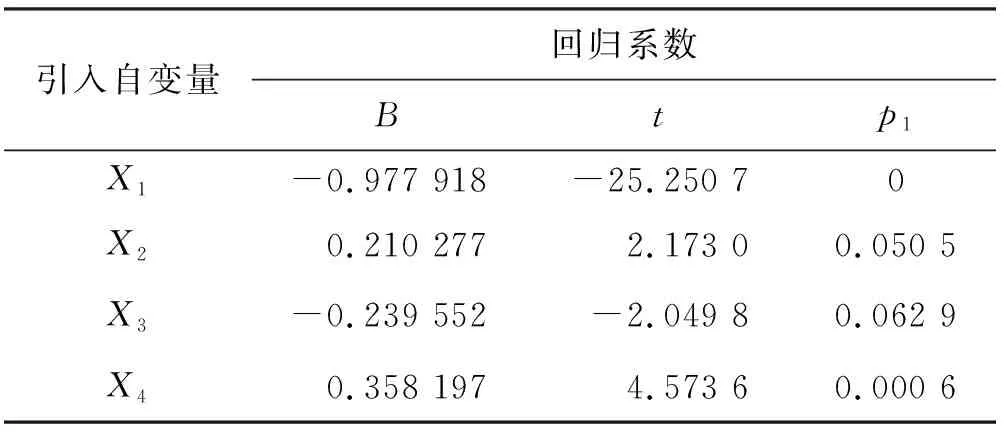
若R1

(4)重复上一个步骤，直到所有的自变量X1，X2，X3，…，Xn-1，Xn全部被筛选，则计算结束。

2.2 建立数学模型

按照表1中分配的试验因子水平进行25组试验，试验结果如表2所示。

表2 试验结果

因变量和自变量之间存在非线性关系[9-11]。因此，对试验结果取对数，使其线性化，令X1=lgt，X2=lgn，X3=lg(m1/m2)，X4=lgd，Y=lgRa。

对经过对数化处理的数据进行残差分析，剔除异常值，重复这个步骤，直到不再出现异常值。残差分析剔除表2中的7、8、16、17、18、21、22、23号试验数据，最后得到的残差分布图如图5所示。

图5 残差分布图

对剔除掉异常值的数据进行逐步回归分析。引入自变量X1、X2、X3、X4，其逐步回归分析结果如表3所示，模型检验参数如表4所示。

表3 逐步回归分析结果

表4 模型检验参数

表3中的B值为自变量X1、X2、X3、X4的系数，t值和p1值用于自变量的显著性检验，p1值越接近于0，说明影响越显著。表4中的R2和Adj-R2用于模型拟合程度检验，F值和p2值用于模型的显著性检验，常数作为模型中常数项的系数。

2.3 数学模型的检验与验证

对逐步回归方程进行检验：

(1)R检验：回归方程的R2=0.983 358，R2越接近于1，说明模型的拟合程度越好。因此，本模型的拟合程度较好。

(2)F检验：模型的F值为177.27，经查表得F0.01(4，12)= 5.41，177.27 >> 5.41。所以，经过F检验，说明回归方程在α=0.01程度上是显著的。

(3)t检验：对各个变量进行t检验，经查表得t0.05(12)= 1.782，而在α=0.05显著水平上，显著的有t1=-25.250 7，t2=2.173 0，t3=-2.049 8，t4=4.573 6。

表3回归系数中的B值作为各自变量的系数，表4回归系数中的常数作为常数项的系数，Y作为因变量，于是可以得到回归方程：

Y= -0.977 918X1+0.210 277X2-

0.239 552X3+0.358 197X4-0.084 490

(3)

即可得到最终表面粗糙度预测模型：

(4)

采用式(4)的回归预测方程，进行6组试验，以验证模型的准确性，试验参数如表5，对比结果如表6所示。

表5 6组验证试验参数

表6 预测模型的试验验证

由表6可知：运用逐步回归建立的预测模型的相对误差绝对值能够控制在7%以内，能够较好地预测磁粒研磨加工后的轴类零件表面粗糙度。图6为6组验证试验的表面粗糙度及工件表面的微观形貌图。

(a)Ra=0.850 μm(b)Ra=0.580 μm(c)Ra=0.410 μm(d)Ra=0.300 μm(e)Ra=0.270 μm(f)Ra=0.340 μm图6 表面粗糙度及微观形貌Fig. 6 Roughness and micromorphology

3 结论

通过增加外部磁极数量的方法，防止加工时磁性磨料的流失，在此磁粒研磨工艺下，对20CrMnTi材质的轴类零件进行加工，对其表面粗糙度和加工参数进行逐步回归分析得到表面粗糙度的预测模型，相对误差绝对值能够控制在7%以内，具有较好的预测能力。