基于spike-angle 图和Fourier 变换的磨粒图像形状特征提取*

鲁华杰 郭恒光 刘文彪

（海军航空大学岸防兵学院 烟台 264001）

1 引言

磨粒分析技术是一种有效的机械设备状态监测方法，通过采集机械设备油液中的磨粒，分析磨粒所属的类型，判断设备的主要摩擦方式，为机械设备的维护和保养提供决策依据。磨粒的形状特征是判断磨粒所属类型的重要依据，不同类型的磨粒，由于磨损类型和形成机理不同，会表现出不同的形状特征，目前应用较多的磨粒形状特征包括磨粒的基本几何参数［1~2］、傅里叶描绘子［3~6］、分形维数［7~11］和Spike［12~14］参数等。

M.G.Hamblin 和G.W.Stachowiak 在1995 年 提出spike参数，它是在分形维数的基础上，对磨粒轮廓进行更细致的描述，在每一步的起点与终点之间，引入两点之间磨粒轮廓上的某一点，这3 个点构成一个“Spike”，然后对Spike 值进行计算，最后将考虑步长大小和数量情况下的Spike平均值作为Spike参数。

Spike 参数反映了该磨粒轮廓的角度变化状况，该参数越大，磨粒轮廓越尖锐、磨损作用越大。基于Spike 参数的思想，本文提出了spike-angle 参数和spike-angle 图的概念。首先计算磨粒的轮廓点在不同步长下的spike-angle参数，遍历磨粒的所有轮廓点，得到磨粒的spike-angle 图，spike-angle图的行表示在单一步长下，磨粒所有轮廓点的spike-angle 参数，反映了磨粒轮廓的整体特征，spike-angle 图的列表示磨粒的单个轮廓点在不同步长时的spike-angle参数，反映了磨粒轮廓的局部特征。然后对spike-angle 图的行和列分别进行傅里叶变换，并对傅里叶变换系数的幅值进行归一化。最后对每一阶归一化后的傅里叶变换系数幅值进行直方图统计，得到反映磨粒轮廓整体特征和局部特征的直方图，以这两个直方图作为磨粒的形状特征。

2 Spike参数

Spike 参数的计算类似于分形维数的计算，如图1所示，以轮廓点A为起点，按一定的步长找到轮廓点B 作为终点，其中步长是指起点和终点之间磨粒轮廓像素点的数量。在A 和B 之间的轮廓上寻找一点P，三个点构成一个三角形区域ΔAPB，称之为“Spike”，用来描述磨粒位于起点和终点之间的轮廓。为了描述ΔAPB 的大小和尖锐程度，定义了Spike值Sv，如下式所示：

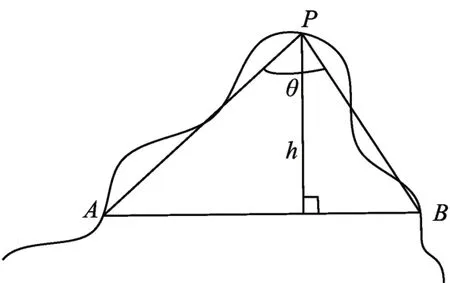
图1 Spike参数计算原理图

式中：θ为ΔAPB 中PA和PB之间的夹角，h为ΔAPB顶点P到边AB的垂直距离。

Spike参数SP按下式计算：

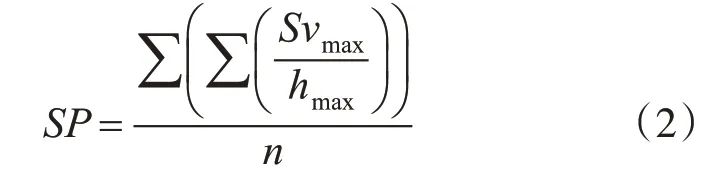
式中：Svmax=max(cos(θ2)h)；m为在给定步长时，有效的Sv的数量；n为所使用的不同步长的数量。

3 spike-angle参数和spike-angle图

由spike 参数的定义可以看出，Spike 参数的实质为通过起点和终点间三角形区域ΔAPB顶点P的角度平均值来描述磨粒轮廓的特征。但是在磨粒类型识别时，若仅使用Spike 参数作为磨粒形状特征时，识别效果不佳。基于Spike参数的思想，本文提出了基于改进的Spike 参数，称之为spike-angle参数（spike-angle parameter）。

为了使最后获得的形状特征具有尺度不变性，首先对磨粒二值图像中磨粒大小进行归一化，磨粒大小归一化到Q，也就是说磨粒二值图像强度的和为Q。然后提取磨粒的轮廓，并对磨粒轮廓点进行均匀采样，得到N个轮廓点，最终的磨粒轮廓为

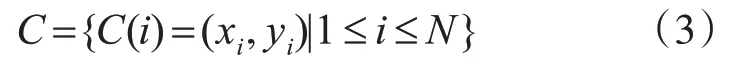
以第i个轮廓点为起点A，步长为s（最大步长为M），得到终点B，则A和B之间的轮廓点序列为

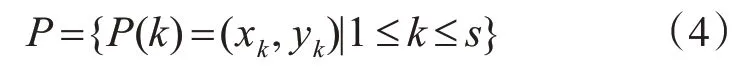
A点、B点和P点序列构成s个三角形，根据式（1）计算每一个三角形的Spike值。

则第i个轮廓点，在步长为s时的spike-angle 参数的定义为

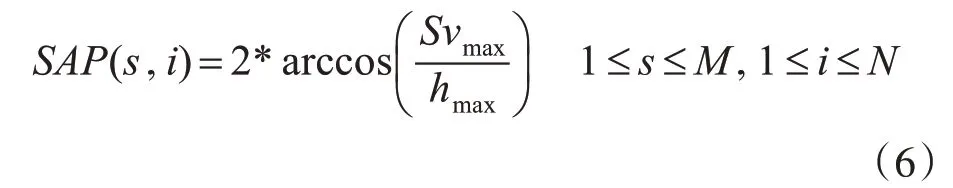
式中：Svmax=max(cos(θk2)hk)；hmax为Sv最大时，对应的三角形区域的顶点P到边AB的垂直距离。

依次取磨粒的每一轮廓点为起点，计算其在不同步长下的spike-angle，得到所有轮廓点在不同步长下的spike-angle，所有spike-angle 参数构成一个矩阵，将其定义为spike-angle图。

spike-angle图的行表示在单一步长下，磨粒所有轮廓点的spike-angle参数，反映了磨粒轮廓的整体特征，spike-angle图的列表示磨粒的单个轮廓点在不同步长时的spike-angle参数，反映了磨粒轮廓的局部特征，同时由于计算spike-angle时采用了不同的步长，spike-angle图又反映了磨粒轮廓的多尺度信息。因此，spike-angle图包含了磨粒的整体形状特征、局部形状特征以及多尺度形状特征。Spike-angle参数不受磨粒图像旋转和平移的影响，而且由于对磨粒图像强度进行了归一化处理，所以spike-angle图具有平移、尺度和旋转不变性。

图2（a）、图3（a）和图4（a）分别为三种典型的磨粒：切削磨粒、严重滑动磨损磨粒和疲劳磨损磨粒，图2（b）、图3（b）和图4（b）所示分别为三种典型的磨粒对应的spike-angle 图。由图2（b）、图3（b）和图4（b）可以看出，不同类型的磨粒，对应的spike-angle图区别很显著，而且spike-angle图包含了磨粒的整体形状特征、局部形状特征、以及多尺度形状特征，因此根据磨粒的spike-angle图对磨粒形状进行识别是可行的。spike-angle 图的数据量大，直接用于磨粒形状识别，效率低，需要耗费大量时间，这就需要研究从spike-angle 图中提取信息，作为磨粒的形状特征。

图2 切削磨粒及其spike-angle图

图3 严重滑动磨损磨粒及其spike-angle图

图4 疲劳磨损磨粒及其spike-angle图

4 磨粒图像形状特征提取

在形状的轮廓描述和形状识别中，广泛使用傅里叶描述子，实现使用少数低价系数得到高质量的形状描述的效果。本文对spike-angle 图的行和列分别进行傅里叶变换，提取spike-angle图中提取信息，进而得到磨粒的形状特征。

对spike-angle 图的第s行做傅里叶变换，相当于对磨粒的整体轮廓在步长为s时的spike-angle值序列做傅里叶变换，得到的傅里叶变换系数Global_as，n为

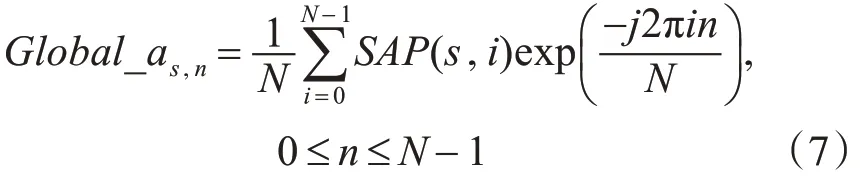
对spike-angle 图的第i列做傅里叶变换，相当于对磨粒的第i个轮廓点在所有步长下的spike-angle值序列做傅里叶变换，得到的傅里叶变换系数Local_ai，n为

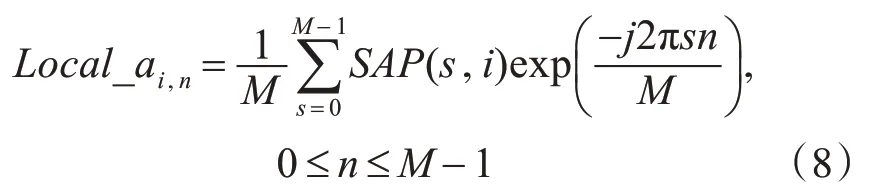
为了使得最后的形状特征具有平移、尺度和旋转不变性，取傅里叶变换系数的幅值并除以第一个系数的幅值，得到归一化的系数幅值。因为少数低阶系数可对形状进行高质量的表示，因此可采用前m个归一化后的系数幅值，作为磨粒形状的特征，即：

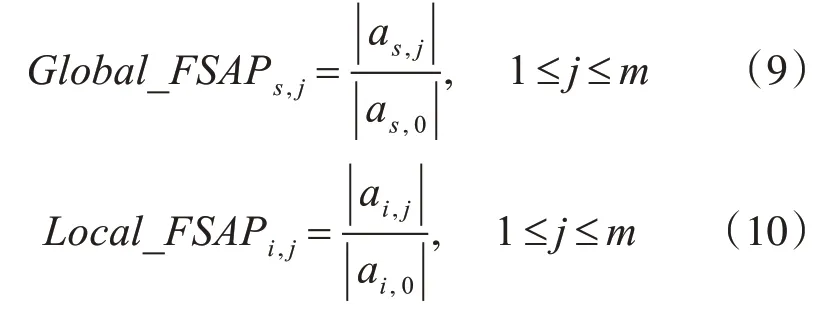
由于傅里叶变换的第一个系数的幅值远大于其他系数的幅值，因此归一化后的傅里叶系数Global_FSAPs，j和Local_FSAPi，j的 取 值 区 间 为(0，1)。

图5 为归一化的傅里叶变换系数幅值曲线，其中实线、点线和虚线对应的分别为切削磨粒、严重滑动磨损磨粒和疲劳磨损磨粒。图5（a）~（d）分别为对spike-angle图的行做傅里叶变换之后，得到的前4 阶归一化系数幅值，图5（e）~（h）分别为对spike-angle 图的列做傅里叶变换之后，得到的前4阶归一化系数幅值。由图5 中的每个图中的曲线对比都可以看出，不同磨粒的归一化系数幅值差别是比较明显的，这也从一个角度证明了本文提出的spike-angle参数和spike-angle图是可行的，并且包含了磨粒形状的信息，可以从中提取磨粒的形状特征，用于磨粒类型识别。

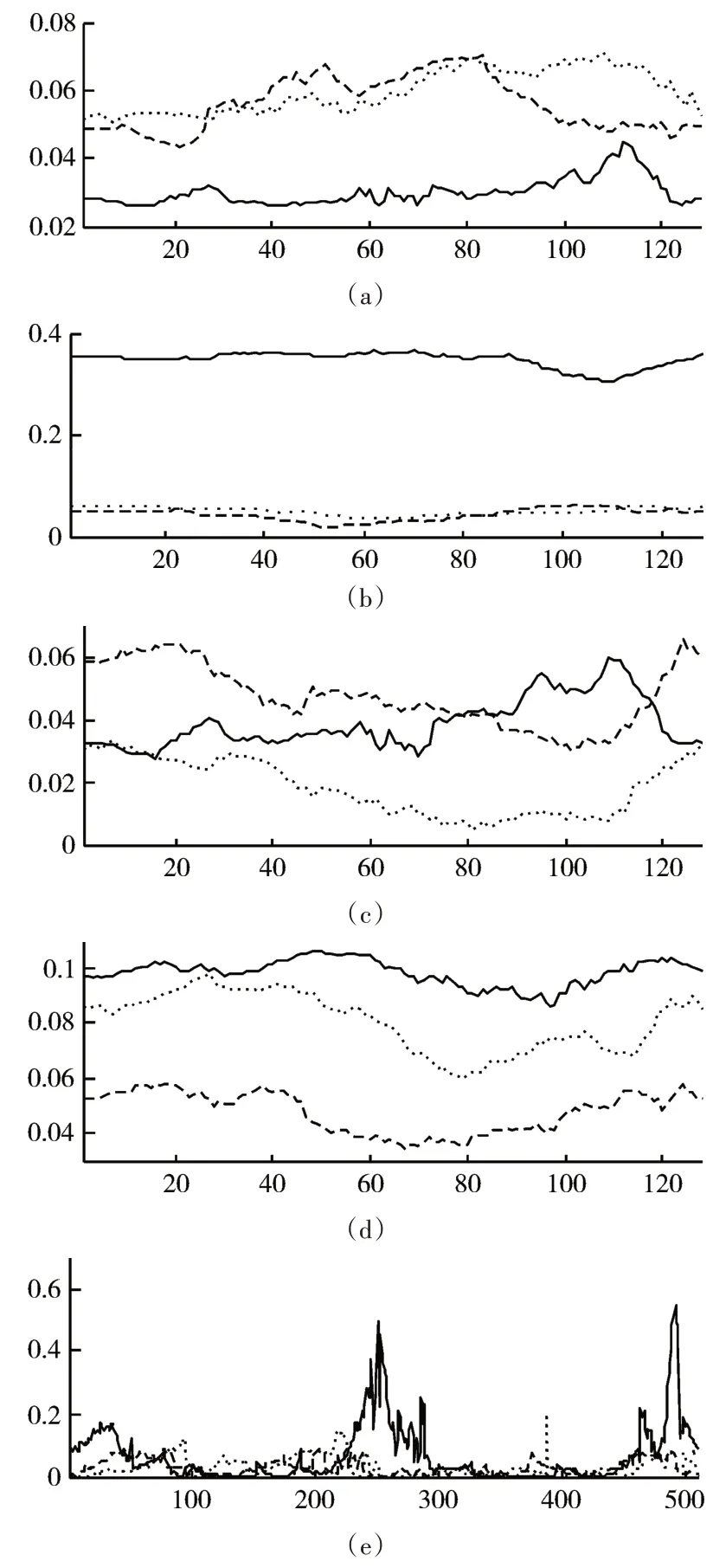
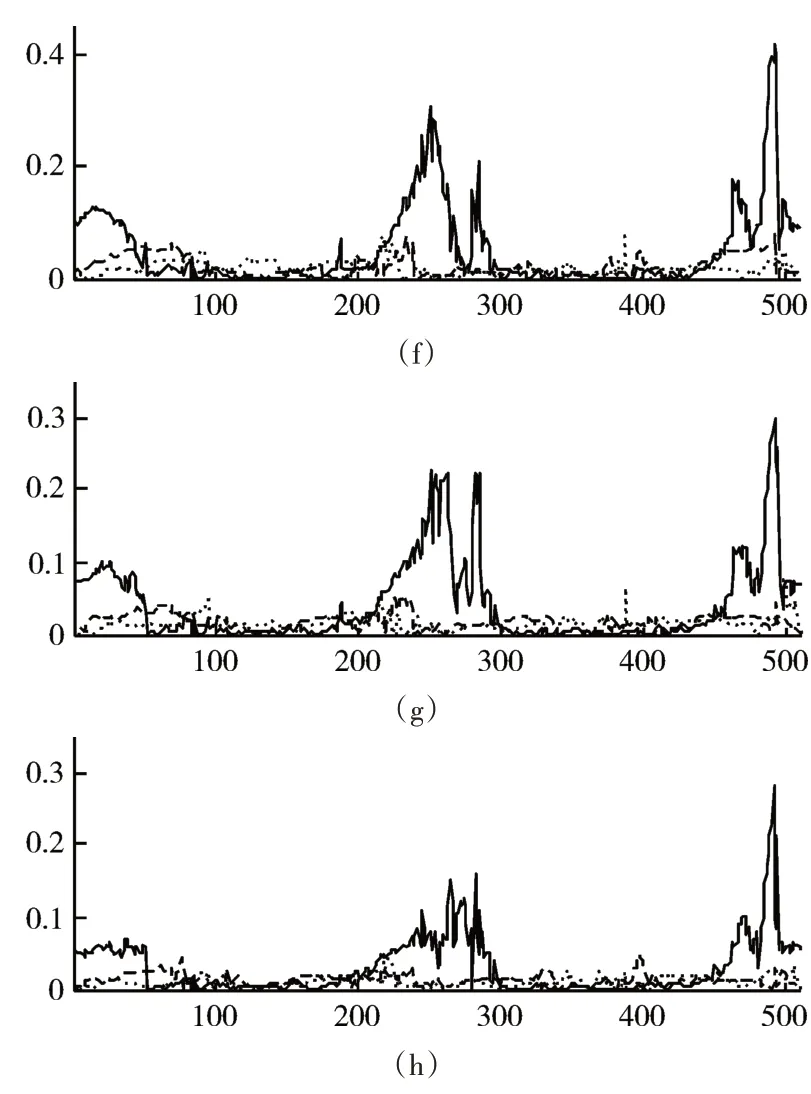
图5 归一化的傅里叶变换系数幅值

虽然只采用前m个归一化后的傅里叶系数幅值，但是得到的系数矩阵仍然较大，也不能直接用作磨粒的形状特征，下面就对每一阶归一化后的傅里叶变换系数幅度进行直方图统计，以得到的直方图作为磨粒的形状特征。

由于每一阶归一化后的傅里叶系数幅值取值区间差别比较大，因此无法采用统一的区间划分对所有的系数幅值进行直方图统计。本文采用了以下的方法：采集大量的不同类型的磨粒，并用本文的方法得到所有磨粒的归一化的系数矩阵Global_FSAP和Local_FSAP，确定Global_FSAP矩阵和Local_FSAP矩阵的每一个列的最大值，即每一阶归一化系数幅值的最大值。然后将每一阶系数幅值的取值区间划分为8 个小区间，即将0 到每一阶系数幅值的最大值之间的区间划分为8 个小区间，根据相应的划分区间，分别对每一阶归一化后的傅里叶系数幅值进行直方图统计，并对直方图作归一化处理，则得到的直方图为

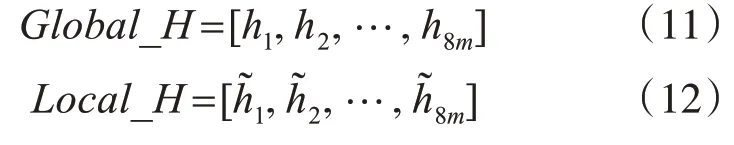
其中，直方图的前8 个分量对应的是系数矩阵的第1 列系数的归一化直方图，直方图的第9 个分量到第16 分量对应的是系数矩阵的第2 列系数的归一化直方图，直方图的第8m-1 个分量到第m分量对应的是系数矩阵的第m列系数的归一化直方图。最后以所得到的两个直方图Global_H和Local_H作为磨粒的形状特征，分别称之为整体直方图特征和局部直方图特征。

图6（a）、7（a）和8（a）分别为三种典型磨粒的整体直方图特征，图6（b）、7（b）和8（b）分别为三种典型磨粒的局部直方图特征，提取直方图特征时，对归一化傅里叶系数幅值矩阵的前4 阶系数进行直方图统计。由各种典型磨粒的整体直方图特征和局部直方图特征的对比可以看出，不同类型磨粒的直方图特征区别是很明显的，各阶归一化傅里叶系数幅值出现的区间以及频率相差也比较大，因此采用整体直方图特征和局部直方图特征作为磨粒的形状特征是可行的。

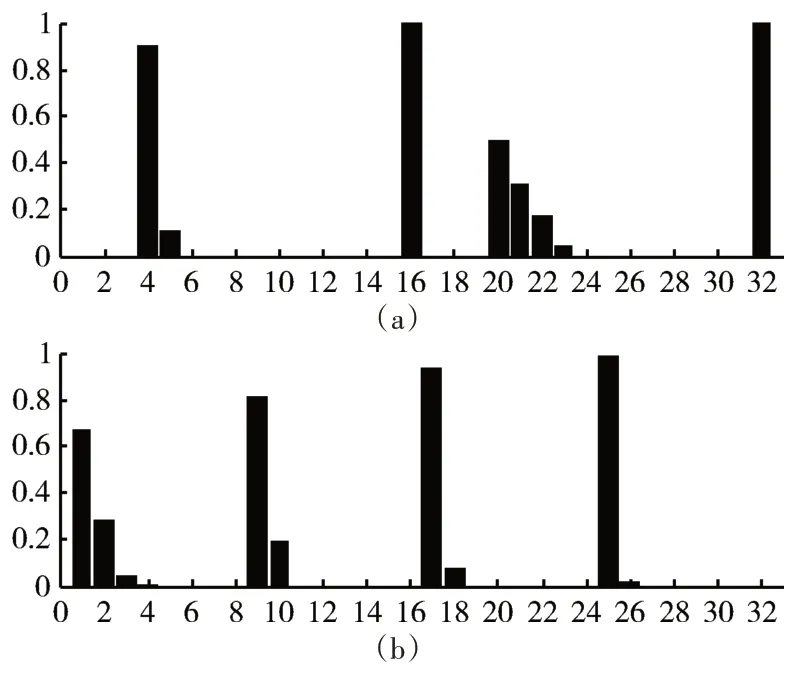
图6 切削磨损磨粒直方图特征

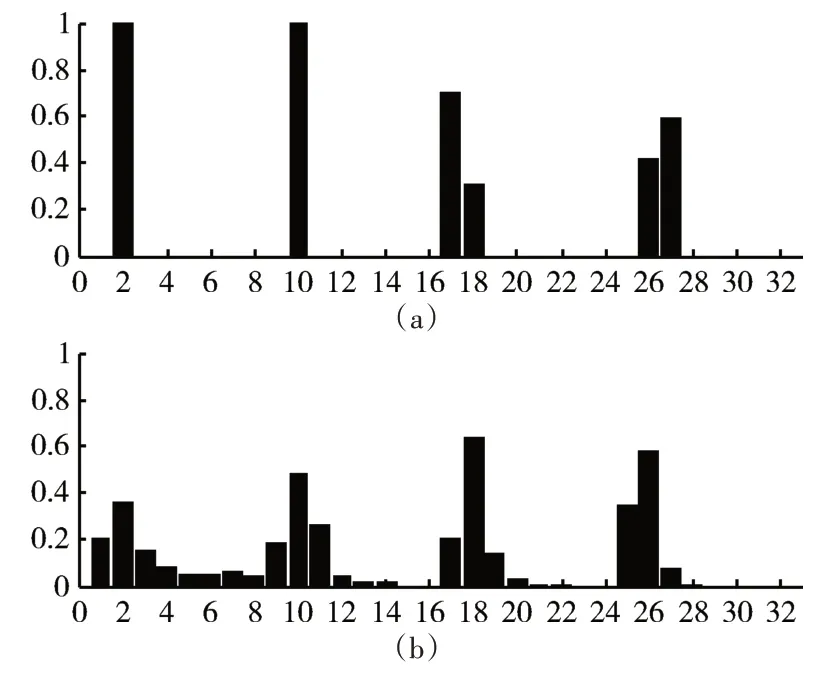
图7 严重滑动磨粒直方图特征

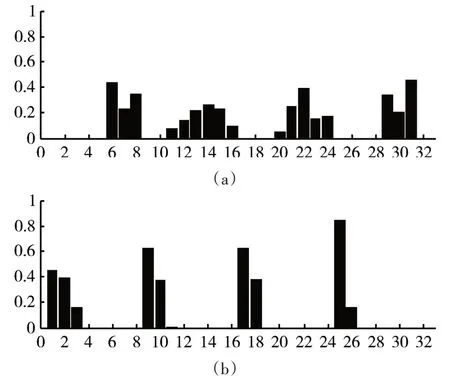
图8 疲劳磨损磨粒直方图特征

5 磨粒图像类型识别

以某型导弹发射车发动机为监测对象，定期采集其发动机润滑油，并分离出其中的磨粒，然后使用光学显微镜拍照获取磨粒图像。根据研究需要，本文对其中的正常磨粒、切削磨粒、严重滑动磨损磨粒和疲劳磨损磨粒进行类型识别研究。

每种类型的磨粒分别获得30个样本，将120个样本随机分为两组，其中1组70个样本用于训练算法，50 个样本用于算法测试。第一步根据本文提出spike-angle参数计算方法，得到每个磨粒图像的spike-angle图；然后对spike-angle图的行和列分别进行傅里叶变换，并对傅里叶变换系数幅值进行归一化；最后对得到归一化傅里叶系数幅值矩阵按列进行直方图统计，获得磨粒图像的形状特征。根据磨粒图像的形状特征，采用支持向量机的方法［15］，对磨粒类型进行识别，并与其它形状特征提取方法做比较。

由于SVM 是一种二元分类器，只能对两种类型进行识别，当对多种磨粒类型进行识别时，必须构造一种多元分类器才能进行多种磨粒类型的识别。本文采用1 对1 的方法构造多元分类器，对任意两个类型磨粒，训练一个SVM 将二者分开。因此，对于N元分类问题，需要构造N(N-1) 2 个SVM。本文对4 种磨粒类型进行识别时，需要建立和训练的SVM为6个。

使用磨粒样本对多元分类器训练后，在不改变模型参数的情况下，采用另一组的50 个样本对分类器进行测试。测试结果如表1 和表2 所示，其中表1 为训练实验结果，表2 为测试结果。由表1 和表2 可以看出，本文提出的基于spike-angle 图的磨粒形状特征提取方法，优于其他几种常用的形状特征。其中，Spike 参数和简单的几何参数对应的识别率较低，这两个形状特征不具有平移、尺度和旋转不变性，而且只利用简单的数值来表征磨粒形状，不能充分反映磨粒的形状特征。Zernike 矩和傅里叶描绘子对应的识别率要高于Spike参数和简单的几何参数，这两个形状特征都具有平移、尺度和旋转不变性，反映了磨粒形状的整体特征，也是应用较多的形状特征。本文提出的磨粒形状特征，包含了磨粒的整体形状特征、局部形状特征和多尺度形状特征，能够充分利用磨粒的形状信息，因此在磨粒类型识别中能够取得好的效果。

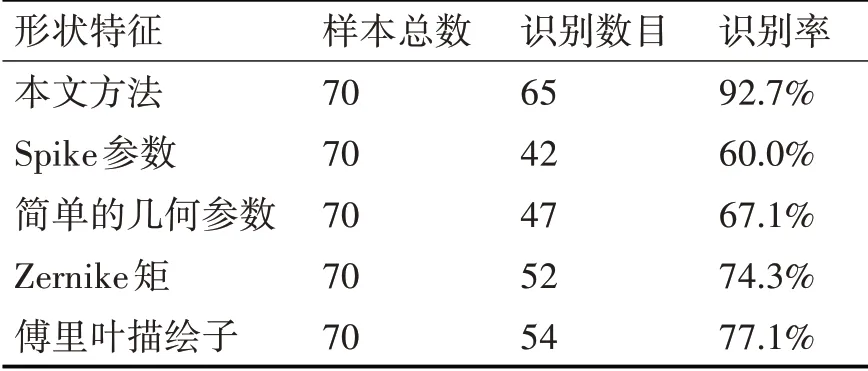
表1 磨粒类型识别训练实验结果

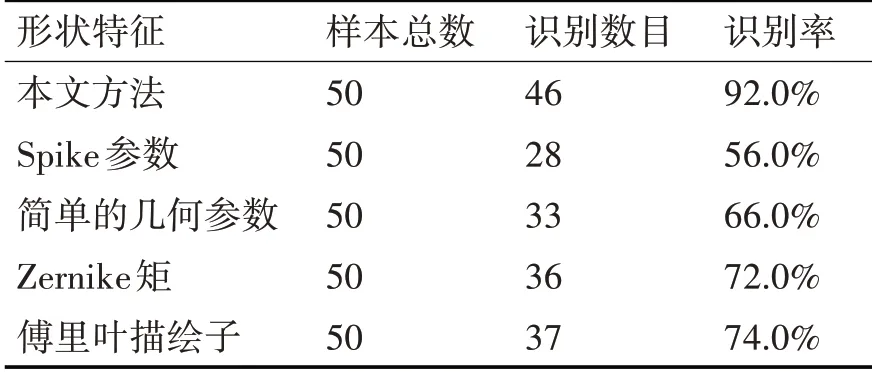
表2 磨粒类型识别测试实验结果

6 结语

本文根据磨粒spike 参数的计算思想，提出了spike-angle值和spike-angle图的概念，并且研究了基于spike-angle 图的磨粒形状特征提取方法。该方法首先计算磨粒的所有轮廓点在不同步长时的spike-angle 值，得到磨粒的spike-angle 图；然后对spike-angle图的行和列分别进行傅里叶变换，并对得到的傅里叶变换系数幅值进行归一化处理；最后对每一阶归一化的傅里叶变换系数幅值进行直方图统计，以获得的整体直方图特征和局部直方图特征作为磨粒的形状特征。本文所提的磨粒形状特征提取方法，包含了磨粒形状的整体信息、局部信息和多尺度信息，磨粒类型识别训练实验结果和磨粒类型识别测试实验结果也表明了本文所提的方法的有效性。