管道对称性对后混合磨料水射流喷嘴流场的影响

吴 伟，唐 勇，袁 硕，李明杰

（1.长沙矿山研究院 高压水射流研究所，长沙 410012；2.湖南大学 机械与运载工程学院，长沙 410082）

0 引言

磨料水射流是利用高速高压状态的水在喷嘴混合腔内部与低速状态的磨料颗粒混合，从而带动磨料粒子高速运动，利用混合形成的高速固液二相流对靶体进行冲击碰撞，通过调节喷嘴出口的固液二相流速度及流量等，实现对靶体的切割、抛光、清洗等功能［1］。与传统加工方式相比，磨料水射流最主要的优势在于冷态作业、节能环保。磨料水射流加工作业时，对周边环境不产生任何污染，产生的水和磨料颗粒经简单处理可再循环利用。在对某些特殊材料加工作业时，磨料水射流有着不可替代的作用，如玻璃、橡胶和塑料等。传统的加工方式是利用刀具的刀刃与材料垂直接触，通过施加垂直于刀刃的力与沿切割面平行的往复运动，实现材料的切割，但这种加工方式会在刀刃附近因摩擦产生大量热量，或导致刀具与材料黏合，或在材料内部生产较大内应力，影响工件性能。

喷嘴是磨料水射流技术系统中最关键的一个部件，此部件由于长期受高压水流及高速磨料的冲击碰撞，易在其内部发生磨损、沉积、堵塞等情况，严重影响磨料水射流的工作效率［2］。提高喷嘴混合腔内部的高速水流与磨料浆体的混合均匀性，是减少喷嘴内部磨损，同时提高磨料水射流工作效率的一种主要方法。目前对磨料水射流喷嘴研究成果有：田家林等［3］通过对喷嘴的不同类型、长度以及锥角角度进行数值仿真和试验验证，得出了锥直形喷嘴为较好结构。刘国勇等［4］利用数值模拟得到了喷嘴内部有无圆锥挡板及圆锥挡板的不同物理模型参数对喷嘴出口磨料均匀性的影响。黄飞等［5］设计了5种不同形状的喷嘴进行高压水射流冲击力试验，试验结果表明圆形喷嘴的射流集束性最好，三角形、十字形及椭圆形喷嘴集束性最差。NARESH等［6］建立了磨料射流去冲击不锈钢靶材的有限元模型，研究了磨料颗粒碰撞角度和速度对撞击靶体形成的深度和冲蚀速率等影响。AHMED等［7］通过数值研究，探究磨料水射流的切割性能主要取决于磨粒的速度、冲击角和磨粒与被切割工件的物理特性，以及数值结果表明对于大曲率半径的颗粒有滑动或靠近切割表面的趋势。

为了改善喷嘴内部的磨料与高速水流的混合情况及射流速度，本文设计了4组除磨料管道对称性不同、其余参数均相同的后混合喷嘴，通过在相同工况条件下进行数值模拟，探究了磨料管道的对称性对后混合磨料水射流喷嘴内外流场的具体影响。

1 流体基本方程和喷嘴物理模型

1.1 流体基本方程

喷嘴内部是高压水与磨料颗料的高速紊流，由于磨料颗粒粒径细小，可忽略磨料颗料对水流的影响作用，将磨料入口处的磨料与水混合后的浆体看作连续相，且最初时喷嘴内外均充满空气，所以流体在喷嘴内外的流动是水-磨料-空气的三相流动。该三相流动的连续性方程为［8］：

式中 ρ——流体密度；

t——时间；

u，v，w——速度矢量在坐标轴x，y和z方向的分量。

三相流动中流体的动量对时间变化率的大小等于外界作用在该流体上各种力之和，可导出流体沿各坐标轴X，Y，Z的运动方程如下［8］：

式中 div——散度；

p——流体微元体上的压力；

τ——流体微原体表面的黏性切应力τ的分量；

F——流体微元体上的体积力。

计算机直接求解三维瞬态的运动方程对计算机内存及运算速度都有很高的要求，目前常用的方法为湍流k-ε方程对瞬态运动方程做时间平均处理［9］。

湍动能k方程为：

式中xi，xj——流体微元体在坐标轴x，y方向上的坐标；

μ——黏度系数；

μt——涡黏性系数；

Cμ——经验常数；

ε——单位质量的湍流脉动动能的耗散率。

湍流耗散率ε方程为：

式中V——速度矢量；

C1ε，C2ε——系数。

1.2 喷嘴模型

图1 磨料管非对称型喷嘴物理模型Fig.1 Physical model of asymmetric nozzle of abrasive pipe

表1 喷嘴几何参数Tab.1 Geometric parameters of the nozzle mm

保证磨料管道沿磨料浆体流动方向的总横截面积不变，通过改变磨料管道的数量，将磨料管非对称型喷嘴改变为1组磨料管对称型喷嘴，两组磨料管对称型喷嘴及环形磨料管对称型喷嘴。抽取各组喷嘴的流道域及添加直径为90 mm，高为90 mm的外流场计算域，得到各喷嘴的总计算域模型如图2所示。

图2 喷嘴计算域模型Fig.2 Diagram of nozzle computational domain model

2 数值计算

2.1 网格无关性证明

为了求解计算域内所建立的连续方程、运动方程及湍流k-ε方程等复杂偏微分方程，计算域网格离散后可以使计算得到的数值解接近于原方程的解析解，但网格的种类、数目及质量影响着数值计算的运算速度、精确度及稳定性。

将图1所示的非对称型喷嘴进行网无关性试验，高压水入口速度为100 m/s，磨料浆体入口速度为10 m/s，通过入口及出口的面积求出理论出口流速，然后设置不同的网格数量级进行数值计算，得出的数值解与理论解偏差见表2。随着网格数量级的增加，计算准确度有了明显提高，但网格数量级增至60万以后，数值计算的准确度提升不明显，只在小范围波动；网格数量级在20万～40万时，数值计算准确度不理想，综合考虑数值计算准确度、计算速度及计算机等硬件设备，网格数量级确定在60万。

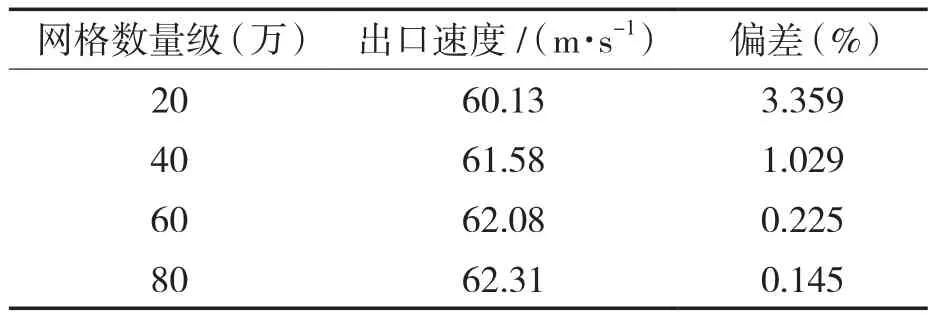
表2 网格无关性证明Tab.2 Grid independence verification

2.2 计算设置

后混合磨料水射流是复杂的三相紊流流动，其中高压水相和空气相是流体相，磨料颗粒是固态颗粒相，但在工程实践中磨料颗粒常采用与水混合后形成的浆体作为通入磨料管道的原料见参考文献［4，10-14］，在数值计算中，模型基于下列假设：（1）磨料入口处进入的是水和磨料均匀混合后的连续相。（2）忽略磨料颗粒间的相互作用，以及磨料颗粒对水相的影响。（3）水为理想不可压缩流体，磨料颗粒视做理想小球。

该喷嘴的工况为：高压水泵的额定压力为35 MPa，磨料浓度50%，磨料粒径80目，砂浆泵的额定压力为0.1 MPa。边界条件设置如下。（1）高压水入口：设置为速度入口，速度大小为260 m/s，压强为标准大气压。（2）磨料入口：设置为速度入口，高压水和磨料的速度均为10 m/s，磨料的体积分数为0.5，压强为标准大气压。（3）喷嘴出口：设置为压力出口，出口压力为标准大气压。（4）喷嘴壁面：设置为无滑移边界条件，近壁面区域采用标准壁面函数法计算。

根据泰勒级数理论，一阶迎风格式和混合格式在对控制方程进行离散时，易引起假扩散发生，且计算精度只有一阶截差，为了提高计算精度，采用具有二阶截差的二阶迎风离散格式，同时采用了基于压力场-速度场关联算法的Phase coupled simple算法和Realizablek-ε方程，其他参数默认。设置初始化的空气占流体域的体积分数为100%，流体材料物理属性参数设置见表3。

表3 流体材料物理属性参数Tab.3 Physical parameters of the fluid material

3 仿真结果及分析

3.1 磨料管非对称型喷嘴

磨料管非对称型喷嘴的磨料浆体是通过单根管道流入混合腔与高速流动的水进行混合，由于磨料管道的管径是远大于红宝石水喷嘴的管径，这使得具有一定流量、动量的磨料浆体从单一方向流入后，直接在喷嘴混合腔内与高速水流发生碰撞混合，高速水流会发生一定弯曲，向着磨料浆体来流方向偏移，图3所示为非对称型喷嘴内外流场的水速云图。

图3 非对称型喷嘴的水速云图Fig.3 Water speed nephogram of asymmetrical nozzle

从图3可得，水速最高的部分是集中在喷嘴中轴线附近，但因高速水流的偏移，导致与喷嘴混合腔内壁发生碰撞，高速水流的能量有一定损失。

在喷嘴混合腔内，来自高压水入口的水流速度远大于进入混合腔内的磨料浆体的速度，高压水流会对磨料浆体产生卷吸作用，非对称型喷嘴的混合腔内磨料速度矢量如图4所示。从图4可见，由于磨料浆体是从单一的磨料管进入，在高速水流靠近磨料管侧会因卷吸作用形成一个大的涡旋区，而高压水流附近的其余位置则因磨料浆体的数量较少，形成的漩涡区小，甚至不生成漩涡区。

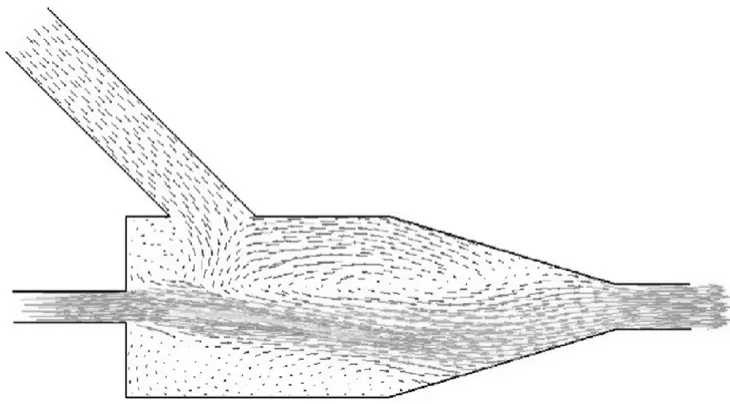
图4 非对称型喷嘴的磨料速度矢量Fig.4 Abrasive speed vector of asymmetrical nozzle

图5，6分别示出非对称型喷嘴在纵截面的磨料体积分数云图和距离喷嘴出口40 mm处、直径为12 mm的射流核心段横截面磨料体积分数云图。

图5 非对称喷嘴的磨料体积分数云图（纵截面）Fig.5 Abrasive volume fraction nephogram of asymmetrical nozzle（longitudinal section）

图6 非对称喷嘴的磨料体积分数云图（横截面）Fig.6 Abrasive volume fraction nephogram of asymmetrical nozzle（cross section）Abrasive volume fraction contour of asymmetrical nozzle（cross section）

从图5，6中可见，由于磨料管道的非对称性，导致喷嘴混合腔内的磨料浆体与高速水流混合效果并不理想，磨料浆体向一侧聚集，外流场的射流核心段内的磨料浆体分布不均。

3.2 1组磨料管对称型喷嘴

1组磨料管对称型喷嘴是在非对称型喷嘴的结构上，保证磨料管道总横截面积不变的情况，用2个对称的磨料管道去代替1个磨料管道形成的。

由于布置为对称型磨料管道，单根磨料管道内的磨料浆体流量和动量较非对称型磨料管道内的磨料浆体有了一半的减少，对混合腔内的高速水流的冲击影响有了明显减弱，且磨料浆体对高速水流的冲击碰撞也因为对称性的原因可相互部分抵消。图7示出1组磨料管对称型喷嘴的水速云图，与图3相比，高速水流没有发生明显的偏移和弯曲，避免了高速水流直接冲击混合腔，减少了能量损失，提高了射流利用率。

图7 1组磨料管对称型喷嘴的水速云图Fig.7 Water speed nephogram of a set of symmetrical nozzles of abrasive pipes

图8示出1组磨料管对称型喷嘴混合腔的磨料速度矢量，从图中可知高速水流对磨料浆体的卷吸作用效果明显优于磨料管非对称型喷嘴。在高速水流靠近磨料管附近形成了2个大小几乎相同的漩涡区，该漩涡区沿着高速水流对称分布，很好解决了非对称型喷嘴内外流场的磨料浆体集中于一侧的问题。

图8 1组磨料管对称型喷嘴的磨料速度矢量Fig.8 Abrasive velocity vector of a set of symmetrical nozzles of abrasive pipes

图9示出1组磨料管对称型喷嘴在纵截面的体积分数云图，图中混合腔的高速水流，由于水速极快，很少有磨料浆体进入内部与之混合，主要是集中在高速水流的表面扩散层，并随着高速水流的表面扩散层一起流动。距离喷嘴出口40 mm处，直径为12 mm的射流核心段横截面磨料体积分数云图如图10所示。由图可知，中心高速水流内的磨料浆体体积数很小，约在0.1左右；从射流的中心区域到边缘区域，磨料的体积分数先逐渐增大再逐渐减小。

图9 1组磨料管对称型喷嘴的磨料体积分数云图（纵截面）Fig.9 Abrasive volume fraction nephogram of a set of symmetrical nozzles of abrasive pipes（longitudinal section）

图10 1组磨料管对称型喷嘴的磨料体积分数云图（横截面）Fig.10 Abrasive volume fraction nephogram of a set of symmetrical nozzles of abrasive pipes（cross section）

综上分析比较可得，在同样条件下，1组磨料管对称型喷嘴的磨料浆体混合情况是优于非对称型喷嘴的磨料浆体混合情况。但磨料浆体还有部分集中在高速水流的靠近磨料管来流侧，未能沿径向均匀分布，磨料混合情况还可继续改善。

3.3 2组磨料管对称型喷嘴

2组磨料管对称型喷嘴也是在保证磨料管道总横截面积不变的情况，用4个两两对称的磨料管道去代替非对称型喷嘴的一个总磨料管道形成的。

从图11示出的2组磨料管对称型喷嘴的水速云图可得，由于流入喷嘴混合腔内的是四股两两对称的磨料浆体，很好地抵消了对侧磨料浆体对高速水流的冲击影响，高速水流未发生偏移弯曲，高速水流的能量损失很小。

图11 2组磨料管对称型喷嘴的水速云图Fig.11 Water speed nephogram of 2 sets of symmetrical nozzles of abrasive pipes

图12～14分别示出2组磨料管对称型喷嘴混合腔的磨料速度矢量，喷嘴纵截面的磨料体积分数云图和距离喷嘴出口40 mm处、直径为12 mm的射流核心段横截面磨料体积分数云图。从图12～14可得，在高速水流周围因卷吸作用产生的漩涡区很好地把磨料浆体与高速流混合，且混合后在高速水流周围的磨料浆体浓度是大于1组磨料管对称型喷嘴混合腔内高速水流周围的磨料浆体浓度，在喷嘴纵截面和外流场射流核心横截面上的磨料分布也明显优于1组磨料管对称型喷嘴的分布。

图12 2组磨料管对称型喷嘴的磨料速度矢量Fig.12 Abrasive velocity vector of 2 sets of symmetrical nozzles of abrasive pipes

图13 2组磨料管对称型喷嘴的磨料体积分数云图（纵截面）Fig.13 Abrasive volume fraction nephogram of 2 sets of symmetrical nozzles of abrasive pipes（longitudinal section）

图14 2组磨料管对称型喷嘴的磨料体积分数云图（横截面）Fig.14 Abrasive volume fraction nephogram of 2 sets of symmetrical nozzles of abrasive pipes（cross section）

综合以上分析，2组磨料管对称型喷嘴的磨料浆体混合效果是优于1组磨料管对称型喷嘴。但在高速水流周围，靠近磨料浆体来流方向的4个位置，磨料浓度略高于其余位置浓度，混合稍有不均。

3.4 环形磨料管对称型喷嘴

环形磨料管对称型喷嘴是将单根或多根磨料管道，在保证其总截面积不变的情况下，将磨料管道设置为环形管道，磨料浆体可通过环形管道进入喷嘴混合腔与高速水流发生混合。

由于磨料管道设置为环形，磨料浆体进入混合腔后，可在高速水流周围的所有方向上都与之发生卷吸混合。磨料浆体的总流量均分到了磨料管道的所有方向上，每个方向的磨料浆体流量较第3.1节、3.2节及3.3节的喷嘴单方向上磨料流量有了大幅度减少，再加之磨料管道设置为环形对称，导致环形磨料管道流出的磨料浆体对高速水流没有造成弯曲偏移的影响，高速水流在喷嘴内流场及外流场是完全对称的，在喷嘴内部损失的能量也是本文中所述的几组喷嘴中最小的，环形磨料管对称型喷嘴内外流场的水速云图如图15所示。

图15 环形磨料管对称型喷嘴的水速云图Fig.15 Water speed nephogram of symmetrical nozzles of ring abrasive pipes

图16示出喷嘴混合腔内磨料速度矢量，从图可见，磨料浆体在高速水流周围生成了漩涡区，漩涡区沿着高速水流的对称性分布是优于文中其余喷嘴的，导致磨料浆体因卷吸作用下与高速水流混合得更加均匀。

图16 环形磨料管对称型喷嘴的磨料速度矢量Fig.16 Abrasive velocity vector of symmetrical nozzles of ring abrasive pipes

图17，18分别示出在喷嘴纵截面的磨料体积分数云图和距喷嘴出口40 mm、直径为12 mm的射流核心段横截面磨料体积分数云图，与文中其余类型喷嘴的磨料体积分数云图相比，磨料浆体在喷嘴内部和在外流场区域的混合情况都更加理想。磨料沿着射流的径向方向均匀分布，在距离射流轴心线相等的位置，磨料体积分数大小保持一致，混合情况得到了很大改善。

图17 环形磨料管对称型喷嘴的磨料体积分数云图（纵截面）Fig.17 Abrasive volume fraction nephogram of symmetrical nozzles of ring abrasive pipes（longitudinal section）

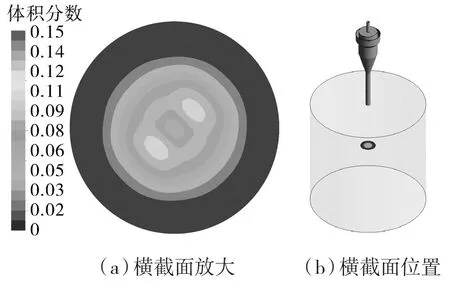
图18 环形磨料管对称型喷嘴的磨料体积分数云图（横截面）Fig.18 Abrasive volume fraction nephogram of symmetrical nozzles of ring abrasive pipes（cross section）

3.5 数据分析

选取距离各喷嘴出口40 mm处的射流核心段横截面，以截面圆心为原点，沿水平直径方向均匀选取36个样本数据点，得到各组喷嘴的磨料体积分数波动如图19所示。处理各组样本数据点，距离喷嘴出口40 mm处射流核心段截面上的磨料速度均值见表4。

图19 磨料体积分数波动Fig.19 Fluctuation of abrasive volume fraction

表4 磨料速度的均值Tab.4 Average value of abrasive speed

选取水喷嘴入口截面圆心为原点，沿喷嘴中心轴线的距离为X值，中心轴线上的水速为Y值，建立平面坐标系。各喷嘴沿中心轴线的水速如图20所示，其中X值为85 mm时，为喷嘴出口截面位置。

图20 中心轴线水速波动Fig.20 Water speed fluctuation graph about central axis

4 结论

（1）单根磨料管非对称型喷嘴虽加工和使用方便，但由于磨料浆体对高速水流的冲击碰撞影响大，高速水流发生弯曲偏移，造成水射流能量损耗较大，磨料水射流在非对称型喷嘴外流场的速度明显低于在对称性喷嘴外流场的速度；且磨料与高速水流混合不均匀，磨料集中在磨料管道侧，混合效果不理想。

（2）磨料管道对称型喷嘴明显提高了磨料与高速水流的混合均匀性和磨料水射流在外流场的速度；随着磨料管道数目的增加，磨料浆体对高速水流造成的影响越小，磨料水射流在外流场的速度越大，且磨料沿着射流的径向方向分布也越均匀。