超声振动辅助磨削弧区的单颗磨粒切厚特征＊

张 坤，殷 振，戴晨伟，苗 情，程祺辉

（苏州科技大学 机械工程学院，江苏 苏州 215009）

磨削加工中，砂轮表面的大量磨粒与工件接触，切削形成磨屑。单颗磨粒最大未变形切屑厚度（即单颗磨粒切厚）对分析磨削过程中的磨削力、磨削温度、表面粗糙度和砂轮磨损的变化规律具有重要作用[1-4]。由于每颗磨粒的切削情况均不相同，因此单颗磨粒切厚的大小具有随机性[5]。对于工作面磨粒分布情况相对可控的特制钎焊CBN 砂轮，其单颗磨粒切厚分布特征可以在一定程度上预测磨削加工的工件表面形貌[6]。丁晨等[7]考虑了磨粒高度的非正态性，利用Johnson 变换及其反变换重构了单层钎焊CBN 砂轮的工作面形貌，并分析了磨削加工参数对单颗磨粒切厚特征的影响。田霖等[8]研究了砂轮线速度对难加工材料成屑的影响规律，并建立了临界成屑厚度的计算公式，定量分析了“速度效应”对临界成屑厚度的影响。

与传统磨削相比，超声振动辅助磨削改变了材料的微观去除过程，具有降低磨削力和磨削温度[9]，减少砂轮磨损[10]，提高表面质量[11]等优点。CHEN 等[12]研究了不同断裂机制下Cf/SiC 复合材料的去除机理，结果表明：在相同磨削参数下，超声振动辅助磨削所得的单颗磨粒切厚更小，表面质量更好，且表面质量的改善效果随着超声振幅的增大而提升。JAIN 等[13]假设磨粒具有相同的尺寸和出刃高度，建立了旋转超声辅助磨削的单颗磨粒切厚模型，相比传统磨削，超声辅助磨削的切厚更小、切屑更长。ZHANG 等[5]建立了超声振动辅助磨削下硬脆材料发生脆延性转变的临界切厚模型，并研究了单颗磨粒切厚对磨削比能的影响。ZHOU等[14]结合仿真与试验，发现超声振动辅助磨削的平均微变形切厚更小、更均匀。综上所述，对超声振动辅助磨削的单颗磨粒切厚研究大多是在假设单颗磨粒切厚为单一均值的基础上进行的，缺少对实际相邻磨粒互相干涉引起材料微观去除时的切厚变化的详细分析。

因此，考虑砂轮工作面形貌的复杂性，兼顾磨粒出刃高度及相邻磨粒间距随机性的影响，通过实际测量多层金属结合剂金刚石砂轮的磨粒出刃高度和相邻磨粒间距，结合超声振动参数和磨削加工参数，利用MATLAB软件计算超声振动辅助磨削下的接触弧区的单颗磨粒切厚，分析各加工参数对单颗磨粒切厚特征的影响规律。

1 超声振动辅助磨削的单颗磨粒切厚模型

1.1 切屑微观形成过程

图1为磨削弧区切屑微观形成过程，其中：ap为磨削深度，vw为工件进给速度，vs为砂轮线速度，agmax为传统磨削下的单颗磨粒切厚，augmax为超声振动辅助磨削下的单颗磨粒切厚，A为超声振幅，f为超声振动频率。传统磨削中，单颗磨粒切厚由沿着砂轮旋转方向的相邻2 颗有效磨粒的最高点（即切刃顶点）决定，2 个切刃顶点的运动轨迹相互干涉形成切屑，如图1a 所示。上弧线（实线）为磨粒1 在接触区的运动轨迹，下弧线（虚线）为磨粒2 的运动轨迹。但是，在超声振动辅助磨削时，高频振动使相邻2 颗磨粒的运动轨迹在接触弧区往复交叉，形成多段切屑，如图1b 所示。因此，超声振动辅助磨削的单颗磨粒切厚是相邻磨粒参数、超声振动参数及磨削加工参数三者共同作用的结果。

图1 磨削弧区切屑微观形成过程Fig.1 Chip formation process in grinding arc zone

1.2 砂轮工作面相邻磨粒参数

选用直径为20 mm 的青铜结合剂多层金刚石砂轮，磨粒粒度代号为80/100，如图2所示。将砂轮沿周向均分为8 个区域，采用VHX5000 超景深显微镜在每个区域内沿砂轮轴向测量50 组相邻磨粒的周向磨粒间距（图2a）、25 颗磨粒的出刃高度（图2b），共计获得400 组磨粒间距和200 颗磨粒的出刃高度数据，其频率分布直方图分别如图2c 和图2d 所示，平均值分别为0.412 mm 和53 μm。

图2 多层金刚石砂轮工作面磨粒参数测量过程及结果Fig.2 Measurement process and results of abrasive parameters of multi-layer diamond grinding wheel working face

1.3 单颗磨粒切厚计算方法及加工参数

根据图1b 所示xOy坐标系，建立超声振动辅助磨削的单颗磨粒运动轨迹方程（见式（1）），获取磨粒在各个位置的坐标。

式中：t为运动时间；Ax，Ay分别为x，y方向的超声振幅；ω为超声振动角频率；φx，φy分别表示x，y方向的超声振动相位；ds为磨粒顶点的回转直径，且ds=db+h。其中：db为基体直径，h为磨粒出刃高度。

砂轮转动1 周，将磨粒顶点坐标满足x≤ 0 且y≤ap的轨迹区域定义为成屑时磨粒与工件的完整接触弧区。为求解完整接触弧区内相邻2 颗磨粒运动轨迹干涉后产生的有效切厚，采用等分线划分的方法将接触弧区划分为若干等份，如图3a 所示。

图3 超声振动辅助磨削的单颗磨粒切厚特征计算方法Fig.3 Calculation method of undeformed chip thickness characteristics in ultrasonic vibration-assisted grinding

设磨粒2 在磨粒1 之后接触工件。式（2）表示磨粒在等分线k处的x坐标。首先，根据式（2）计算磨粒1，2 运动到等分线k处的时间tk1，tk2；再根据式（3）计算相应的y坐标yk1，yk2；根据式（4）计算磨粒2 在等分线k处的磨削角θk2。则磨粒2 在等分线k处对应的切厚值可表示为2 颗磨粒的y坐标差值与磨粒2 在此处磨削角的乘积，即aug,k=(yk1-yk2)·θk2。

式中：x0为等分线步长，tk是磨粒从原点运动到等分线k的时间，yk指磨粒在等分线k处的y坐标。

磨粒与工件完整接触弧区的典型切厚特征计算结果如图3b 所示。定义1～n各等分线处的切厚计算结果为切厚值，定义切厚值≥0 的曲线部分与x轴所围区域为有效切厚区（该区域为磨屑产生区，有效切厚区面积表示磨屑在xOy面内的截面积，反映了材料去除率的高低），定义每个有效切厚区的最大值为局部最大切厚。数值计算时，从-Lw（Lw为工件长度）到0 依次求切厚值，所以局部最大切厚1 即为初始最大切厚。完整接触弧区的最大切厚值定义为单颗磨粒切厚，如图3b中的局部最大切厚2 即为单颗磨粒切厚。图3b 的条件参数为：磨粒间距Lg为0.412 mm，相邻磨粒高度差hd为66 μm，振动方向为x方向，超声振幅Ax为6 μm，超声振动频率fx为25 kHz，砂轮转速n为6 000 r/min，工件进给速度vw为200 mm/min，磨削深度ap为15 μm。

基于上述计算方法，将工件长度等分为1 000 份，在x，y方向施加超声振动，采用MATLAB 进行数值计算，分析相邻磨粒参数、超声振动参数、磨削加工参数对单颗磨粒切厚特征的影响，加工参数见表1。

表1 加工参数Tab.1 Processing parameters

2 结果与讨论

2.1 相邻磨粒参数的影响

沿x方向施加振幅Ax=6 μm，频率fx=25 kHz 的超声振动，设定砂轮转速n=15 000 r/min，工件进给速度vw=200 mm/min，磨削深度ap=15 μm，分析相邻磨粒参数对单颗磨粒切厚特征的影响。

2.1.1 相邻磨粒间距

根据实测的磨粒间距数据，在0.150～0.900 mm 范围内选取6 组间距，并保持相邻磨粒高度差hd为66 μm 不变。

图4为相邻磨粒间距对单颗磨粒切厚特征的影响。从图4a 可看出：切厚值受磨粒间距大小的影响非常小，变化曲线接近重合，有效切厚区数量为1。从图4b 可看出：随着磨粒间距的增大，单颗磨粒切厚在0.200 μm附近呈现微小的线性增长趋势。这是因为，磨粒间距只影响相邻磨粒在经过接触区某等分线处的时间差，但高频超声振动与高速磨削加工使磨粒间距对该时间差的影响微乎其微。

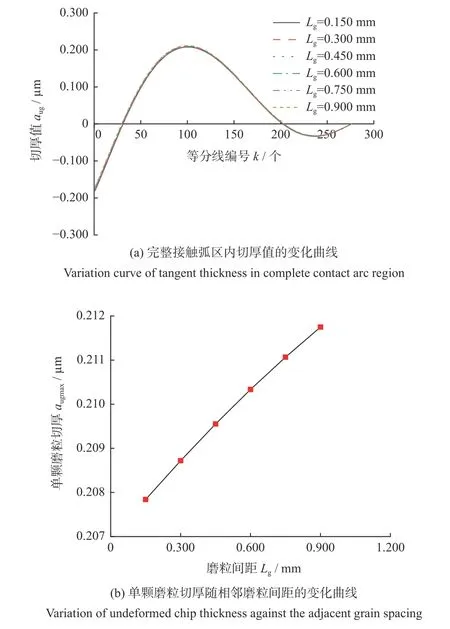
图4 相邻磨粒间距对单颗磨粒切厚特征的影响Fig.4 Influence of adjacent grain spacing on undeformed chip thickness characteristic

2.1.2 相邻磨粒高度差

设定相邻磨粒间距为实测平均值0.412 mm，并且取磨粒1 的出刃高度为27 μm，且保持不变，磨粒2 的出刃高度依次为38 μm，49 μm，60 μm，71 μm，82 μm，93 μm，分析完整接触弧区内的相邻磨粒高度差hd对单颗磨粒切厚特征的影响，如图5所示。从图5可看出：随着相邻磨粒高度差的增大，有效切厚区数量均为1，单颗磨粒切厚呈线性增大的趋势，但增幅较小。这是因为，磨粒高度差的增大使相邻磨粒在接触区某等分线处的轨迹高度差正比例增大；某等分线处的轨迹时间差受砂轮转速和超声振动影响很大。轨迹高度差和轨迹时间差均影响相邻磨粒轨迹的变化幅度，但磨粒高度差的影响程度远低于砂轮转速和超声振动的影响程度。

图5 相邻磨粒高度差对单颗磨粒切厚特征的影响Fig.5 Influence of the difference of adjacent grain heights on undeformed chip thickness characteristic

2.2 超声振动参数的影响

设定相邻磨粒间距Lg为0.412 mm，磨粒1 的出刃高度为27 μm，磨粒2 的出刃高度为93 μm，取砂轮转速n=15 000 r/min，工件进给速度vw=200 mm/min，磨削深度ap=15 μm，分析超声振动参数对单颗磨粒切厚特征的影响。

2.2.1 超声振动方向

设定超声振幅A=6 μm，超声振动频率f=25 kHz，且保持不变，分别施加x方向和y方向的超声振动及无超声振动，完整接触弧区内的切厚值的计算结果如图6所示。根据图3b 的定义，模拟图6的结果，再结合图6可得出：与x方向的超声振动相比，y方向的超声振动的切厚值、单颗磨粒切厚、有效切厚区大幅增大，切厚值个数减少；没有超声振动的情况下，切厚值非常小。这是因为，y方向的超声振动对磨粒运动轨迹在y方向的幅度变化影响很大，但缺少x方向的超声振动对有效接触弧区长度的延伸作用，所以y方向超声振动产生的切厚值个数减少，而无超声振动缺少x、y方向的超声振动的影响。

图6 超声振动方向对单颗磨粒切厚特征的影响Fig.6 Influence of ultrasonic vibration direction on undeformed chip thickness characteristic

2.2.2 超声振幅

设定x方向的超声振动频率为fx=25 kHz，且保持不变，超声振幅依次取0，2 μm，4 μm，6 μm，8 μm，10 μm，12 μm，完整接触弧区内单颗磨粒切厚特征随超声振幅的变化情况如图7所示。从图7可看出：超声振幅为0 时，接触弧区内的未变形切屑呈现典型的楔形形态。当超声振幅增大时，切厚值的数量均为1，切厚值、有效切厚区面积的变化幅度与超声振幅成正相关，单颗磨粒切厚随超声振幅的增大呈明显的线性增大趋势。这是因为，较大的超声振幅增大了相邻磨粒运动轨迹在接触弧区内的干涉程度，延长了等分线处相邻磨粒运动轨迹的时间差，相邻磨粒轨迹变化幅度较大。

图7 超声振幅对单颗磨粒切厚特征的影响Fig.7 Influence of ultrasonic vibration amplitude on undeformed chip thickness characteristic

2.2.3 超声振动频率

设定x方向超声振幅为Ax=6 μm，且保持不变，逐渐增大超声振动频率，单颗磨粒切厚的变化情况如图8所示。从图8可以看出：超声振动频率较小时，局部最大切厚数量为1，且保持不变，单颗磨粒切厚、有效切厚区随超声振动频率的增大而减小。当超声振动频率达到35 kHz 时，局部最大切厚数量增加到2，单颗磨粒切厚、有效切厚区呈增大趋势。同时，初始最大切厚始终随超声振动频率的增大而减小。这主要是因为，当砂轮转速和工件进给速度不变时，即两者相对运动一定，超声振动频率的增大使完整接触弧区内磨粒运动轨迹的变化次数增多，单颗磨粒切厚、有效切厚区发生阶段性起伏。同时，振动频率增大使相邻磨粒运动轨迹在干涉初期发生区域收缩，造成第1 个有效切厚区（即初始最大切厚）变小。

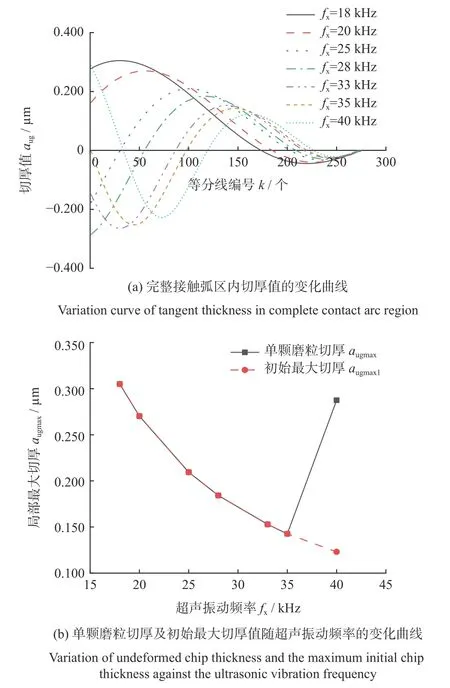
图8 超声振动频率对单颗磨粒切厚特征的影响Fig.8 Influence of ultrasonic vibration frequency on undeformed chip thickness characteristic

2.3 磨削加工参数的影响

沿x方向施加振幅Ax=6 μm，频率fx=25 kHz 的超声振动，设定相邻磨粒间距Lg为0.412 mm，磨粒1 的出刃高度为27 μm，磨粒2 的出刃高度为93 μm，分析磨削加工参数对单颗磨粒切厚特征的影响。

2.3.1 砂轮转速

设定工件进给速度vw=200 mm/min，磨削深度ap=15 μm，且保持不变，均匀增大砂轮转速，完整接触弧区内单颗磨粒切厚的变化规律如图9所示。从图9可看出：当砂轮转速小于10 700 r/min 时，存在2 个有效切厚区；当砂轮转速超过10 700 r/min 时，有效切厚区数量由2 个减为1 个；当砂轮转速增大至16 800 r/min 时，第1 个有效切厚区完全处于接触弧区内。当有效切厚区数量相同时，砂轮转速越大，单颗磨粒切厚和有效切厚区面积越大，即材料去除率越高。此外，初始最大切厚随砂轮转速的增大呈线性增大的趋势。这是因为，随着砂轮转速的增大，磨粒在接触区弧内划过的速度变大，切厚值变化曲线的起伏次数减少，使得有效切厚区的数量减少。同时，超声振动速度与磨粒运动速度的比值减小，使得超声振幅对切厚值的影响更加显著，从而增大了磨粒运动轨迹变化幅度。

图9 砂轮转速对单颗磨粒切厚特征的影响Fig.9 Effect of wheel rotational speed on undeformed chip thickness characteristic

2.3.2 进给速度

设定砂轮转速n=15 000 r/min，磨削深度ap=15 μm，且保持不变，分析不同进给速度下的单颗磨粒切厚变化情况如图10所示。从图10可看出：工件进给速度对切厚值、单颗磨粒切厚、有效切厚区的影响很小，不同进给速度下的切厚值曲线几乎重合，且有效切厚区数量均为1。随着进给速度的增大，单颗磨粒切厚呈线性增大的趋势，但稳定在0.200 μm 附近。这是因为，与砂轮转速、超声振动频率相比，工件进给速度对接触弧区内的磨粒运动轨迹的影响非常小，可近乎不计。

图10 进给速度对单颗磨粒切厚特征的影响Fig.10 Influence of workpiece infeed speed on undeformed chip thickness characteristic

2.3.3 磨削深度

设定砂轮转速n=15 000 r/min，工件进给速度vw=200 mm/min，且保持不变，完整接触弧区内单颗磨粒切厚随磨削深度的变化如图11所示。从图11可看出：当磨削深度增大到12 μm 时，第1 个有效切厚区面积增至最大，直至磨削深度为29 μm 时，保持不变；当磨削深度小于29 μm 时，有效切厚区数量为1，且保持不变，切厚值变化幅度很小，单颗磨粒切厚基本保持在0.200 μm 处；当磨削深度大于29 μm 时，有效切厚区数量变为2，且面积增大，切厚值变化幅度、单颗磨粒切厚快速变大，但初始最大切厚仍保持在0.200 μm 附近。总体上，随着磨削深度增大，磨粒与工件完整接触弧区的长度增大，有效切厚区面积先增大，后保持不变，再增大。可以推测，若继续增大磨削深度，各切厚特征循环体现。这是因为，磨削深度的改变仅使相邻磨粒运动轨迹在所建坐标内沿y方向整体平移，不影响其相对位置，但有效接触弧区的长度会随磨削深度的增大而增大，从而影响相邻磨粒运动轨迹干涉的长度，造成切厚值、有效切厚区面积、单颗磨粒切厚变大，出现切厚值变化曲线“偏移”现象。

图11 磨削深度对单颗磨粒切厚特征的影响Fig.11 Effect of the depth of cut on undeformed chip thickness characteristic

3 结论

（1）建立周向相邻2 颗磨粒运动轨迹干涉形成切屑的运动轨迹方程，并采用等分线划分方法计算求解切厚值，分析了完整接触弧区单颗磨粒切厚的典型特征。

（2）相邻磨粒间距仅影响完整接触弧区内磨粒运动轨迹的时间差，对单颗磨粒切厚无明显影响。随着相邻磨粒高度差的增大，单颗磨粒切厚呈线性增大的趋势，但增幅较小。

（3）超声振动方向与磨削速度方向接近垂直时，单颗磨粒切厚特征变化显著；二者方向接近平行时，无明显变化。单颗磨粒切厚随超声振幅的增大而线性增大，初始最大切厚随超声振动频率的增大而减小。

（4）砂轮转速的变化对有效切厚区数量和单颗磨粒切厚有较大影响，当砂轮转速低于10 700 r/min 时，存在2 个有效切厚区；当砂轮转速超过10 700 r/min 时，有效切厚区数量为1，且在有效切厚区数量相同时，单颗磨粒切厚随砂轮转速的增大而增大；与砂轮转速、超声振动频率相比，工件进给速度对接触弧区内的磨粒运动轨迹的影响非常小，以致单颗磨粒切厚特征变化较小；磨削深度影响有效接触弧区长度，对切厚值及有效切厚区影响较大。