不同加载作用下砂轮片破裂失效的有限元分析
张 维 , 颜 丰 , 周义淞
(无损检测技术教育部重点实验室(南昌航空大学),南昌 330063)
0 引言
砂轮作为磨削加工中不可或缺的一部分,是机械加工、汽车、航天等领域最常用的磨削工具[1]。在高速旋转时砂轮若破裂发生失效,其碎片因惯性作用四处飞溅,可能危及人员的生命安全[2-3],企业工人在磨削机加零件时,作业砂轮机中左侧规格为350 mm×40 mm×75 mm的砂轮突然崩裂飞出,飞出的砂轮碎片击中了作业工人,导致发生严重的工伤事故,经医学司法鉴定该事故造成工人3级伤残。目前,国内外学者针对砂轮的实验测试研究已开展了大量研究工作,如郭晔恬[4]使用树脂结合剂金刚石V形砂轮磨削碳化硅菲涅尔微结构表面,研究了砂轮磨损的实验特性,分析了砂轮磨损的损伤形式。钟彦征等[5]测试了砂轮片的动态抗弯强度。李玉秀等[6]建立了砂轮的二维有限元模型计算了砂轮在工作模态中离心力变化规律。陈建毅等[7]对砂轮在空转情况下只受到离心力的作用进行了应力和应变的分析。然而上述研究大多针对砂轮的磨损状态和评定砂轮的耐用度和磨削特性等,而对砂轮进行断裂分析的研究报道仍少见,文献[8]通过现场的检测和分析,砂轮破裂的主要原因是砂轮使用线速度过大,即砂轮机所用电动机提供的转速超过砂轮的规定转速[8]。此外,发现失效砂轮机左侧砂轮的安装轴端螺纹旋向与砂轮旋转方向相同,且砂轮轴端螺母安装未加缓冲垫片,这不符合JB/T 3770—2017《落地砂轮机》的技术要求。
鉴于应力的不可见性以及检测不便,有限元法(Finite Element Analysis,简称为 FEA)可实际的物理问题和物理场(几何结构或者是荷载情况)进行模拟分析[9-12]。本研究建立砂轮在不同工作环境下受到的力分析模型,通过模拟计算出来的砂轮应力、应变、位移的分布和大小,研究砂轮在何种力的作用下容易发生破裂,研究结果对砂轮的失效分析具有工程指导意义。
1 砂轮的有限元模型
砂轮尺寸与事故砂轮相同,内径为37.5 mm,外径为175 mm,厚度为40 mm,采用金刚石磨料,使用树脂结合剂,砂轮材料弹性模量为1 050 GPa,泊松比为0.07,密度为3.52×103kg/m3,其材料属性见表1。

表1 砂轮的材料属性Table 1 Material properties of grinding wheel
该砂轮模型采用ANSYS三维结构分析中最常用的Solid185单元。Solid185单元是一个六面体的三维实体单元,且拥有8个节点来定义三维实体结构,每个节点都有3个沿X、Y、Z方向的自由度[13]。利用软件采用自顶向下的建模方式生成圆环形状的砂轮实体模型,其内径为37.5 mm,外径为175 mm,厚度为40 mm,如图1所示。
将映射网格划分法和体扫掠网格划分法相结合对砂轮进行网格划分,定义砂轮扫掠的单元格大小为0.002。先对厚度方向的网格划分,选中Z向的所有线段划分为4个单元。然后选择映射划分,完成整个砂轮网格的划分。计算发现,有限元网格的单元数为152 352,网格结点数为193 200。
该砂轮是安装在砂轮机或角磨机的主轴上旋转工作的,所以其受到的约束是来自于内径的周向和轴向约束,而径向自由,即UY=0,UZ=0。
图1 砂轮的有限元模型Fig.1 Finite element model of grinding wheel
建立实体模型后,根据砂轮在工作中实际受力情况,在有限元模型上施加相应的载荷。砂轮在工作时受到了一个较大的离心力,对砂轮施加离心力只要定义一个绕Z轴旋转的角速度即可[14]。磨削力是磨削过程中产生的切削力和摩擦力的总和,可以分解为3个互相垂直的分力,即沿径向的法向磨削力Fn、沿切向的切向磨削力Ft以及沿轴向的轴向磨削力Fa。在砂轮工作时,一般其轴向磨削力Fa非常小,可以忽略不计,但砂轮在特殊情况下受到了端面力,那轴向磨削力Fa将会对砂轮的应力和变形产生较大的影响。本研究使用的砂轮是砂轮切割机用于直线切割工件,可以参考文献[15]提出来的磨削力公式。砂轮的实体模型建立完成后,通过对砂轮施加不同载荷,对在不同工作状态下的砂轮的应力位移进行模拟和分析,研究砂轮的应力和变形随着砂轮承受不同的力而变化的规律,以及砂轮在不同作用力下的应力位移分布情况和不同作用力对砂轮产生的影响,以此来对砂轮的失效分析和高速旋转时的破裂提供参考依据和理论基础。
2 砂轮的有限元分析
2.1 空转状态下仅受离心力
砂轮的回转强度是衡量砂轮质量和安全性的一个重要指标之一,针对砂轮在空转情况下只受到离心力的作用,实际上是和回转试验一样,分析离心力对砂轮失效的影响程度。将离心力以角速度的方式加载到砂轮的有限元模型上,然后进行求解。图2是砂轮在线速度为80 m/s的空转工况下仅受离心力的变形图、应力分布图。由砂轮的变形图和合位移图可以得出,砂轮的在离心力的作用下会发生变形,而且是沿着砂轮的径向有向外扩张的趋势,随着半径的逐渐增大,砂轮变形量就越明显。
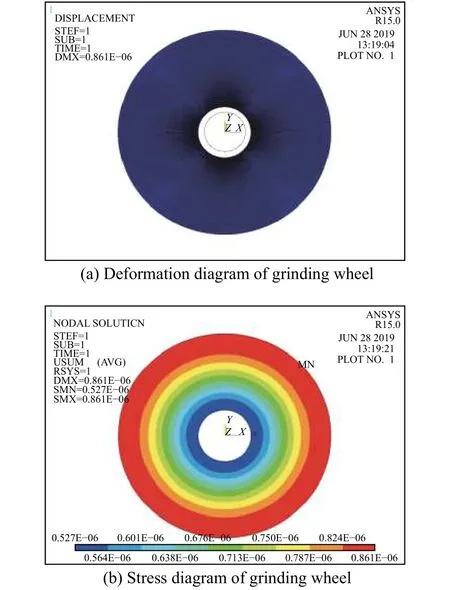
图2 砂轮仅受离心力的有限元分析Fig.2 Finite element analysis of grinding wheel only subjected to centrifugal force
图3a~图3c分别表示砂轮的径向、切向和等效的应力图。图4为砂轮受离心力作用下应力沿半径方向的变化曲线。由砂轮的应力图可知:径向应力在外圆周最小,在内孔也很小,而在内孔和外圆周之间某点达到最大值;切向应力在外圆周最小,在内孔处最大,而且随着半径的减小而增大;等效应力分布和切向应力分布图类似,因为相对来说切向应力远远大于径向应力。通过对砂轮空转情况下的有限元分析,可得对砂轮产生影响的主要是切向应力,在分析砂轮失效时应该主要考虑切向应力对其产生的影响和破坏。此外,为了研究和分析砂轮的旋转速度对砂轮的影响,对砂轮进行线速度为90 m/s的实验,实验情况与80 m/s线速度的基本一致,主要是切向应力对砂轮产生影响,如图3d所示。因此,随着转速的提高,砂轮受到的应力变大,砂轮承受的切向应力也变大,砂轮受到破坏的趋势也就越大。
2.2 工作时受离心力、磨削力
将砂轮工作参数代入理论公式,计算出切向磨削力Ft和径向磨削力Fn,并加载到砂轮模型上,然后进行求解,结果如图5所示。砂轮在工作时受到磨削力作用之后,其变形和空转时的变形基本一致,但是在受到磨削力的那个部位有更小的变形,其原因是磨削力作用于砂轮时,在径向其方向与离心力的方向相反,磨削力使砂轮有沿着半径往内径方向变形的趋势。
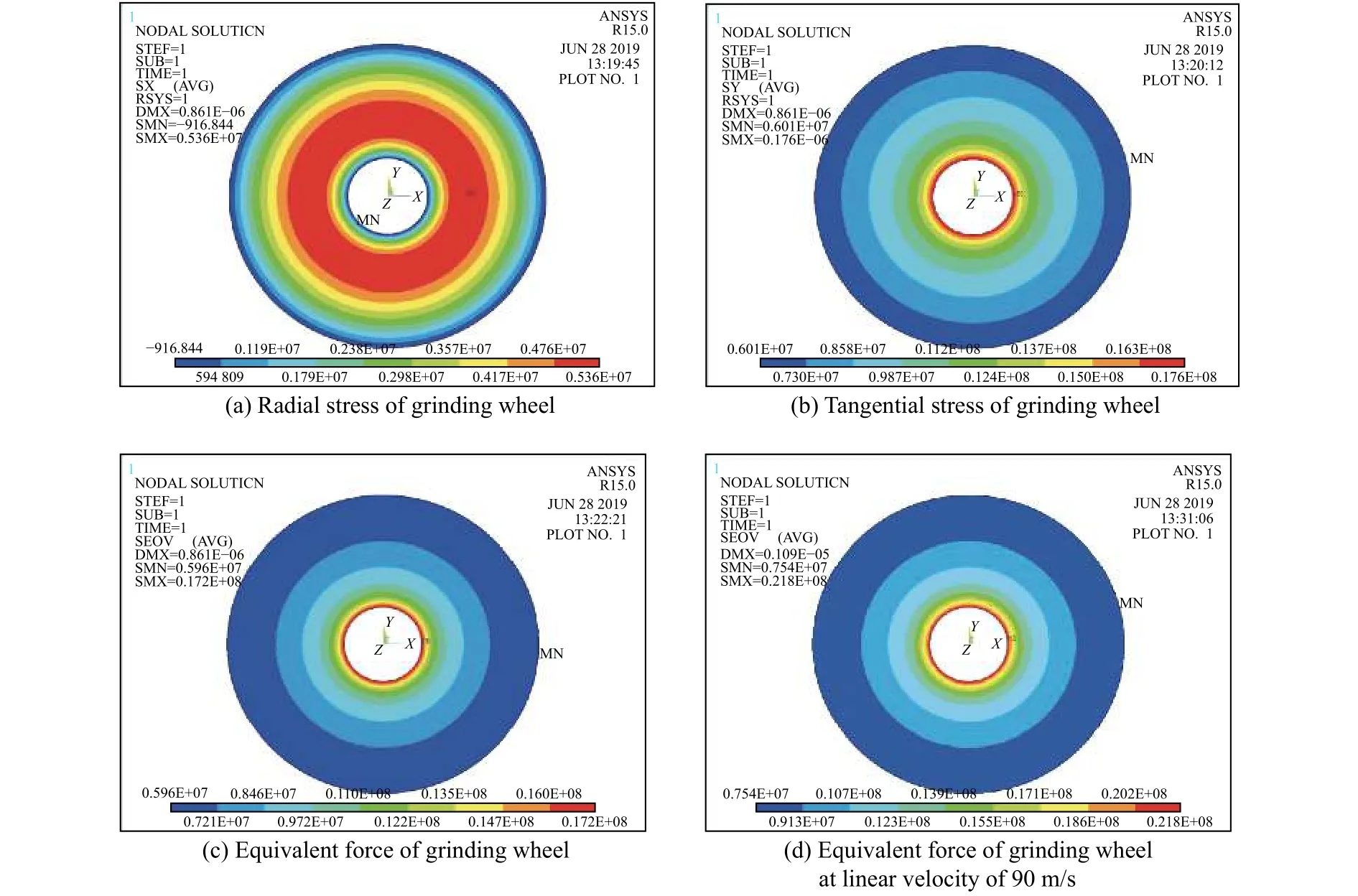
图3 不同条件下砂轮的应力分布Fig.3 Stress distribution of grinding wheel under different conditions
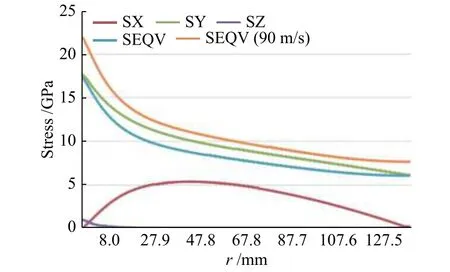
图4 砂轮仅受离心力的应力变化Fig.4 Stress change of grinding wheel under centrifugal force only
图6a~图6c分别为受到磨削力砂轮的径向、切向和等效的应力图。图7为砂轮受离心力和磨削力作用下应力沿半径方向的变化曲线。砂轮在受到磨削力的部位,受到一个切向磨削力,一个反向的径向磨削力,径向磨削力指向砂轮内孔,作用在砂轮外圆周上,因为受力面积小,所以产生一个很大的反向应力,砂轮的最小反向径向应力就在这个位置,而其他部位和砂轮空转时基本相同,最大应力值在内孔和外圆周之间某点;砂轮切向应力的最小值在施加磨削力的部位,其他部位和砂轮空转时基本相同,切向应力最大值在砂轮的内孔处;因为离心力远大于磨削力,所以工作时受到磨削力砂轮的等效应力分布和受到磨削力砂轮的切向应力分布和空转时砂轮的等效应力分布所差甚微。此外,对砂轮进行线速度为90 m/s的实验,实验情况与80 m/s线速度的基本一致,砂轮受到磨削力时的等效应力和空转时的等效应力分布基本相同,如图6d所示。由此可以表明在磨削过程中磨削力对砂轮的影响远小于离心力对砂轮的影响。
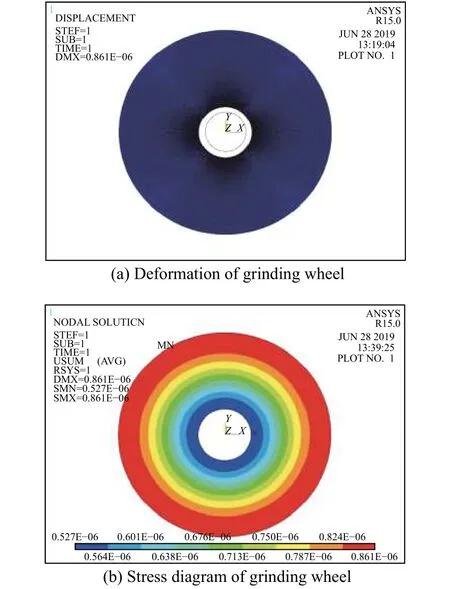
图5 砂轮受到切向和径向磨削力的变形和应力分布Fig.5 Deformation and combined displacement distribution of grinding wheel subjected to grinding force
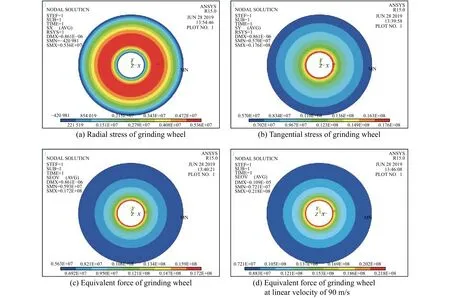
图6 磨削力加载条件下砂轮的变形和应力分布Fig.6 Stress distribution of grinding wheel subjected to grinding force
2.3 工作时受离心力、磨削力、端面力

图7 砂轮受离心力和磨削力下的应力变化Fig.7 Stress change of grinding wheel under centrifugal force and grinding force
在实际的正常切削过程中,砂轮的端面有时候会不可避免地受到工件的压力,甚至直接使用砂轮的端面进行磨削加工,由于砂轮的轴向强度很小,在这种情况下很有可能发生破裂,导致安全事故发生。将砂轮所受端面力加载到之前建立好的砂轮实体模型上,进行有限元分析求解,结果如图8所示。由图可以看出,砂轮在受端面力影响后,其轴向变形变大,而且受力一侧的变形大于另一侧,砂轮的合位移图像和轴向位移图像基本一致,说明砂轮的轴向受力占主导,大于其他2个方向也就是径向和切向的变形。所以虽然砂轮只是受到了一个小小的端面力,但是其变形量却大于正常情况下的变形量,说明端面力会对砂轮受力之后产生的变形有很大影响,是砂轮在使用时失效的一个重要影响因素。
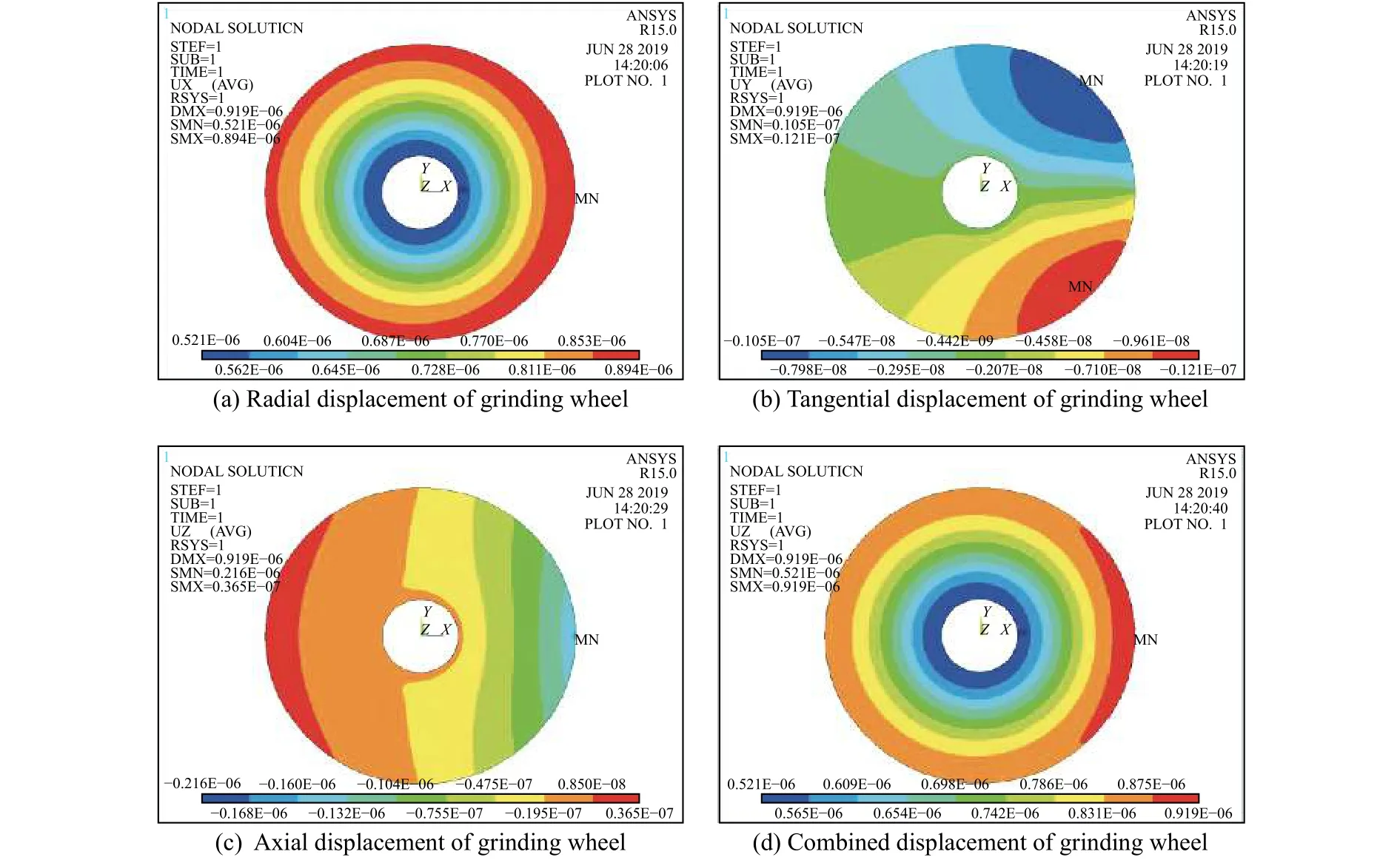
图8 砂轮正常切削过程中受端面力作用的应力分布Fig.8 Stress distribution of grinding wheel subjected to end force in normal cutting process
图9为砂轮受离心力、磨削力和端面力作用下应力沿半径方向的变化曲线。砂轮在受到端面力的作用后,砂轮的最大等效应力在受力一侧的内孔处,最小等效应力在受到端面力的部位,砂轮的等效应力分布和切向应力分布所差甚微,与上一节实验结果相比,所以虽然砂轮只是受到了一个小小的端面力,但是最大等效应力却迅速增加,如图10所示。由此可以说明,端面力对砂轮工作时的应力分布影响很大,是砂轮在工作使用时失效的一个重要影响因素。
2.4 结果分析
图11为砂轮受不同加载作用下的合位移和等效应力沿半径方向的变化曲线。砂轮在空转状态时,若仅受离心力的作用,其径向变形量最大,而且砂轮的合位移分布图和径向位移分布图基本相同;砂轮的切向应力远大于砂轮的径向应力,砂轮的等效应力分布图和切向应力分布图基本相同;随着转速的提高,砂轮受到的离心力也不断变大,所以砂轮的等效应力也随之变大,即砂轮越可能发生破裂,破坏的趋势越大。
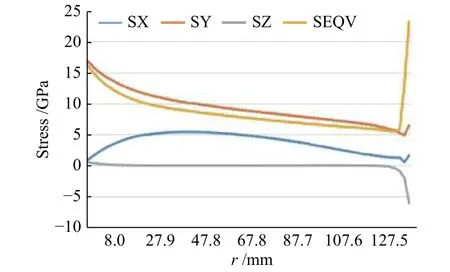
图9 砂轮受离心力、磨削力、端面力下的应力变化Fig.9 Stress change of grinding wheel under centrifugal force,grinding force and end face force

图10 砂轮端面受力下的应力分布Fig.10 Stress distribution of grinding wheel subjected to end force
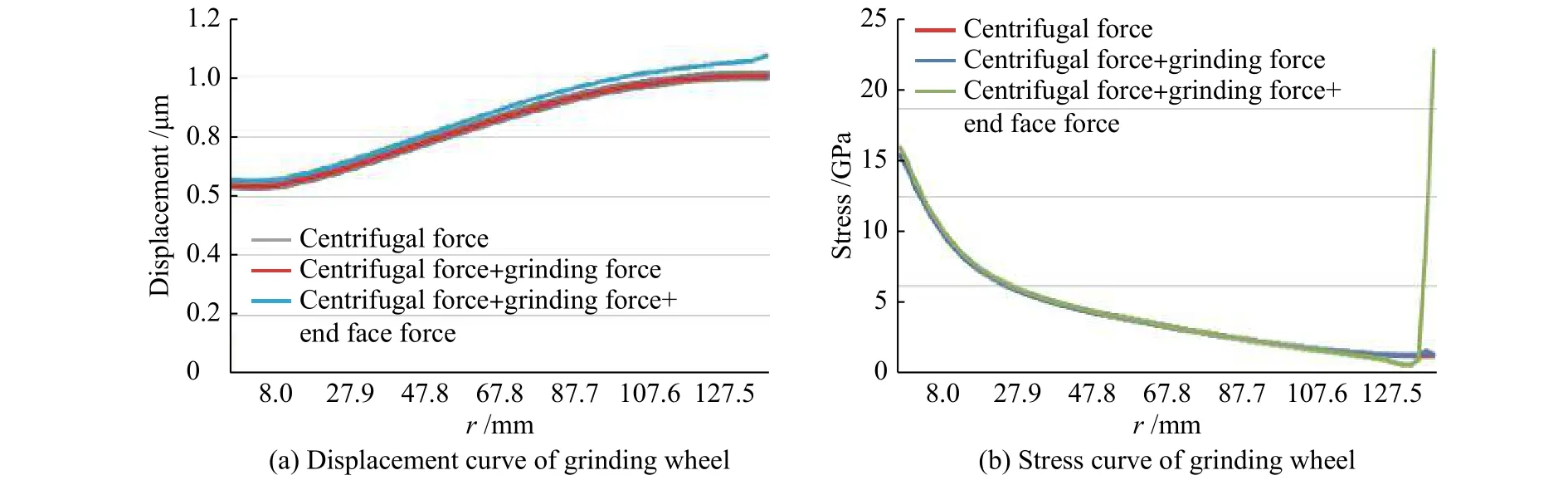
图11 砂轮受不同力下的位移、应力变化Fig.11 Displacement and stress changes of grinding wheel under different forces
砂轮在受离心力和磨削力的正常工作情况下,其应力和应变的分布情况和实验一基本相同,因而可以说明磨削力对砂轮的影响比较小。
在砂轮正常工作情况下,除了受离心力和磨削力作用外,再对砂轮施加一个端面力,砂轮的轴向位移突然增大,而且大于径向位移和切向位移,其合位移分布图和轴向位移分布图基本相同,而且砂轮在受到端面力后各向应力相对于正常情况也明显增大,最大等效应力相对于正常工作情况来说迅速增加,但是整体上还是切向应力>径向应力>轴向应力,等效应力分布图和切向应力分布图基本相同。由此可见,砂轮在受到端面力的情况下,砂轮的应力应变都发生了变化,且都增加了不少,端面力是造成砂轮在工作中失效破裂的主要原因之一。
综上所述,在离心力、磨削力、端面力这3种作用力中,对砂轮应力影响是离心力>端面力>磨削力,而对砂轮应变影响则是端面力>离心力>磨削力,而且磨削力因为有一个径向的反向分力,在分析过程中其对砂轮的应力应变还有减轻的作用,但不是很明显。造成砂轮发生破裂失效的原因有砂轮选取不正确、使用砂轮非工作平面进行磨削、磨削加工时进刀量太大、砂轮工作线速度超过最高工作速度,砂轮孔径与砂轮机主轴外径不匹配、砂轮机的卡盘安装不正确、砂轮主轴螺纹安装不当等,主要原因是转速过高离心力过大、砂轮工作时产生晃动、砂轮在磨削过程中受到了较大端面力的作用。
3 结论
1)通过对不同加载作用下的砂轮片进行有限元分析,对比分析不同力作用下砂轮的位移和应力,在可能引起砂轮片失效破坏的3种因素中,离心力对砂轮片应力的影响大于端面力的影响,端面力的影响要大于磨削力的影响;端面力对砂轮片应变的影响要大于离心力对应变的影响,离心力对应变的影响大于磨削力的影响。总体来说,离心力对砂轮片的应力应变影响最强,端面力次之,磨削力对砂轮片的影响作用很小。
2)在使用过程中,过大线速度带来的过大离心力和使用砂轮端面磨削带来的端面力是造成砂轮破裂的主要因素。可以为优选加工工艺参数,减少砂轮片磨损、改善工作条件,为砂轮片的结构参数优化和强度设计提供参考依据,同时也可以针对砂轮片薄弱位置对其进行补强加固。

