截点法测量金属平均晶粒度的不确定度评定及分析

刘 松

（航空工业金城南京机电液压工程研究中心，南京 211106）

0 引言

对材料的任何特征性能参量进行检测或测量时，尽管方法和仪器设备不断完善，其测量结果始终存在着不确定性，而这种不确定性往往使用误差来描述。然而，对于材料的许多特征参量，真值是无法知晓的，所以误差不能准确得到，在应用中往往是用近似真值来代替，而近似真值本身就具有不确定度，即误差必然存在着相当的不确定度[1]。自从国际不确定度工作组制定的《测量不确定度表示指南》（GUM）在全世界推广和执行以来，测量不确定度评定已成为当今科学界、质量技术监督部门、各类认可和认证机构关注的热点。我国JJF1059《测量不确定度评定与表示》规范发布以后，对于计量部门的校准实验室，许多计量设备和仪器已经有了较为成熟的不确定度评定与表示的研究成果。然而，对于检测实验室，理化检测结果不确定度评定与表示的研究成果还处于起步探索阶段。GB/T 27025《检测和校准实验室能力的通用要求》规定，不管是已认可或准备认可的检测或校准实验室，都必须具有应用评定测量不确定度的程序。标准明确指出：当不确定度与检测结果的有效性或应用有关，或客户的指定中有要求，或当不确定度影响到对规范限度的符合性时，检测报告中还需要包括有关不确定度的信息。中国实验室认可委员会CNAS/CL07：2011《测量不确定度的要求》也明确规定，检测实验室应有能力对每一项有数值要求的测量结果进行测量不确定度评估。因而，测量不确定度的评定和表示得到了设备仪器校准工作者的高度重视同时，也得到了从事材料检测的广大理化检验工作者的重点关注[2-7]。

1 试验条件及方法

仪器：Zeiss AXIO Scope1型金相显微镜，放大倍率偏差≤±5%；Proimaging金属金相智能分析系统软件，100倍下的数码金相图片分辨率0.452 726 μm/px。

环境条件：评定温度为20 ℃，相对湿度为57%。

测定对象：DT4A退火样品（均匀等轴晶粒）。

测定内容及方法：截点数目和平均截距。根据GB/T 6394—2017《金属平均晶粒度测量方法》标准规定的截点法，采用经检定合格的金相显微镜和金相分析软件对样品进行平均晶粒度测量，试验结果分别由3名试验人员在完全相同试验条件（相同视场、同一截线、晶界清晰）下，利用金相显微镜目镜和金相分析软件手动计数测量方式，各测量3组数据，评定样品的晶粒度形貌，如图1所示。

2 数学模型及公式

截点法测量金属平均晶粒度的数学模型为：

式中：¯为平均截距长度，μm；L为试验线长度，μm；Pi为晶界与试验线的交点数。

根据不确定度的传播规律，由y=f(x1,x2,···,xn)，则y的估计值的合成标准不确定度uc(y)按式（2）进行计算：

图1 晶粒度形貌及测量方法Fig.1 Morphology of average grain size and measuring method

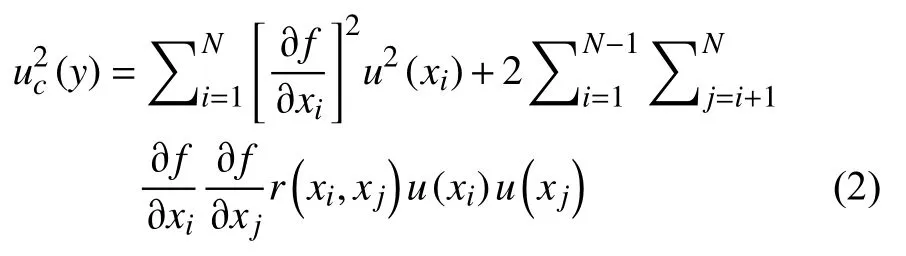
式中：y为被测量的估计值，又称输出量的估计值；xi为输入量的估计值；为被测量与有关的输入量之间的函数对于输入量的偏导数，又称灵敏系数为输入量xi的标准不确定度为输入量xi与输入量xj的相关系数。

输入量xi与输入量xj的相关系数与输入量xi和xj的协方差关系为：

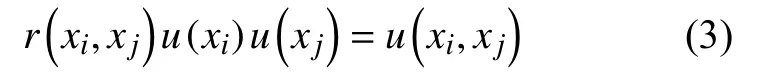
2个重复同时观测的输入量xi，xj的协方差估计值可由式（4）确定。

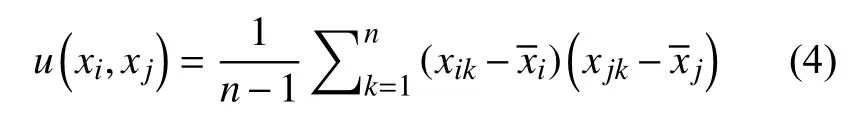
式中：xik、xjk分别是测得值；k为测量次数；、分别为第i个和第j个输入量的测量值的算术平均值。

试验线长度L是固定常数，因而2个输入量xi、xj的协方差取为灵敏系数。

3 测量不确定度评定

3.1 不确定度来源分析

截点法测量均匀等轴晶粒（DT4A材料，单相铁素体，晶界清晰，相同视场，同一截线）的平均晶粒度结果不确定度的主要来源：金相显微镜放大倍率偏差的不确定性导致应用目镜测量平均晶粒度时，试验线长度L引入的不确定度分量u11(L)；由金相显微镜标尺尺寸的不确度传递到金相分析软件手动测量平均晶粒度时，试验线长度L引入的不确定度分量u12(L)。目镜的刻度尺最小分辨刻度，导致应用目镜测量平均晶粒度时，试验线长度L引入的不确定度分量u21(L)；金相分析软件的图像分辨率，致使其手动测量平均晶粒度时，试验线长度L引入的不确定度分量u22(L)。应用目镜测量平均晶粒度时，试验人员测量晶界与试验线的交点数的结果重复性，引入的不确定度分量u11(Pi)；使用金相分析软件手动测量平均晶粒度时，试验人员测量晶界与试验线的交点数的结果重复性，引入的不确定度分量u12(Pi)。截点法的截线方式不同，导致截点个数最小分辨力对测量晶界与试验线的交点数不确定性的影响，引入的不确定度分量u2(Pi)；直线截点法引入的不确定度分量u21(Pi)，圆截点法引入的不确定度分量u22(Pi)。

3.2 不确定度评定

3.2.1 试验线长度L的标准不确定度u(L)

显微镜放大倍率偏差≤±5%，属于B类均匀分布，试验线长度L为5 000 μm。因而，金相显微镜放大倍率偏差的不确定性导致应用目镜测量平均晶粒度时，试验线长度L引入的不确定度分量为：

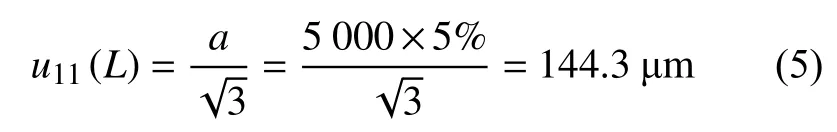
目镜的刻度尺最小刻度δ=10 μm，服从B类均匀分布。因而，目镜刻度尺分辨力导致应用目镜测量平均晶粒度时，试验线长度L引入的不确定度分量为：

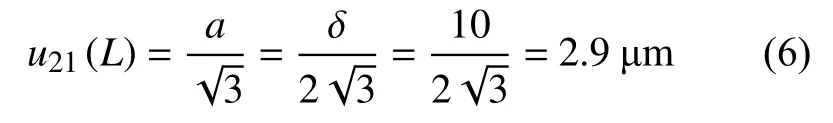
因此，应用目镜测量平均晶粒度时，试验线长度L引入的不确定度分量合成的标准不确定度为：

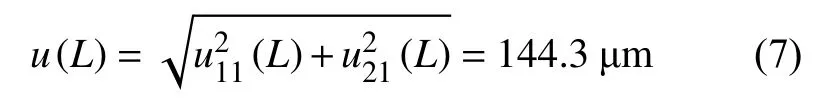
当应用金相分析软件手动测量平均晶粒度时，由标定使用的标尺的校准结果的扩展不确定度U=1.6 μm（k=2，温度 20.1 ℃）传递到金相分析软件，导致试验线长度L引入的不确定度分量为：

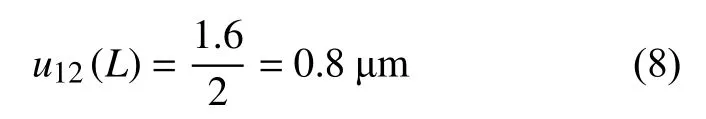
在100倍下的数码金相图像分辨率为0.452 726 μm/px。应用金相分析软件手动测量平均晶粒度时，金相分析软件的图像分辨力，导致试验线长度L引入的不确定度分量为：

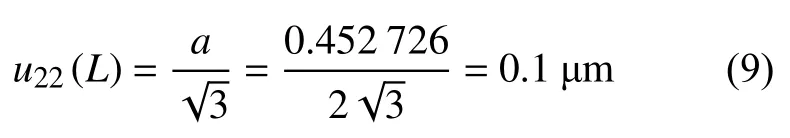
因此，应用金相分析软件手动测量平均晶粒度时，试验线长度L引入的不确定度分量合成的标准不确定度为：

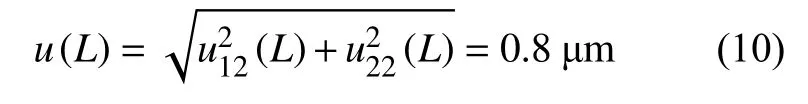
3.2.2 试验截点数Pi的标准不确定度u(Pi)

应用目镜测量平均晶粒度时，试验人员测量晶界与试验线的交点数的结果重复性，引入的不确定度分量u11按A类不确定度进行计算。表1为3名试验人员在完全相同试验条件下，分别3次应用金相显微镜目镜测量的晶界与试验线的交点数。

由表1中的数据得出标准差平均值为：

表1 应用金相显微镜目镜测量的晶界与试验线的交点数Table 1 Intersection points between grain boundary and test line measured by metallographic microscope eyepiece

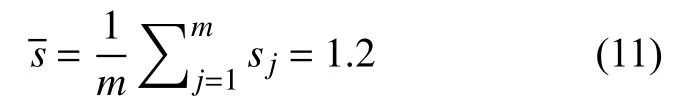
式中：j为测量人员序号；sj为样本标准差；m为参与测量的人数。

合并样本标准偏差为：

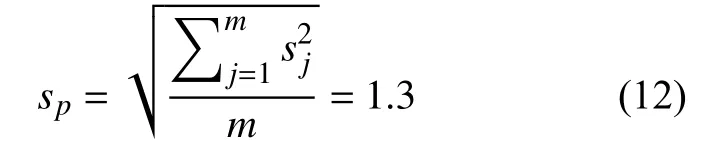
应用目镜测量截点个数的重复性所引入的不确定度分量为：

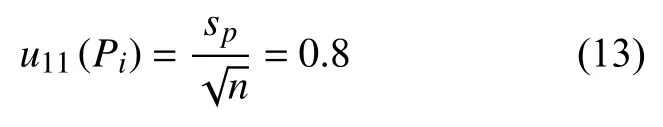
式中：n为每个测量人员的测量次数。

同时，由表1应用金相显微镜目镜测量晶界与试验线的交点数可知，L为5 000 μm，平均截点数为139.9，平均截距为35.7 μm。因此，灵敏系数CL为 0.007 1，CPi为−0.255 5。

应用金相分析软件手动测量平均晶粒度时，试验人员测量晶界与试验线的交点数的结果重复性，引入的不确定度分量u12按A类不确定度进行计算。表2为3名试验人员在完全相同试验条件下，分别3次应用金相分析软件手动测量的晶界与试验线的交点数。

表2 应用金相分析软件手动测量的晶界与试验线的交点数Table 2 The intersection points between grain boundary and test line measured by analysis software

由表2中的数据得出标准差平均值为：

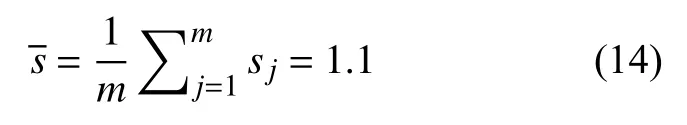
式中：j为测量人员序号；sj为样本标准差；m为参与测量的人数。

合并样本标准偏差为：

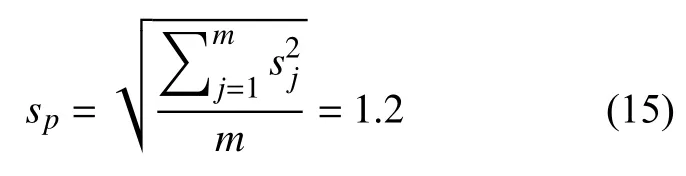
应用金相分析软件手动测量截点个数的重复性所引入的不确定度分量为：

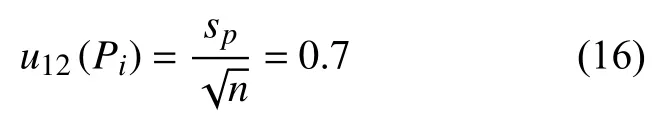
式中：n为每个测量人员的测量次数。

同时，根据表2应用金相分析软件手动测量晶界与试验线的交点数可知，L为5 000 μm，平均截点数为140.8，平均截距为35.5 μm。因此，灵敏系数CL为 0.007 1，CPi为−0.252 2。

根据GB/T 6394—2017《金属平均晶粒度测量方法》标准规定，直线截点法最小可计0.5个截点，而圆截点法最小计1.0个截点。因而不同样式截线的截点法，其最小截点的计数方式引入的不确定分量也有所不同。

采用直线截点法最小可计0.5个截点，服从B类均匀分布，引入的不确定度分量为：

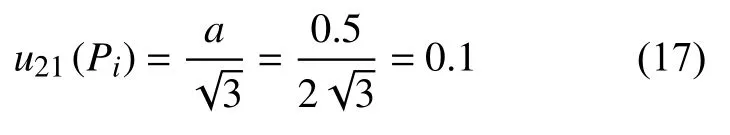
采用圆截点法最小计1.0个截点，服从B类均匀分布，引入的不确定度分量为：

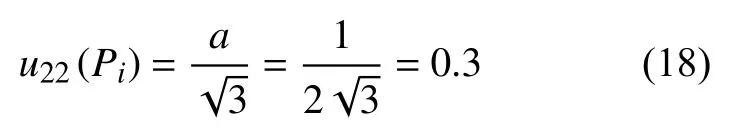
应用目镜，采用直线截点法测量平均晶粒度时，晶界与试验线的交点数Pi引入的不确定度分量合成的标准不确定度为：

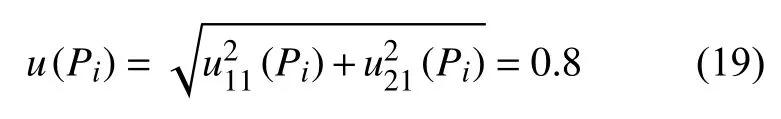
应用目镜，采用圆截点法测量平均晶粒度时，晶界与试验线的交点数Pi引入的不确定度分量合成的标准不确定度为：

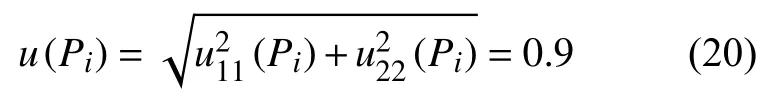
使用金相分析软件，采用直线截点法手动测量平均晶粒度时，晶界与试验线的交点数Pi引入的不确定度分量合成的标准不确定度为：

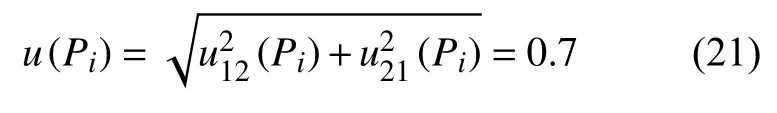
使用金相分析软件，采用圆截点法手动测量平均晶粒度时，晶界与试验线的交点数Pi引入的不确定度分量合成的标准不确定度为：

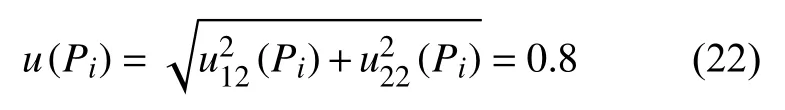
3.2.3 合成标准不确定度的评定

合成标准不确定度的评定按式（23）进行。

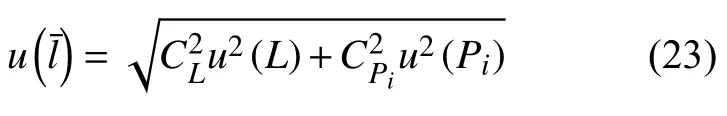
应用目镜，采用直线截点法测量平均晶粒度时，合成的标准不确定度为：

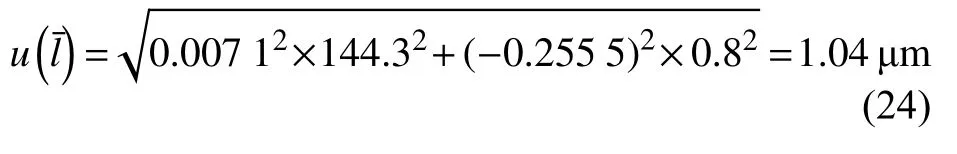
应用目镜，采用圆截点法测量平均晶粒度时，合成的标准不确定度为：

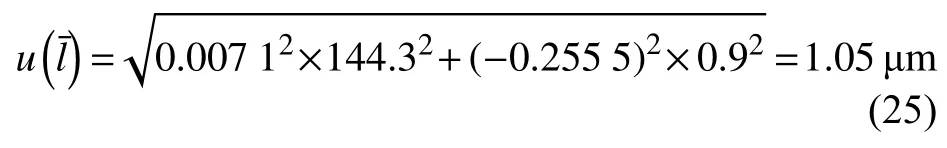
使用金相分析软件，采用直线截点法手动测量平均晶粒度时，合成的标准不确定度为：

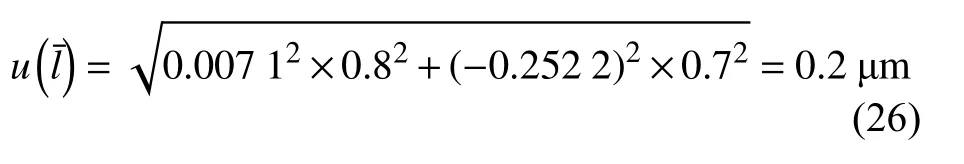
使用金相分析软件，采用圆截点法手动测量平均晶粒度时，合成的标准不确定度为：

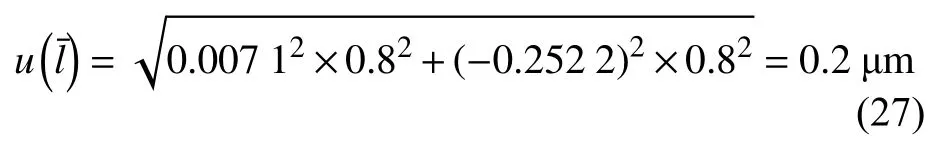
3.2.4 扩展不确定度

包含概率取P=95.45%，包含因子k=2，则扩展不确定度为：

应用目镜，采用直线截点法测量平均晶粒度的扩展不确定度为：

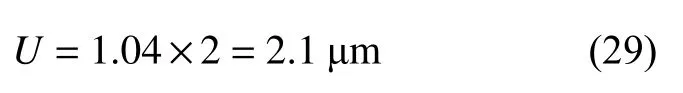
应用目镜，采用圆截点法测量平均晶粒度的扩展不确定度为：

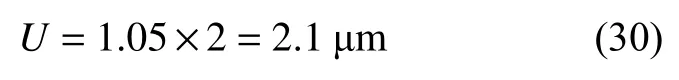
使用金相分析软件，采用直线截点法手动测量平均晶粒度的扩展不确定度为：

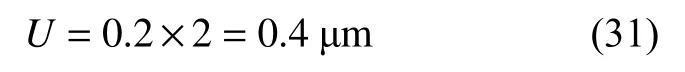
使用金相分析软件，采用圆截点法手动测量平均晶粒度的扩展不确定度为：

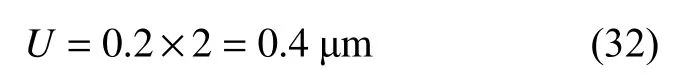
4 分析与讨论

从测量不确定度评定的结果不难看出，在其他条件均相同的情况下，应用目镜直接测量均匀等轴晶粒的平均晶粒度的不确定度要明显大于通过金相分析软件手动测量的平均晶粒度的不确定度。这是因为金相显微镜放大倍率偏差的不确定性导致应用目镜测量平均晶粒度时，试验线长度L引入的不确定度分量在各分量中的权重比较大。使用金相分析软件手动测量平均晶粒度方法，试验线长度L引入的不确定度分量要比应用目镜方法试验线长度L引入的不确定度分量小得多。因此，认为金相显微镜放大倍率偏差是影响应用目镜测量平均晶粒度结果的主要因素。应用目镜与使用金相分析软件手动测量相比，测量得到的晶界与试验线的交点数结果人员的重复性，引入的不确定分量基本相近。这可以证明，只要晶粒晶界腐刻清楚，选择合适的放大倍数，无论是应用目镜，还是金相分析软件手动测量晶界与试验线的交点数，测量的重复性引入的不确定度不会存在太大差距。由于标准规定的最小计数的要求，在相同条件，均匀等轴晶粒采用直线截点法测量平均晶粒度与采用圆截点法测量平均晶粒度相比，最小计数引入的不确定分量直线截点法的更小。尽管如此，最小计数引入的不确定分量对最终的不确定结果影响并不明显。应用目镜测量平均晶粒度结果的不确定度主要是受到试验线长度L引入的不确定度分量影响较大；而使用金相分析软件手动测量平均晶粒度结果的不确定度主要影响却是测量的晶界与试验线的交点数引入的不确定度分量。在本试验条件下，应用目镜测量平均晶粒度的扩展不确定度为2.1 μm，而使用金相分析软件手动测量平均晶粒度的扩展不确定度为0.4 μm。这说明，在其他条件均相同的情况下，使用金相分析软件手动测量平均晶粒度比应用目镜直接测量平均晶粒度更能缩小相同包含概率下结果不确定性的范围，提高了准确度。从扩展不确定度的评定结果还可以看出，直线截点法和圆截点法对最终的不确定度的评定结果不能产生太大的影响，这可能与测量的晶粒为均匀等轴晶粒有关。

5 结论

1）目镜测量平均晶粒度的平均截距值为35.7 μm，U=2.1 μm，k=2；金相分析软件测量平均晶粒度的平均截距值为 35.5 μm，U=0.4 μm，k=2。

2）金相显微镜放大倍率偏差致使试验线长度L引入的不确定度分量是应用目镜测量平均晶粒度结果不确定度的主要来源；而使用金相分析软件手动测量平均晶粒度结果测量不确定度主要来源却是由测量的晶界与试验线的交点数的不确定度分量引入的。

3）在其他条件均相同的情况下，使用金相分析软件手动测量平均晶粒度比应用目镜直接测量平均晶粒度更能缩小结果在相同包含概率下不确定性的范围，提高准确度。

4）对于均匀等轴晶粒的平均晶粒度测量，直线截点法和圆截点法对最终的不确定度的评定结果影响不大。