磨料水射流旋转切割岩石深度计算模型

刘 鑫， 许宏发， 耿汉生， 范鹏贤， 莫家权

(陆军工程大学 国防工程学院，江苏 南京 210007)

高压磨料水射流技术凭借其优异的切割性能被广泛用于材料加工切割、煤矿爆破开采等诸多方面[1-3]。借助于高压磨料水射流技术及相关装备对洞库围岩进行割缝，在洞库上方形成人工裂隙群，达到抗爆消波的工程防护目的是切实可行的。割缝深度越大，布设的人工裂隙尺寸越大，爆炸波在裂隙分界面传播绕射、反射现象增加，对爆炸波的衰减越明显。但磨料水射流对洞库围岩的切割性能仍是限制其在地下防护方面运用的主要障碍。因此，研究磨料水射流技术对洞库围岩的切割性能对在围岩中构建抗爆消波防护层具有重要意义。

宋拥政等[4]研究了花岗岩等材料经磨料射流切割后的裂隙宽度、深度等和射流压力、切割速率、靶距等参数的联系。赵永赞等[5]研究了切割时的射流参数对切割深度的影响，并对石材的切割情况进行了说明。Mohamed等[6]根据磨料微粒的侵蚀理论构建了金属的切割深度预测模型，得到射流压力是对切割深度影响最大的因素。同样，卢义玉等[7]开展了单因素试验法，用水射流技术切割砂岩，结果表明提升设备的射流压力可以有效增大切割性能。王伟等[8-9]依据试验结果得到影响磨料射流切割深度的最主要原因是横移速度。这些研究表明磨料射流中相关参数的优化改进，例如射流压力、横移速度可以显著提升磨料射流的切割能力，增大磨料射流的破岩深度。相关学者构建了不少磨料射流切割深度模型，用来评估和预测不同优化参数后的切割性能。张永将等[10]建立了单一水射流环形切割煤层的深度理论模型，并结合试验验证了割缝深度模型的正确性。王晓川等[11]利用自研磨料射流设备对不同值的泥质灰岩进行切割，建立了水平移动切割深度模型。杨林等[12]采用回归分析法构建了射流切割质量与喷射压力、磨料流量和切割速度间的经验模型。郭嘉赫等[13]采用单因素试验和正交试验法研究了靶距、射流压力、横移速度等参数对切割性能的影响，基于多元线性回归拟合得到了射流切割深度预测模型。王瑞和等[14]使用编程算法建立了射流切割深度预测模型。黄振飞等[15]基于动量守恒原理，以射流功率和冲蚀体积之间线性关系、射流动压衰减规律和Mohr-Coulomb准则为基础，研究了射流切割深度随切割时间变化的关系。

上述对于磨料射流割缝深度的研究大多数是基于喷嘴水平移动下的切割作业，很少考虑喷嘴旋转切割时的深度变化。为此，本文针对射流磨料对于材料的去除体积量，提出了基于磨料粒子去除体积量的环形射流切割深度估算模型，以实现在围岩中制作既定人工裂隙群，为洞库围岩抗爆消波人工裂隙群的构建提供理论基础。

1 单颗磨料颗粒去除材料的削切体积

1.1 磨料颗粒去除非岩石体积与磨料速度关系

单颗磨料对材料的去除(切削)作用与其冲击动能密切相关。而冲击动能的大小又与磨料质量和速度紧密相关。由动能定理可得理想状态下单个磨料微粒在射流中的冲击动能可表示为

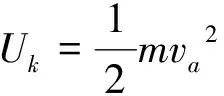
(1)

式中：Uk为磨料微粒的冲击动能，m为磨料微粒质量，va为磨料微粒速度。

而根据Mashall[16]的研究结果，磨料微粒的有效冲蚀动能取决于磨料微粒的冲击动能、磨料硬度以及被切割材料本身的硬度，即可表示为

(2)

式中：Um为有效冲蚀动能，Ha为磨料微粒的维式硬度，H为岩石的维氏硬度。

在磨料水射流垂直冲蚀材料下，磨料微粒有效断裂冲蚀动能近似等于有效冲蚀动能，即

Umc=Um

(3)

式中：Umc为垂直冲蚀下磨料微粒有效断裂冲蚀动能。

朱洪涛[17]借助脆性材料断裂力学理论，从侧向裂隙断裂面深度与材料塑性变形区之间关系构建了理想状态下(磨料垂直冲击)单个磨料微粒对于材料的体积去除量可表示为

(4)

式中：f1、f2为与材料断裂韧度有关的无量纲常数；E为材料的弹性模量；KIC为材料的断裂韧度；H为材料的维氏硬度。

1.2 磨料颗粒去除岩石体积与磨料速度关系

将磨料水射流技术拓展应用到岩石切割加工过程中，将式(1～3)代入式(4)，可得到磨料水射流垂直冲击条件下，单颗磨料对岩石的去除体积计算公式，如式(5)所示。

(5)

朱洪涛[17]采用粒径为120 μm石榴石磨料在不同射流压力、不同喷头横移速度等条件下对硅酸盐玻璃及96%Al2O3两种材料进行了磨料射流切割，对无量纲常系数进行了研究，得到磨料水射流对硅酸盐玻璃和96%Al2O3对应的无量纲常系数f1分别为0.214 20和0.038 43，f2分别为11.721 4和5.132 6，如表1所示。

表1 无量纲常系数与其断裂韧度[17]

根据表1可近似得到无量纲常系数f1、f2与断裂韧度KIC之间的经验表达式为

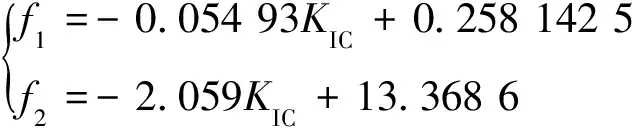
(6)

磨料为粒径0.3 mm的石榴石，维氏硬度20 GPa，密度3.95 g/cm3。假设磨料微粒为圆球状，则磨料微粒的质量可表示为

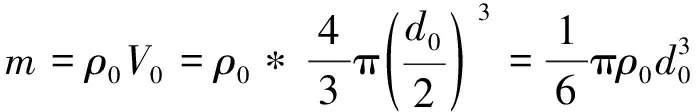
(7)

式中：ρ0为磨料微粒密度，V0为单颗磨料微粒体积，d0为磨料微粒直径。

根据李江腾等[18]研究成果，岩石断裂韧度与岩石自身抗压强度之间存在紧密联系，通过大量试验与验证得到相关经验公式为

KIC=0.026 5σc+0.001 4

(8)

式中σc为岩石的单轴抗压强度。

将不同岩石抗压强度及其相关断裂韧度以及岩石的各物理力学参数一并记录于表2。

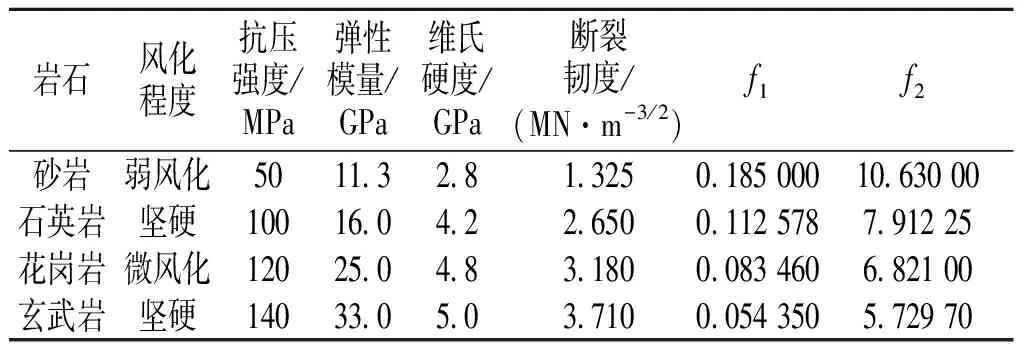
表2 岩石物理力学参数[19-20]

根据表2中各岩石条件，代入式(5)，得到磨料水射流冲击下，单颗磨料去除岩石体积与单颗磨料冲击速度之间关系，如图1所示。

图1 单颗磨料对不同岩石体积去除量

由图1可以看出：单颗磨料对于不同岩石的体积去除量是不同的，表现为相同磨料速度下，切割砂岩体积最大，切割石英岩去除体积次之，切割玄武岩体积最小；磨料切割体积与磨料速度变化呈正相关。结合表2可知，单颗磨料颗粒对不同岩石体积去除量与岩石单轴抗压强度、弹性模量及硬度呈负相关。由此可知，对于越坚硬的岩石，磨料水射流的切割能力越弱，在磨料射流切割围岩的施工运用中，人工磨料射流切割的裂隙的尺寸受围岩影响较大。

2 基于磨料颗粒去除岩石体积的环形射流切割深度估算

2.1 磨料射流切割面分析

磨料水射流对于岩石的切割深度主要受磨料流量、磨料速度、磨料种类、粒径和喷嘴尺寸及环形射流旋转速度等多方面影响。当射流工况确定时，例如，喷嘴尺寸、磨料种类一定时，磨料水射流切割深度主要取决于单位时间内作用在材料上的磨料颗粒数以及其动能[21]。

当射流磨料粒子离开喷嘴进入外流场时，此时磨料射流属于典型湍流运动，磨料受到重力Fg、压差力FP、附加质量力Fa等力的共同作用[22]，磨料运动状态及受力情况复杂，求解磨料在外流场中与喷距的变化关系困难。但已有研究表明，在射流轴向的核心射流区域，磨料颗粒在外流场中的运动速度变化为随射流距离的增大呈现先增大再减小的变化趋势[23]，故其对于材料的削切体积也随磨料速度的变化而出现先增大再减小的变化趋势。但是，观察实际射流切口，随着射流长度的增大，在近喷嘴处的一段距离内的射流从一开始直径处处相等而呈现逐渐发散的趋势，近似于锥形。如图2所示，在射流发散区边缘，磨料粒子量因射流的发散作用而减少，磨料射流整体对于材料的削切能力降低，故在射流束发散的边界处材料整体去除体积量下降。

图2 磨料水射流切割材料切口示意图

以上磨料在沿射流不同切割处的速度变化以及磨料粒子数的改变综合造成了从核心射流轴向位置随喷射距离增大而向上下射流边界发散，从而导致射流切割切口收敛的变化现象，可形象表示为切口宽度随喷射距离增大而逐渐减小。在图2中表现为长方形切割截面的面积逐渐缩小，即Sa1⟩Sa2⟩…San。

2.2 环形磨料射流切割岩石深度数学模型

如图3所示，近喷头处射流切口宽度为2a1，远端射流切口残余宽度为2a2。根据磨料射流切口形态，采用式(9)函数模拟射流上下切割边界走势，函数表达式为

图3 射流切割截面面积计算示意图

y=±a1e-λx

(9)

式中λ为切口形态指数。

假定切口宽度2a1/2a2之比为n，将切割深度R代入式(9)，可得到

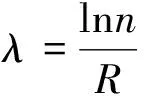
(10)

切口纵剖面面积为

则旋转射流旋转一周切割体积表达式为

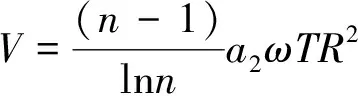
(12)

式中：ω为喷头切割旋转角速度，T为旋转一圈切割时间，R为喷嘴旋转一圈的极限切割岩石深度。

在磨料水射流切割过程中，喷嘴尺寸大小决定了射流切口宽度。可假定远端残余切口宽度与喷嘴直径相等，即

d=2a2

(13)

式中d为喷嘴直径。

将切口宽度与喷嘴直径关系代入式(12)，得

(14)

由于磨料射流对材料的体积去除量几乎完全由于磨料粒子侵蚀动能决定，射流对材料的体积去除量主要是磨料粒子的削切作用，故射流切割总体积可近似表示为单个磨料微粒对材料的体积去除量乘以磨料微粒的总数，即

(15)

式中：Qa为磨料流量，m为单个磨料微粒的质量，Vs为理想状态下单个磨料微粒对于材料的去除体积。

根据以上数学模型与实际磨料去除体积联立可得

(16)

由式(16)可得磨料旋转射流旋转一圈的射流切割深度为

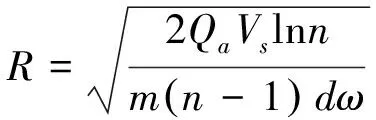
(17)

2.3 环形磨料水射流磨料速度估算

从式(17)可得，射流的切割深度主要与磨料流量、切口宽度与残余宽度比、单颗磨料去除岩石体积、喷嘴直径以及割缝器旋转角速度密切相关。根据射流经验参数估计，磨料流量、喷嘴直径及割缝器旋转角速度均为已知量，为求得环形射流切割岩石深度，需对磨料速度进行估计。假设水为不可压缩流体，根据伯努利方程，则高压水速为

(18)

式中：vw为磨料水的速度，p为射流喷射压力，ρw为水的密度。

在磨料水射流中，磨料微粒的运动速度完全依靠高压水提供，所以磨料微粒在与高压水混合后的运动速度与高压水速度几乎相同，根据动量定理

Qwvw=a(Qw+Qa)va

(19)

化简可得

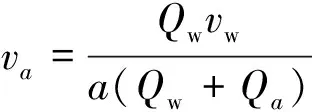
(20)

将式(18)代入式(20)，得磨料速度表达式为

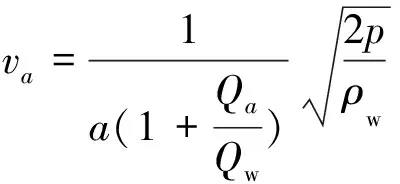
(21)

式中：a为动量传递系数，理想状态下取1；Qa为磨料流量；Qw为高压水的流量，va为磨料在喷嘴处速度。

根据磨料在外流场中的运动受力情况，可知磨料在外流场中的运动速度随射流距离的变化而变化，呈现先增大后减小的变化趋势，导致单颗磨料对于材料的去除体积量也在产生变化。因磨料粒子运动受力机理复杂，在此，进行磨料运动速度的理想化假设。假设磨料在外流场中处于理想运动状态，即磨料粒子速度为射流喷出的速度。在先增大后减小的磨料速度变化曲线中，喷嘴处的磨料速度可视为磨料先增大再减小速度的均值，因此理想化假设可类比实际磨料在外流场中的变化规律，即

(22)

式中vs为磨料在外流场中速度。

2.4 磨料水射流切割深度模型准确度验算

为验证环形磨料射流单颗磨料对于材料去除体积的准确性，结合现有数据，对特定工况下磨料水射流切割泥岩进行算例分析。依据式(17)，可得一定切割深度下，喷嘴旋转切割一圈的单颗磨料去除材料体积量表达式为

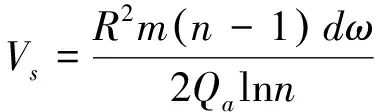
(23)

根据已有文献中磨料水射流切割泥岩的试验数据[24]，试验中射流切割时间为10 min，假设旋转切割单圈材料去除体积相同，则单圈射流切割深度可表示为总体切割深度除以10 min内射流旋转圈数，将已有工况参数以及计算数据记录于表3。

表3 算例验证工况

将算例基本工况参数代入式(23)，可知文献中切割一圈磨料水射流单颗磨料去除泥岩的体积为1.774 7E-16 m3。

理想磨料射流切割状态下，单颗磨料粒子对于泥岩的去除体积量可按式(5)计算，计算过程中所需参数值如表4所示。

表4 算例验证参数

则单颗磨料去除泥岩体积与单颗石英砂磨料冲击速度之间的关系如图4所示。

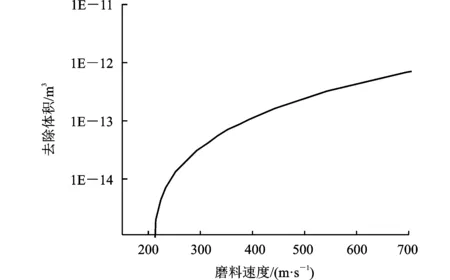
图4 单颗磨料去除泥岩体积与冲击速度的关系

根据图4，结合实际射流时磨料对泥岩的去除体积量为1.774 7E-16 m3，在图4中，寻找理想射流条件下达到此泥岩体积去除量的磨料速度，示意如图5所示，可得磨料射流中磨料微粒的运动速度需达到209 m/s，此时磨料对泥岩的体积去除量为1.773 6E-16 m3，与1.774 7E-16 m3大致相当。

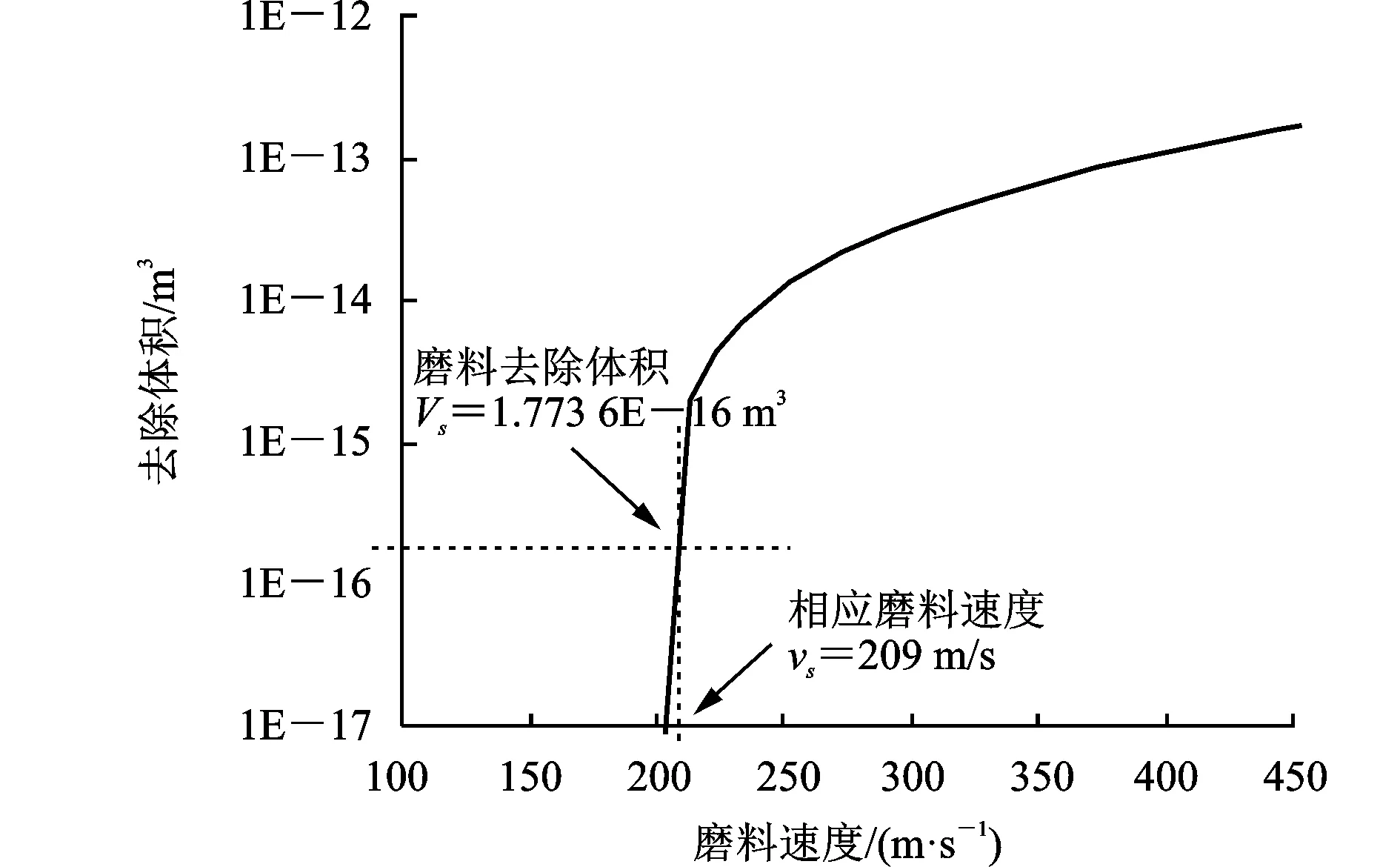
图5 泥岩算例磨料速度

假设磨料速度vs与水速vw相同，将磨料速度代入

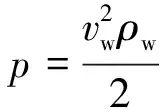
(24)

计算得到单颗磨料去除岩石体积理论模型计算下的射流压力为21.84 MPa，对比实际算例下射流压力25～30 MPa区间，差距较小。考虑到实际切割过程磨料粒子在外流场中的能量衰减，可见基于单颗磨料去除材料体积模型下的岩石切割深度模型准确度较好，可用于计算磨料水射流切割岩石工况。

3 磨料水射流切割岩石极限深度估算

3.1 射流中磨料的发散和衰减

根据磨料水射流切割截面分析可知，磨料射流切割岩石切口形状因射流的发散作用而呈现“V”字形减小的变化现象。在核心射流区域(即射流轴线方向)磨料流量保持原有流量大小，所有磨料粒子均对待切割材料造成去除破坏，而越接近射流边界，由于射流束发散现象的存在，射流边界附近磨料流量减小，其对射流边界处材料去除体积的减小，导致切口沿射流方向的“V”字形减小，分析可得磨料流量的大小变化是切口沿射流方向逐渐收敛的主要原因。

磨料射流中，磨料对材料的去除体积与作用在材料上的颗粒数有关，作用在切割面上的磨料越多，其对材料的切割效果越好，表现为去除材料总体积的增大。对于二维射流切口，材料整体体积减小系数可用对应线段长度之比表示。如图6所示，线段AB为起始射流切口宽度2a1；线段HI为极限切割深度下的切口残余宽度2a2，线段DE为喷嘴割缝器旋转一圈后的残余切割宽度。曲线AH、BI为实际射流切割岩石边界；曲线AG、BJ为理想射流发散边界。磨料射流切割过程中在射流切割线处的切割体积可由线段DE表示，因射流发散作用而未切割的材料体积可由线段CD与线段EF之和表示。故射流中损失的磨料颗粒量亦可按照(lCD+lEF)/lCF表示，则具有切割效率的磨料流量为lDE/lCF。

图6 磨料流量衰减计算示意图

已知，实际切口宽度2a1/2a2之比为n，假设射流发散边界走势与射流切割边界走势类似，则射流发散宽度2c2/2a1之比也为n。借助等分手段，将线段OL分成i份，则线段OK为第t圈旋转切割深度，记为t，线段KL则记为i-t，线段OL为总切割时长。定义磨料流量衰减系数α，根据相似关系，则有

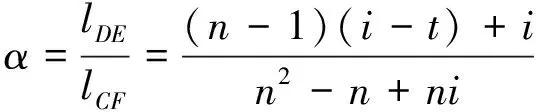
(25)

3.2 环形磨料水射流极限切割深度估算方法

根据式(17), 在考虑磨料流量损失的情况下，割缝器每旋转一圈的切割深度依次表示为

R0=R0

⋮

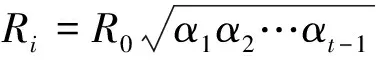
(26)

可得，若射流切割总时间确定，通过等分法可对射流总切割时长进行划分，并以单位时长旋转切割1圈作为等分段，计算该段内磨料射流切割深度，并对所有射流等分段内切割深度累加，得射流极限切割深度。则磨料射流极限切割深度可表示为各段切割深度之和，即

R=R0+R1+R2+R3+…+Rt-1

(27)

式中R为岩石切割深度。

割缝器旋转角速度(即旋转周期)不同时，总切割时长可划分为不同数量等分切割段，借助不同等分段不同切口宽度比值模拟磨料粒子因射流发散造成的衰减。根据定义的磨料流量衰减关系，理论上射流等分数量不同，磨料流量衰减率不同，射流在每等分段上的岩石去除体积不同，故切割深度不一。另外，射流等分段数量与磨料流量衰减系数呈负相关，射流等分的数量不会对整体射流极限切割深度估算造成巨大误差，整体吻合度较好。

3.3 围岩磨料射流切割施工算例分析

在施工中，裂隙厚度与长度可作为磨料射流切割洞库围岩的施工指标，其对洞库裂隙防护群的消波抗爆影响重大。根据现有洞库围岩的质量等级，对磨料水射流环形切割围岩的相关施工参数进行分析。

2个算例分析均采用石榴石磨料，分别以不同射流压力、不同喷嘴旋转角速度(周期T)、不同磨料流量对花岗岩及砂岩进行切割算例计算，工况见表5。

表5 极限切割深度算例工况

根据表5中算例工况参数，分别对岩石的切割能力进行估算，并将各段切割深度绘制成图，分别如图7和图8所示。

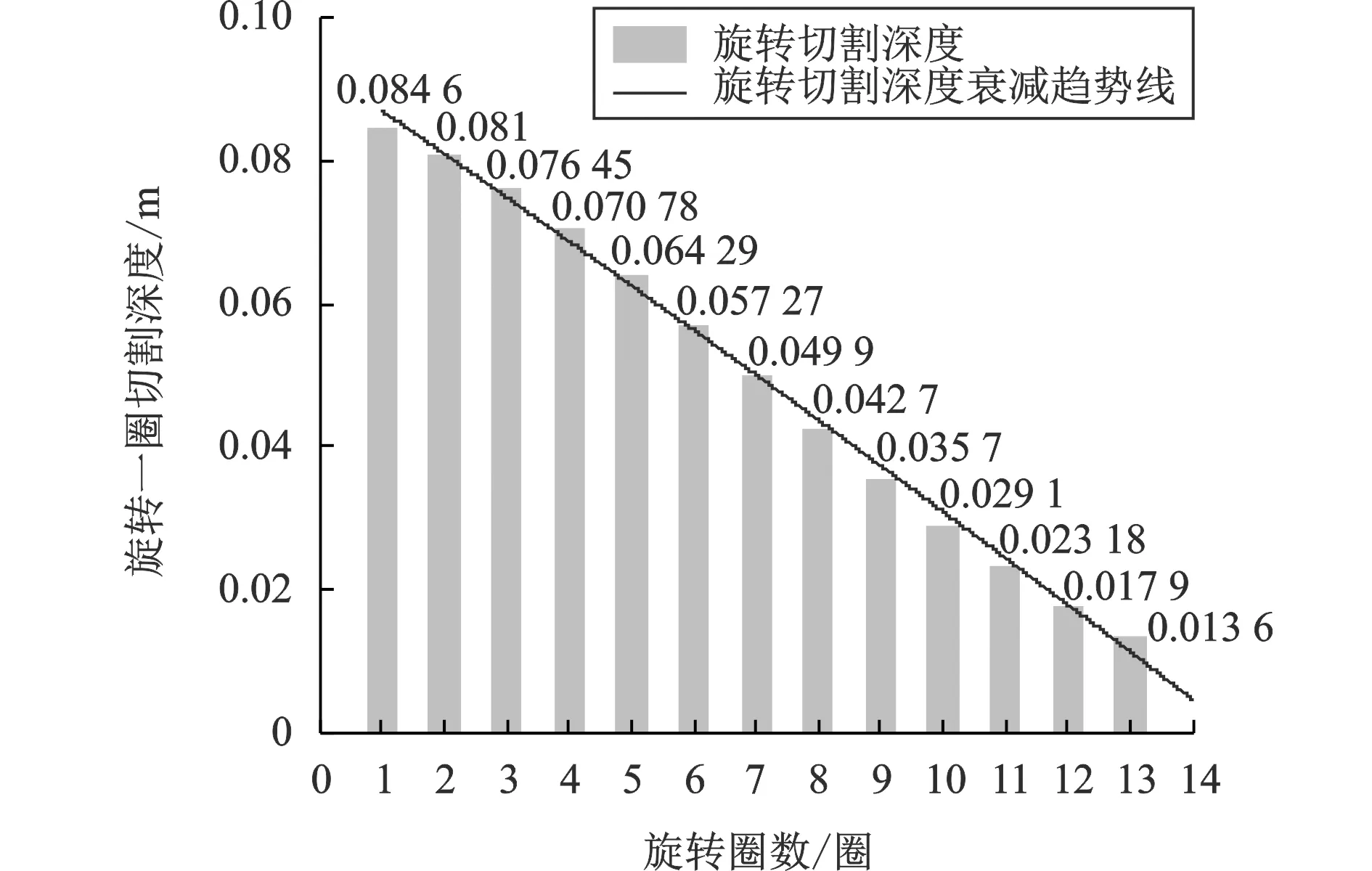
图7 磨料射流对花岗岩切割深度(算例1)

图8 磨料射流对砂岩切割深度(算例2)

在算例1工况下，根据图7，在施工10 min时，割缝器每旋转一圈，其对花岗岩的切割深度不同。第1圈切割深度为0.084 6 m，1～2 min内旋转切割深度约为0.081 m。随着切割深度的增大，单次旋转切割对于花岗岩的切割深度逐渐减小。根据图7趋势线预测，旋转第15圈时，即切割时间为15 min时，磨料水射流对于岩石的切割作用微乎其微，可暂停切割。对单圈切割深度计算总和，可得使用60 MPa喷射压力、3 mm喷嘴、0.3 mm石榴石磨料等参数下的切割花岗岩极限深度约为0.646 m。

算例2工况下，根据图8，可知在射流压力为30 MPa、增大磨料流量至0.2 kg/s时，在切割13～14 min时对于砂岩的极限切割深度约为1.16 m。对比算例1，相较于射流压力和射流速度，材料的硬度变化对于围岩磨料射流切割能力影响最大。随待切割材料的硬度等参数的增大，磨料水射流的切割效率下降，面对硬岩(花岗岩)的制缝深度约为切割砂岩的55.7%。

根据射流切口形状，射流切口主要沿射流轴线方向呈水楔形递减。初始射流切口宽度为5 mm左右，残余切口宽度约为3～4 mm，考虑到岩石材料脆性破裂现象，切口旁围岩也已经受到削切破坏作用，故实际单次切割切口宽度应大于5 mm。所以可上下调整割缝器位置，对围岩进行多次切割，可满足在围岩中构建宽度厘米级别、长度米级别的人工裂隙群。

4 结论

本文围绕磨料水射流技术对围岩的割缝性能，综合数学理论建模与理论推导构建了磨料射流切割岩石体积量模型，提出了磨料射流切割岩石极限深度计算方法，并验证了其在特定工况下的准确性，主要结论总结如下：

(1)构建了磨料水射流切割中磨料粒子运动速度与切割岩石体积量关系，得到了不同磨料速度下石榴石磨料粒子对于砂岩、花岗岩等岩石的体积去除量。

(2)基于射流的发散现象，分析了磨料射流理想化切口形态，并依据理想化射流切口，构建了环形磨料射流体积去除量方程，推导了环形石榴石磨料射流切割特定岩石材料深度模型。基于本文数据，可得该理论模型计算下的射流压力为21.84 MPa，考虑到实际切割过程中的能量衰减，与实际算例下射流压力25～30 MPa的差距较小，验证了该理论模型的准确度。

(3)根据磨料射流理想化切口形态，定义了磨料射流中磨料流量的衰减系数。通过将射流切割时间等分并结合环形磨料射流切割岩石深度模型，推导并提出了环形磨料射流切割岩石极限深度计算方法。对不同压力、不同流量等参数工况下磨料射流切割花岗岩、砂岩进行了算例分析，得到了特定工况下磨料射流切割以上岩石的理论极限深度。此外，对射流切割裂隙厚度也进行了相应探究，综合为施工时射流参数选择提供依据。

(4)根据模型估算结果，磨料水射流环形切割花岗岩0.646 m，砂岩极限深度1.16 m，其割缝性能满足洞库围岩人工致裂进而构建抗爆消波防护层的性能要求，在地下防护工程施工中具有合理运用前景。但是，后期不可忽略围岩人工磨料水射流切割致裂对于洞库及围岩的稳定性影响。