例谈探究式教学在中学数学中的应用

胡怡

摘要：探究式教学教育改革的一把利剑。为了更好的利用探究式教学，将探究式教学分为数学探究和数学微探究;再分别介绍数学探究和数学微探究的概念，适用范围，以及教学示例。培养学生发现问题，提出问题，分析问题，解决问题的能力;

关键词：探究式教学;数学探究;数学微探究;

中图分类号：G4 文献标识码：A

1.背景

在教学实践中，什么样的数学课堂需要用到“数学探究”？教师是否应该生搬硬套“数学探究”的全过程？“数学探究”是否真的应用广泛，是否提高了学生的自主学习能力和数学素养？事实上，我们在摸着石头过河，我们对于数学探究的应用还比较弱。

2.数学探究与数学微探究

2.1数学探究

2.1.1数学探究的概念

数学探究对学生的知识基础和老师的教学能力有着较高的要求，并且需要的课堂教学时间更长，完整的流程一般要20分钟甚至一节课的时间。它更加适合学生难以理解的抽象程度较高的数学定理公式，以及整个探究过程对学生的思维，能力，品格有重大影响的活动。下面以初中勾股定理为例介绍探究式教学过程。

2.1.2.数学探究教学示例

勾股定理探究式教学过程[3]

（1）：创设情境，导入新课

出示任务一：用两个边长相等的正方形纸片，如何剪拼一个大的正方形？

启发学生：

①要拼成的大正方形和两个小正方形相比有何特点？

边长都大于两个小正方形的边长，大正方形的面积等于两个小正方形面积之和。

②如何找到大正方形的边？

将两个小正方形进行裁剪，最特殊的就是沿对角线剪开;四条对角线正好组成大正方形的边长。

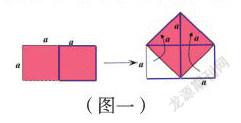
③剪拼过程如图所示（如图一）：用几何画板进行演示

（2）：层层递进，探索新知

出示任务2：把两个大小不同的正方形纸片剪拼成一个大正方形。

启发学生：

①任务一和任务二的条件和问题有何异同？

相同点：都是用两个正方形纸片拼成一个大正方形，总面积不变。

不同点：两个正方形从大小相同变成了大小不同。

②如果再沿两个正方形对角线剪开，两个正方形对角线边长一样长吗？

对角线一长一短。且对角线是在正方形中能剪出的最长线段。

③所以应该怎么剪？

將两个正方形并在一起。要使剪下的两条线段成为大正方形的边，要在两个连体正方形的下底边上找到恰当的分割点。然后将减下来的两部分移到上方，注意剪切的线段在外部。

剪拼过程如图二所示：

设置问题，发现定理

①对于任务二的这个过程，如何用面积的方式，将几何图形转化为代数描述？

答：设大正方形的边长为c，两个小正方形的边长分别为a，b则有c2=a2+b2

②任务二中边长分别为a，b，c的三条边有什么位置关系？数量关系呢？

答：组成了一个直角三角形，总结即为在直角三角形中，两直角边的平方和等于斜边的平方。用数学语言表述为：“在直角三角形中，若a，b为直角边，c为斜边，则有c2=a2+b2”。

3.2数学微探究

3.2.1.微探究的概念

由于数学探究耗费时间长，效率偏低，长期大量使用数学探究不仅不符合实际，而且难以在有限的时间内完成教学任务，达成教学目标。又基于探究理念在数学探究课堂中的重要性，这就走向了“中间地带”-数学微探究。

数学微探究不同于数学探究，它只是教学过程中的某一个环节，操作性强，能够较好的融入数学教学课堂，提高课堂效率。所谓微探究，就是在发现，提出，分析，解决问题等环节中，进行有指导的探究发现活动。这种探究既有数学探究的特色，又比数学探究灵活。

3.2.2.微探究的教学示例

以等差数列求和公式的学习为例，其教学目标之一是掌握等差数列求和公式，解决数列和的最值问题。此时增加一个微探究，对于学生掌握和应用求和公式都有很好的作用，同时还能让其体会其中的函数思想。

等差数列求和公式的函数特性微探究过程

探究：

（1）已知数列{an }前n项和为 Sn= n2+1/2 n . 请探究这个数列的通项公式，是等差数列吗？如果是，它的首项与公差分别是什么？当Sn最大时的序号n是多少？函数f（n）=n2+1/2 n ，n是实数，求使得函数值最大的n的值。

（2）如果这个数列的前 n 项和为 Sn=pn2+ qn +r ，其 中 p、q、r 为常数，且 p≠0，其结果是怎样的？

（3）已知等差数列2，8，14，20的前n项和为Sn ，求 使得 Sn 最大的序号 n 的值[5].

总结：求和公式的函数特性本身概念很好理解，不需要设计一堂探究课，只需要在上课过程中简单进行探究。但是又不能不探究，仅由老师告诉学生这个发现，学生缺少了自我推导发现的环节，在日后对于求和公式的运用就不会那么灵活。在数学课堂多多设置这样的微探究活动，时间不长，效率高，是在当下的课堂教学之下，提高课堂效率，提高学生数学素养的好方式。

4.总结与反思

数学探究式教学作为教育改革的一把利剑。在我们提出的二十年来缓慢发展，但是结合我国的教育现状也取得了不错的成绩。在教学中，要充分认识到各个因素的影响，采用不同的探究方式进行教学。

参考文献

[1]吴增生.郑燕红.勾股定理教学实验研究-让学生真正经历勾股定理的“再发现”过程[J].数学教育学报，2017，26（1）：2-4.

[2]苏红雨.基于问题设计的数学微探究评价体系构建[J].数学教育学报，2019，28（1）：5-6.

[3]普通高中数学课程标准教科书[M]北京：人民教育出版社，2004.