非齐次热方程侧边值问题的一种迭代方法
熊向团, 乔 宇
(西北师范大学 数学与统计学院, 甘肃 兰州 730070)
许多工业应用[1-2]中往往需要确定本身无法直接测量的物体表面的温度结构.此时,只能通过物体内部某个固定位置的温度测量值反演表面温度,这是一类经典的逆热传导问题,即热方程侧边值问题.一维齐次热方程侧边值问题表述如下:
(1)
该问题中,人们希望通过测量数据h(t),恢复0 (2) 运用最优滤波法得出正则解,并通过Fourier变换技术获得正则解的误差估计.Deng等[9]和Liu等[10]研究一个更一般的问题,即变系数抛物方程的侧边值问题: (3) 采用不同的迭代法求解,并证明该方法在先验和后验正则化参数选取规则下都是阶数最优的. 热方程侧边值问题是具有重要意义的严重不适定问题,但目前已有结果主要集中于齐次热方程侧边值问题的讨论.Triet等[11]和Nguyen等[12]使用先验正则化参数选取规则讨论更为复杂的侧边值问题.然而,先验取法依赖于解的光滑性条件,虽然便于理论分析,但难以验证.因此,实际计算中,需要使用基于数据误差水平信息和误差数据本身的后验取法.鉴于此,本文考虑以下非齐次热方程侧边值问题 (4) 式中:f(x,t)是热源,不恒为0.将问题(1)推广到非齐次情形(4),使用迭代正则化求解该问题, 并分别在先验和后验参数选取规则下得出稳定的误差估计. 为了在频域中考虑问题(4),将函数g(·),u(x,·)等出现在本文中关于t的函数延拓到整个实轴,并令其在t<0时为0.定义函数g(t)∈L2(R)的Fourier变换为 对问题(4)关于t作Fourier变换,得 (5) 等价地, (6) 式中 注1f(x,t)=0时,式(6)退化为 (7) 是问题(1)的解,即非齐次问题的解化为齐次问题的解,故本文的结果更一般. 实际测量中,只能得到噪音数据gδ(t),假设gδ(t)与g(t)满足: (8) (9) 此外,根据频域中解的表达式(5)可知,为了使得解有意义,需设 ∀ξ,C为正常数 (10) 引入以下迭代格式[6] 注2显然,迭代形式(11)与迭代形式(12)可整合为 (13) 应用迭代格式(13)求解问题(4),并给出先验参数选取规则下稳定的误差估计. 引理1[6]设0≤ω≤1,0≤α≤1,且n≥1,则以下不等式成立: 为方便计算,本文简记 由于 故记 证明记 以下分两步来证明. 由式(15)有 1-(1-ω)n≤(nω)1-x 再结合噪音假设式(8),得 即 (18) 由式(17)得 所以 结合先验界式(9),得 (19) 结合式(18、19)得 定理证毕. (20) 1)ρ(n)是连续函数; 4) 对∀n∈(0,∞),ρ(n)是严格递减的单调函数. 证明注意到x=1时,Q(ξ)=0.由Parseval恒等式及式(13)得 根据ρ(n)的表达式,1)和4)显然可得.由于 所以有 由此可得2)和3). 引理3假设不等式(20)成立,则n满足: (21) 证明由三角不等式,Parseval恒等式及式(20)得 所以 再结合不等式 由噪音假设(8)可得 即 证明记 则 由Parseval恒等式及Hölder不等式,得 即 其中 引理5以下不等式成立 证明由Parseval恒等式和三角不等式,得 因此,得 结合式(21),得 引理6以下不等式成立 证明由Parseval恒等式,三角不等式及噪音假设得 其中 证明由引理4~引理6,可得 其中 定理证毕. 本文使用迭代正则化方法克服一维热方程侧边值问题的不适定性,并给出正则解与精确解之间的Hölder型误差估计,证明了所用方法的有效性.同样,该方法可以用于解决多维问题,这有待于进一步研究.此外,当测量数据g(t)与非齐次项f(x,t)同时有扰动时可类似讨论. 致谢:本文得到西北师范大学科学计算创新团队项目(NWNU-LKQN-17-5)的资助,在此表示感谢.1 定义及说明
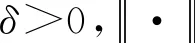
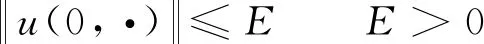
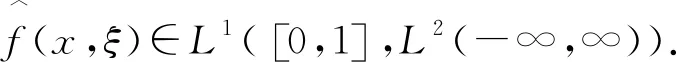
2 迭代正则化方法

2.1 先验参数选取规则下的误差估计
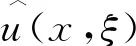
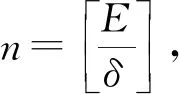
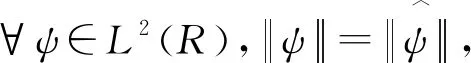
2.2 后验参数选取规则下的误差估计
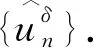
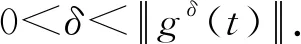
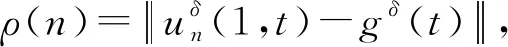
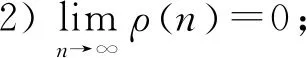

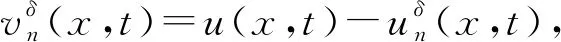
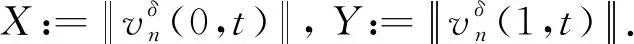
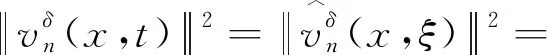
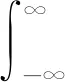

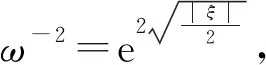
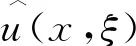
3 结论

