反舰导弹辐射源行为分析中的贝叶斯方法*

崔 凯，宋新超，秦长海

（1.江苏科技大学电子信息学院，江苏 镇江 212003；2.中国船舶重工集团第七二三研究所，江苏 扬州 225101）

0 引言

由于科技的提升使得现在的反舰导弹精确打击能力不断加强，这也要求海军舰队必须升级对抗反舰导弹的防御系统。世界各国经过一段时间的研究，已经有部分防御方式应用到实际，比如密集阵［1］、反导导弹［2］、诱饵箔条［3］、电子干扰等。

当反舰导弹发起进攻时，其辐射源通常会经历4 种行为［4］，如下：

1）搜索模式（Search Mode）。导弹发射出去一段时间后，导引头雷达开机，用于对目标进行搜索。

2）分类识别模式（Classify Mode）。当搜索到有目标时，会对目标进行识别并确认，此过程通常只有10 s 不到。

3）跟踪模式（Tracking Mode）。一旦制导系统确定了需要攻击的目标，便会进入该模式跟踪目标。

4）干扰寻的（HOJ，Home On Jamming）模式。如果导弹制导系统检测到目标正在释放电子干扰，其辐射源将会转为该模式并进一步提高反舰导弹在电子干扰下对目标的精确打击概率。

当舰队正在受反舰导弹威胁时，需要采取有效的防御措施。为了能够达到很好的防御效果，首先要对反舰导弹辐射源的行为以及行为变化进行判断分析，本文的研究重点就是以贝叶斯模型中常用的蒙特卡洛马尔可夫链算法（Markov Chain Monte Carlo，MCMC）对反舰导弹辐射源的行为以及行为变化进行有效分析预测。虽然反舰导弹辐射源有4 种行为模式，但在电子对抗研究领域，可以将搜索模式与分类识别模式归为搜索状态，将跟踪模式和干扰寻的模式归为跟踪状态，本文也重点研究反舰导弹辐射源的这两种行为状态。

1 战斗中反舰导弹攻防体系分析

以下是反舰导弹发起进攻以及舰队自我防御的示意图（图1）［5］。HVU（High Value Units）指海上高值目标，为反舰导弹重点攻击对象，战斗过程分为以下几步骤：

1）导弹发射出去一段时间后，其辐射源开机并开始搜索海面目标。

2）在距离目标10 n mile，制导系统已经成功定位目标并且导弹辐射源转为跟踪模式，反舰导弹开始追踪目标。

3）离目标还有8 n mile 左右时，HVU 上的设备开始释放出电子干扰来迷惑反舰导弹的制导系统。

4）距离舰队6 n mile 左右，此时的反舰导弹正受电子干扰影响，其辐射源可能已经转为干扰寻的（HOJ）模式并指引导弹继续追踪HVU，也可能会追踪电子干扰产生的虚拟目标。

5）如果导弹追踪虚拟目标或者诱饵箔条，HVU就会停止释放电子干扰。如果导弹仍然追踪HVU，则密集阵待命。

图1 反舰导弹进攻，舰队防御示意图

在对抗反舰导弹的防御过程中，最重要的一步就是释放电子干扰。释放干扰的时间不能过早，也不能过迟。如果过早释放干扰脉冲，会使反舰导弹辐射源提前转为干扰寻的（HOJ）模式，该模式下制导系统仍然会指引反舰导弹精确打击目标，航母编队照样受到威胁。如果太迟释放电子干扰，则为时已晚，舰队照样受到严重打击。

由于反舰导弹辐射源的行为从搜索状态转为跟踪状态时会有不到10 s 的时间对目标进行分类识别，所以要在其行为发生改变的那一瞬间释放电子干扰，才能对反舰导弹制导系统达到最佳干扰效果。因此，需要掌握的信息是，反舰导弹辐射源行为开始发生变化时，它与航母编队的距离是多少。

2 基于贝叶斯推理的基本概念

假设两个随机事件为D 和H，贝叶斯定理的公式［6］如式（1）所示：

如果将H 表示假设，D 表示数据，那么贝叶斯理论的定义就是在引入观测数据的前提下，假设成立的概率为多少。因此，在作贝叶斯分析时，以下几个参数特别重要：先验分布p（H）、似然分布p（D|H）和后验分布p（H|D）。p（D）为证据，也作边缘似然，但是对数据作贝叶斯分析时很少用到该项，大多数情况下也可以直接忽略。这样贝叶斯公式就有另一种表达方式：

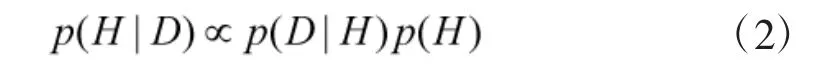
综上所述，在给数据作贝叶斯分析前，先要根据样本的状态选择合适的先验分布和似然分布［7］。现在的反舰导弹通常以主动雷达制导模式为主，本文就以反舰导弹辐射源的脉冲描述字（PDW）和导弹与HVU 之间的距离为原始样本，通过贝叶斯模型训练出PDW 不同的后验分布，根据不同的后验均值来判断出反舰导弹辐射源不同的行为状态以及行为发生变化的位置。

3 基于MCMC 的反舰导弹辐射源行为变化的估计

3.1 MCMC 基本原理

MCMC 是所有贝叶斯推理算法中常用模型［8］，其基本思路是：选择合适的抽样算法从条件概率分布中进行采样，结束后得到样本的后验概率分布，并将后验结果作为正态化常数。

此方法分为马尔可夫链和蒙特卡洛两部分［9］，马尔可夫链是表达数据状态转移的随机过程，而蒙特卡洛方法是对数据的抽样过程。MCMC 的原理［10］是将随机过程马尔可夫链引入蒙特卡洛抽样中进行模拟，在模拟过程中对样本进行抽样训练得到另一个马尔可夫链。本文就将雷达及侦察设备捕获到的反舰导弹辐射源的PDW 数据作为马尔可夫链状态样本，当经过多次模拟后，再基于这些样本进行随机抽样评估。

假设随机过程{Xn，n∈N}的初始状态为X0，自然数集N 表示随机过程的时间参数，I 为随机过程的状态参数集，令状态ai∈I 为随机过程所有可能状态。对于任意n∈N 以及a1，a2，a3，…，an+1∈I，条件概率满足以下公式：

则称{Xn，n∈N}为马尔可夫链，且当n→∞时，Xn与初始X0状态无关。在马尔可夫链中，随机变量的分布收敛于稳态分布π（x），称为马尔可夫链的收敛，那么在反舰导弹辐射源的PDW 值在后验分布中，其概率密度函数f（x）关于π（x）的期望为：

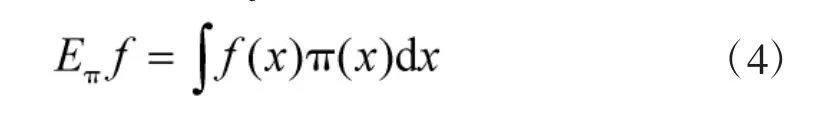
3.2 反舰导弹辐射源行为变化估计的全过程

根据上述MCMC 的原理，通过MCMC 对反舰导弹辐射源行为及行为变化进行估计的步骤如下：

1）以反舰导弹辐射源的PDW 数据为训练样本X，以反舰导弹与HVU 的距离为行为发生变化参数，参数集I 为搜索状态和跟踪状态两种行为。

2）选取某一处的PDW 值记为X0，从X0开始，利用马尔可夫链方法对飞行中的反舰导弹PDW 值产生点序列X1，X2，…，Xn。

3）马尔可夫链经过多次迭代后，各处PDW 的边际分布都是平稳分布，因此，最终马尔可夫链收敛。收敛后的后验结果就是反舰导弹辐射源PDW的期望值。

4）根据PDW 在不同行为状态下的两种不同的期望值，得出反舰导弹辐射源行为发生变化的位置。

3.3 Metropolis-Hastings 算法

蒙特卡洛方法是各类抽样算法组成的，其中Metropolis-Hastings 算法是一种比较常见的抽样法，Metropolis-Hastings 算法的步骤如下［11-12］：

4 实验仿真与分析

4.1 实验环境介绍

本文的实验环境是基于python3.6 语言，用于贝叶斯分析的python 库PyMC3 3.0 和用于可视化的Python 库Matplotlib 2.0.2。

4.2 实验过程分析

假设反舰导弹正在对HVU 发起进攻，同时舰队上的雷达以及侦察设备检测到导弹辐射源的PDW 值和位置（导弹与HVU 的距离）并记录在数据库，仿真实验以载频（RF）、脉冲幅度（PA）和脉冲重复周期（PRI）3 类PDW 参数为原始样本。它们的关系分别如图2～图4 所示。

图2 反舰导弹在不同位置的载频

图3 反舰导弹在不同位置的幅度

图4 反舰导弹在不同位置的PRI

如果仅仅观察3 张关系图，或许不太容易直接观察出反舰导弹在何处其辐射源行为发生变化，接下来就借助MCMC 方法进行分析，首先对载频（RF）进行数据分析。

对于距离disRF，很难选择它的先验。在贝叶斯分析中，如果先验分布比较难选择，通常就用一定范围内的均匀分布表示先验。因此，dis 的先验为均匀分布：

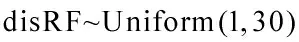
似然的选择：从图中可以看出数据是离散形式，而泊松分布能模拟计数类型的数据，设Di表示反舰导弹在i 处的载频信号大小。因此，似然的选择为：

选好合适的先验和似然后就可以进行仿真了，本次实验用Metropolis-Hastings 算法对数据进行采样，采样次数设为20 000 次。载频分析完后，再继续对PA 和PRI 进行分析，方法和步骤与上述相同。用PA 和PRI 作原始样本时，分别假设反舰导弹与HVU 的距离为disPA 和disPRI。

4.3 实验结果分析

由于要掌握反舰导弹辐射源行为发生变化时的具体位置，因此，只要观察disRF，disPA 以及disPRI 的后验结果。结果如图5～图7 所示。

图5 disRF 的后验分布

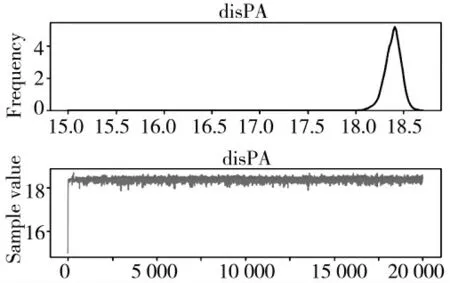
图6 disPA 的后验分布

在上述的3 组后验分布里，每组上图为核密度估计，是平滑后的频率直方图，最高点表示频率最大。下图是马尔可夫采样链，如果发现它在某一值附近振荡，说明收敛状态较好。初步观察，disRF 和disPRI 的后验分布没有收敛。后验分布收敛较好的是disPA，仔细观察其后验分布，它的核密度估计在18.5 左边频率最大，它的马尔可夫采样链在18 的上方某处振荡，因此，可以初步判断反舰导弹离HVU 为18 km～18.5 km 之间时，其辐射源行为发生变化。

图7 disPRI 的后验分布

disRF 和disPRI 无法收敛的原因是导弹辐射源行为发生变化时，RF 和PRI 的均值始终保持不变。当继续观察最初的PDW 数据时，可以发现RF 的变化范围不大，但是PRI 的抖动范围是有变化的，所以是否可以通过PRI 抖动的范围不同来判断导弹辐射源行为发生变化的位置，接下来就继续通过实验仿真来验证，步骤如下：

1）首先计算出所有不同位置的PRI 与导弹飞行过程中所有PRI 均值的差的绝对值，结果如图8所示：

图8 各处PRI 与PRI 均值的差的绝对值

2）以所有PRI 值与它们均值差的绝对值为训练样本，步骤与4.2 节所述相同，这时假设反舰导弹与HVU 的距离为disPRI2，它的后验如图9所示：

disPRI2 的后验结果中，核密度估计在18.5 右边频率最大，而马尔可夫采样链中，也在18～19 之间的某处振荡，因此，可以判断反舰导弹离HVU 的距离18.5 km 左右，其辐射源行为发生变化。

除了观察后验分布的核密度估计和马尔可夫采样链外，在PyMC3 中还能使用summary 函数得到具体的后验分布均值（mean）、标准差（sd）和蒙特卡洛误差（mc_error），这些值也可以用来分析后验结果。结果如表1 所示：

表1 disRF，disPA 和disPRI 的后验结果

在MCMC 中，希望sd 和mc_error 越小越好。如果mc_error 小于sd 的5 %，则可以说明收敛精度高。表中disRF 和disPRI 的这两个值都偏大，disPA和disPRI2 的这两个值比较小，且也满足收敛精度要求。根据表中disPA 和disPRI2 的后验mean 结果，仍然可以判断出当反舰导弹距离航母编队18.5 km 左右时，其辐射源行为发生改变。

4.4 实验误差分析及总结

上述仿真中，用于训练的PDW 的每类参数样本都很多。如果训练样本变少，后验结果又如何？图8 中，现在每0.4 km 取一次值，使得原始样本只剩下70 个左右，设disPRI3 表示此时的反舰导弹与HVU的距离。样本原始分布图和仿真后的后验分布分别如图10 和图11 所示：

图10 减少样本后的各处PRI 与PRI 均值的差的绝对值

图11 disPRI3 的后验分布

disPRI3 的后验分布中，核密度估计有3 个峰值，马尔可夫采样链的振荡范围也偏大，很显然与disPRI2 的后验相比disPRI3 的后验分布要模糊得多。

通过上述的实验结果，可以得出以下结论：

1）由于仿真实验中的反舰导弹辐射源的行为发生变化时，载频的变化范围不大，因此，很难通过单一频域来判断其辐射源的行为变化。

2）其辐射源的行为发生变化时，幅度的变化是很明显的，而且幅度的均值也会变化，因此，通过幅度就可以分析出结果。

3）仿真实验中的反舰导弹辐射源行为发生变化时，PRI 的均值始终不变，因此，仅仅通过PRI 也无法推断反舰导弹辐射源行为变化，但是根据PRI的抖动范围不同继续分析就得到预想的后验结果。因此，必要时要对原始样本进行适当的预处理来简化计算过程。

4）通常反舰导弹辐射源行为发生变化时，辐射源的时域、频域或能量域会发生变化，因此，在分析其辐射源行为及行为变化时，要从辐射源的时域、频域和能量域等多种角度综合分析。

5 结论

本文以MCMC 方法，通过对反舰导弹辐射源的PDW 中的3 类参数进行研究处理，并判断其行为以及行为在何处开始变化并完成仿真，仿真过程和结果表明，用该方法判断反舰导弹辐射源的行为以及行为变化理论上是可行的，也充分证明贝叶斯模型在推理应用中的高效性。

但是贝叶斯模型的缺点也很明显，可以归纳为以下两点：1）用贝叶斯作推理时，要根据训练样本的状态选择合适的先验分布，有时先验分布不是特别容易判断，如果先验分布选择不当就会导致后验结果无法收敛；2）另外用于模型训练的原始样本也要足够多，如果原始样本太少，后验的收敛效果也不会太好。