离心泵叶轮叶片轴向切割设计方法研究
赵万勇, 梁允昇, 彭虎廷, 马得东
(兰州理工大学 能源与动力工程学院, 甘肃 兰州 730050)
当今泵站中离心泵实际流量高于输水系统所需的问题普遍存在,离心泵工作在偏工况,不仅会造成电能的冗余和浪费,也会严重影响离心泵的运行可靠性[1].出于节能并降低泵站维护运行成本的目的,通过修改离心泵叶轮结构的方法减小离心泵的工作流量,使其工作在高效率区域.由理论分析可知,叶轮外径影响离心泵的扬程,且切割叶轮外径的方法由于简便易行成本低廉,被广泛采用,国内外学者对此展开过诸多研究.袁寿其、高振军、汪岩飞等[2-5]分别就叶片数、叶片进口角、叶片出口角与叶片包角等参数对离心泵性能影响展开过研究.对于切割叶轮外径的相关研究更为详尽.宇晓明等[6]归纳了叶轮外径斜切不同方向、不同角度下离心泵性能的变化,发现斜切能抑制小流量工况下叶轮出口的回流现象,有效消除了H-Q曲线上的驼峰.冷洪飞、荆野等[7-8]通过数值模拟方法,对离心泵叶轮外径切割公式的适用范围以及精度进行修正.Jain等[9]建立了相关经验公式预测切割叶轮直径与效率变化之间的关系.QU等[10]提出了一种新型抛物线切割方法,并对比了直切、斜切、三角切等几种对泵性能的影响,发现抛物线切法能有效改善叶轮出口压力分布并降低轴功.Barrio等[11]发现作用在叶轮上的压力脉动与径向力的振幅均随着外径切割而减小,但波动周期有所提高.司乔瑞等[12]通过噪声实验发现临界空化余量随着叶轮外径切割量增加而减小.
除此之外,轴向切割叶片平移叶轮前盖板以减小叶轮内出口流通面积从而改变离心泵性能的方法同样具有理论依据.由于技术与成本的原因相关研究鲜少进行,但随着计算机技术的发展,数值模拟方法使原来难以展开的课题得以实现.另外,对于提灌泵站的大流量双吸离心泵,其叶片由钢板冲压成形后与加工好的前盖板焊接成一体,若在焊接之前按照前盖板的形状轴向切割叶片,那么焊接后其叶轮前盖板相对原型轴向平移了一段距离,不改变原叶片形状与模具,不增加制造成本,方便可行,具有一定的工程价值.
1 计算模型与网格的划分
1.1 离心泵模型
本文的研究模型为单级双吸离心泵.模型泵M1的主要性能参数包括:设计流量Qd=790 m3/h;设计扬程H=34.12 m;比转数ns=176.4;转速n=1 450 r/min;叶轮进口直径D1=208.4 mm;叶轮出口直径D2=355 mm;出口宽度b2=35.85 mm;叶片数z=6.为了便于计算,忽略密封环间隙等部位,计算模型主要包括叶轮、半螺旋吸入室、螺旋压水室以及进出口延长段,如图1所示.

图1 模型泵M1网格划分
同时选用另一台比转数相近、但叶轮尺寸不同的单级单吸离心泵作为验证模型M2,该模型将用于检验本文所推导换算公式的有效性和通用性.模型M2的主要性能参数包括:设计流量Qd=50 m3/h;设计扬程H=20.54 m;比转数ns=129;转速n=2 900 r/min;叶轮进口直径D1=76 mm;叶轮出口直径D2=137 mm;出口宽度b2=14 mm;叶片数z=6,如图2所示.

图2 模型泵M2网格划分
1.2 研究方案
本文为了研究叶轮前盖板轴向移动对离心泵性能的影响,引入叶轮前盖板平移率Δb2,即前盖板轴向平移距离与原叶轮出口宽度b2的比值,如图3所示.不同叶轮前盖板平移率Δb2分别为5%、10%、15%、20%、25%、30%、35%、40%,同时,对比平移前盖板与切割叶轮外径对离心泵性能影响的差异,不同叶轮外径切割率ΔD2分别为5%、10%、15%.
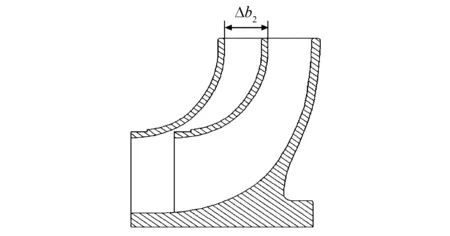
图3 平移叶轮前盖板示意图
(1)
式中:b′2为轴向平移前盖板后叶轮出口宽度;b2为原叶轮出口宽度;
(2)
式中:D′2为切割后叶轮外径;D2为原叶轮外径.
1.3 数值模拟方法
控制方程为雷诺时均N-S方程,采用RNGk-ε湍流模型,使用有限体积法进行离散,近壁面使用标准壁面函数修正湍流模型,动静耦合面采用多参考系模型,采用SIMPLEC算法耦合压力与速度,控制方程使用二阶迎风格式离散.
1.4 计算网格与无关性分析
本文基于ICEM前处理软件,考虑到计算的准确性和收敛精度,计算域在划分网格的时候采用六面体网格.对叶轮出口处和蜗壳隔舌网格进行局部加密;考虑到标准壁面函数的准确性,对全流道近壁面网格加密.为了减小计算误差,对同一工况下数值模拟进行网格无关性检验,结果如表1所列.当网格数增加到400万以后,数值计算所得的扬程相差最大小于2%.综合考虑准确性与计算效率,最终决定所有方案模型网格总数维持在450万左右,检验边界层最大y+值为104.
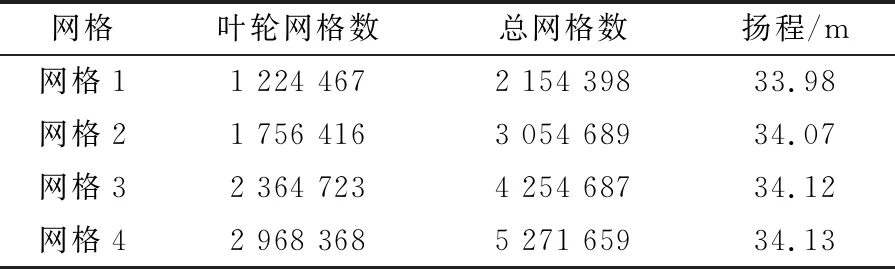
表1 网格无关性检验
2 数值计算方法
2.1平移叶轮前盖板对离心泵性能的影响
通过定常数值计算可以求得离心泵进出口的总压差值、叶轮壁面相对于转轴的扭矩以及扬程与效率.图4为模型泵外特性模拟值与实验值的对比.可以看出,当忽略了机械损失与泄漏损失后,模拟所得的数值略大于实验值,但最大误差在5%以内,且模型外特性的模拟值与实验值变化趋势基本相同,可以认为数值模拟具有一定的可信度.
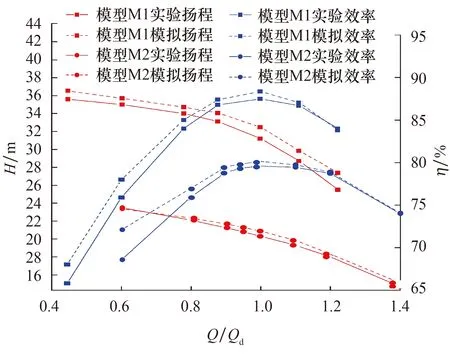
图4 模型泵M1与M2的数值模拟可靠性验证
图5分别为模型泵M1的H-Q曲线与η-Q曲线随着叶轮前盖板移动的变化图.由图5a可知,各工况下扬程均随着前后盖板间距减小而减小,当叶轮前盖板平移率达到40%时,0.78Qd工况点的扬程降低了4.87 m,而1.22Qd工况点的扬程降低了10.42 m,离心泵的H-Q曲线向下移动的同时变得陡峭.由图5b可知,小流量工况下离心泵效率随着叶轮前盖板移动而升高,0.78Qd工况点的效率最大上升量为1.9%;相反,大流量工况下效率随着前盖板移动而降低,流量越大下降幅度越大,1.25Qd工况点的效率最大下降量为9.515%,高效点略微下降且往小流量工况偏移.
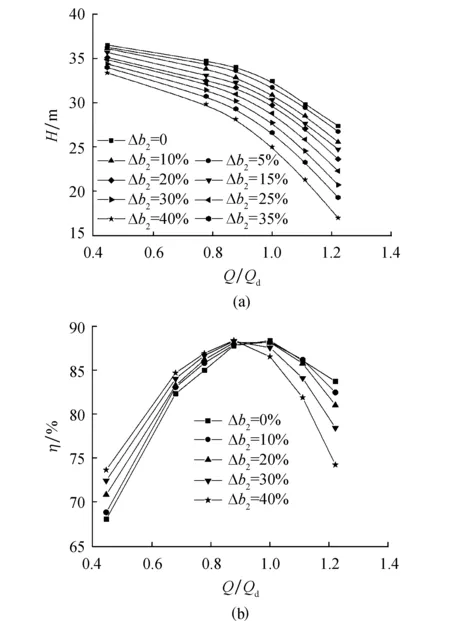
图5 不同叶轮前后盖板间距模型泵M1外特性曲线
2.2 叶轮前盖板平移与切割叶轮外径对离心泵性能影响的对比
图6为不同叶轮外径下模型泵M1的外特性曲线图.由图可知,H-Q曲线随着叶轮外径的减小而向下移动,当叶轮外径切割率为15%时,0.78Qd工况点的扬程下降了11.63 m,1.22Qd工况点的扬程下降了14.65 m.与平移叶轮前盖板相比,切割叶轮外径会使得离心泵小流量工况的扬程下降更为严重.
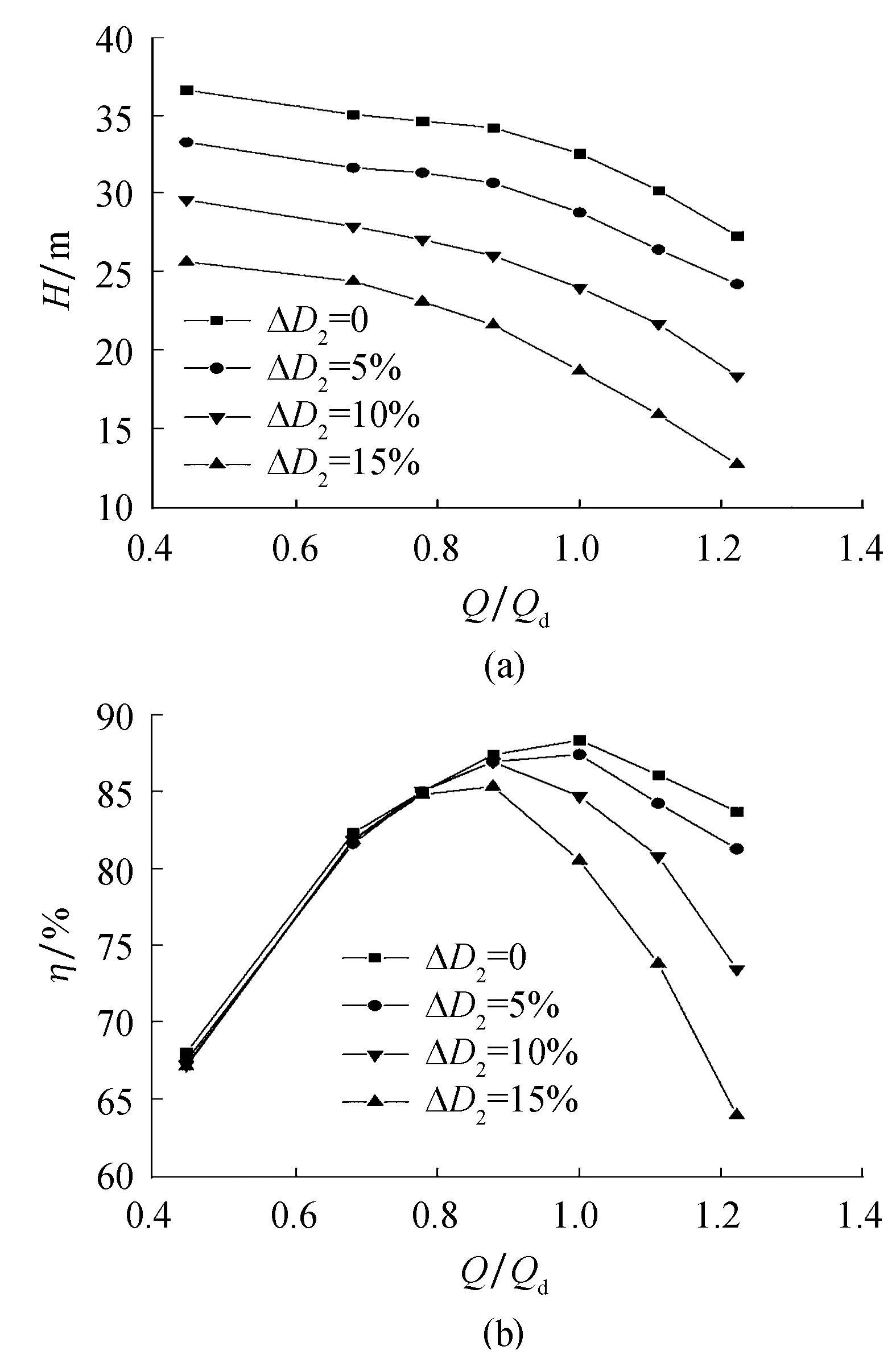
图6 不同叶轮外径模型泵M1外特性曲线
离心泵效率随着叶轮外径减小而下降的幅度与流量工况有关,如图6b所示.当流量低于0.78Qd时,模型效率基本上不随叶轮外径减小而变化.切割叶轮外径后叶轮出口与蜗壳进口之间的无叶片区域流动紊乱,湍流损失随着流量的增加急剧上升.当叶轮外径切割率为15%时,Qd工况点的效率下降了7.84%,而1.22Qd工况点的效率下降了19.79%.
图7为随着叶轮外径切割量ΔD2与前盖板平移率Δb2的增加,不同工况点下模型泵M1外特性变化的对比.由图7a可知,无论处于设计流量还是小流量工况,两种叶轮修改方案下离心泵的扬程均呈现下降的趋势.其中,切割叶轮外径所导致的扬程下降幅度更大,而平移叶轮前盖板后的扬程下降则较为缓慢.这是因为切割叶轮外径会直接减小叶轮出口圆周速度,理论上会降低离心泵的关死点扬程,使流量扬程曲线向下移动,而移动前盖板减小叶轮出口宽度理论上只会改变流量扬程曲线的斜率.所以与切割叶轮外径相比,轴向平移叶轮前盖板能使离心泵在减小流量的同时保持较高的扬程.
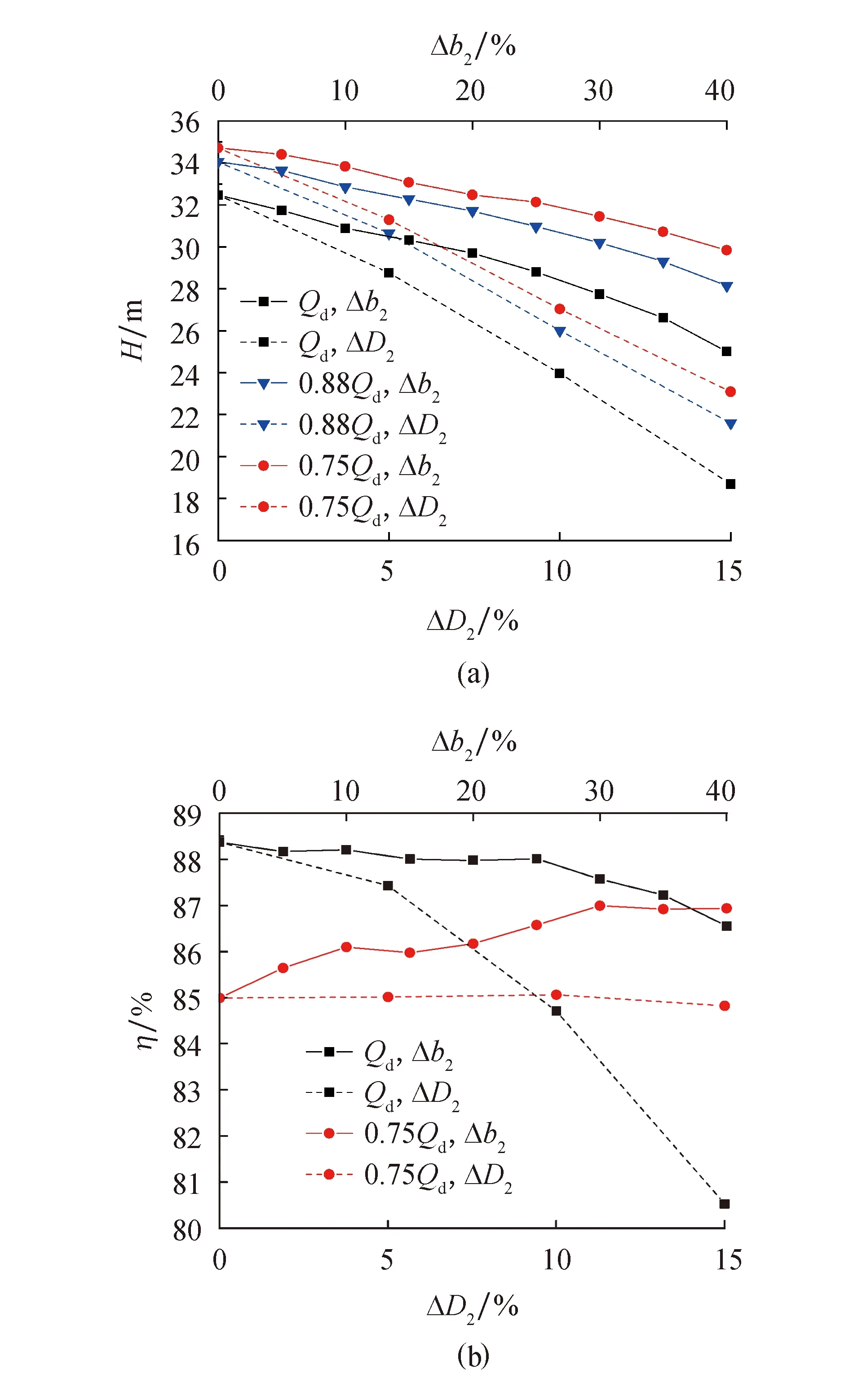
图7 不同工况点模型泵M1外特性随着Δb2和ΔD2的变化规律曲线
由以上分析可知,切割叶轮外径与平移叶轮前盖板均会使离心泵最高效率点向小流量移动,但不同的是,前者最高效率明显降低,而后者最高效率基本保持不变,高效区范围也没有明显变窄.图7b为离心泵效率随着ΔD2与Δb2增大而变化的对比图.设计流量下离心泵效率随前盖板平移的最大下降仅有1.67%,相比切割叶轮外径后最大下降了7.95%来说下降更为缓慢,而在小流量区域,离心泵的效率会随着叶轮前后盖板间距减小有所上升.这是因为平移叶轮前盖板能有效抑制小流量工况时叶轮内回流旋涡的发展,减小叶轮内的水力损失.而切割外径对叶轮内流动没有积极影响,相反,叶轮出口与蜗壳进口之间无叶片区域流动趋于紊乱,增加水力损失导致效率下降,如图8所示.
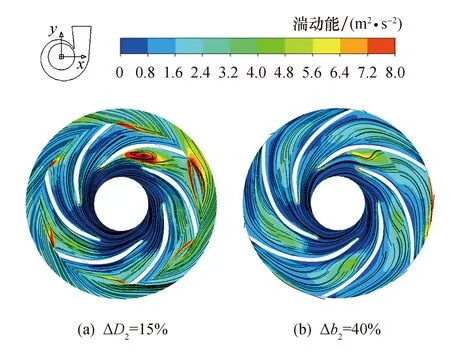
图8 0.65Qd工况下使用两种叶轮修改方法时叶轮内相对速度流线与湍动能云图
因此,相比切割叶轮外径,平移叶轮前盖板后离心泵流量减小的同时维持着相对较高的扬程和更高的效率.在大型泵站里减小叶轮出口宽度的泵比切割了叶轮外径的泵更适合于多泵并联工作.
2.3 预测轴向移动叶轮前盖板改变离心泵H-Q曲线
传统工程上使用切割叶轮外径的方法改变泵的水力性能,用切割定律定量地预测切割量与性能的变化关系,使用户切割叶轮外径后能准确得到需要的性能.因此,希望可以找到一种方法预测叶轮前盖板的平移率与离心泵性能变化之间的关系,使得这种方法更具工程价值.首先从泵的基本方程出发,研究前盖板移动对离心泵无限叶片数理论扬程HT∞的影响.由于叶轮前盖板轴向平移后叶轮入口宽度不变,为了简化问题,本文忽略前盖板平移后叶轮流道入口速度对离心泵理论扬程的影响.根据叶轮出口速度三角形化简公式,以及叶轮出口绝对速度的轴面分量vm2可以表示为泵实际流量与叶轮出口过水断面面积的比值,推导出离心泵无限叶片数理论扬程与泵基本参数之间的关系[13]:
(3)
式中:Q为叶轮出口流量,m3/s;u2为叶轮出口圆周速度,m/s;ω为叶轮旋转角速度,rad/s;k2为叶轮出口排挤系数;β2为叶片出口安放角,(°);vm2为叶轮出口绝对速度的轴面分量,m/s;ηv为泵的容积效率;b2为泵叶轮出口宽度,m;g为重力加速度,m/s2.
轴向平移叶轮前盖板后,叶片出口安放角、叶轮外径以及叶轮出口排挤系数均保持不变,容积效率也近似不变.当叶轮转速确定后,离心泵的无限叶片数理论扬程HT∞只与流量Q和叶轮出口宽度b2的比值有关.式(3)中,若将所有不随前盖板平移而改变的量都看作常数,将1/b2看作系数,Q为自变量,则HT∞=f(Q)为一次函数,斜率随着b2的减小而增加,这就是离心泵H-Q曲线随着前盖板的移动而变得陡峭的主要原因.
根据斯托道拉(Stodola)所推导的离心泵无限叶片数理论扬程和有限叶片数理论扬程差值的公式[13]分析,有限叶片数叶轮内相对速度偏移对理论扬程的影响与叶片数、叶片出口安放角、叶轮外径以及转速有关,与流量和叶轮出口宽度无关.因此,可以认为轴向平移叶轮前盖板对无限叶片数与有限叶片数的理论扬程具有相同的影响.同时由图7可以看出,设计流量下效率随着叶轮前盖板平移而下降的幅度很小,当Δb2增加到25%后效率才明显下降.可以假设前盖板平移量在较小的范围内时,设计工况点的效率近似不变且仍然是最优工况点,叶轮出口速度三角形也保持不变,蜗壳内流动基本保持最优状态,故叶轮出口绝对速度的轴面分量vm2不变.由于叶轮外径、叶轮出口排挤系数都是常数,所以在这个范围内平移前盖板后流量Q与叶轮出口宽度b2的比值也保持不变.根据式(3)可知,离心泵理论扬程不变.由此可以推导出离心泵扬程随着叶轮前盖板平移而变化的规律为
(4)
式中:Q′为前盖板平移后泵的流量,m3/s;H′为前盖板平移后泵的扬程,m.
式(4)是根据叶轮出口绝对速度轴面分量vm2保持不变和蜗壳内流动最优的假设推导出来的.由图7可知,前盖板平移量较小时,设计工况点效率没有明显降低,实际扬程与理论扬程一样保持不变,符合式(4)的使用条件.
图9为不同流量下式(4)换算的模型泵M1的H-Q曲线与数值模拟H-Q曲线的对比图.图中,在20%的前盖板平移量内,设计工况点通过式(4)换算的新工况点基本上都与数值模拟值相重合,可以认为通过理论推导的式(4)能在一定程度上预测平移前盖板后离心泵的扬程.但同时发现当流量偏离设计工况点后,换算出来的工况点与数值模拟值出现了偏差,偏差值随着流量远离设计工况点而增大.这主要是因为离心泵效率随着前盖板的移动而变化,水力损失使得实际扬程降低;同时根据式(3),理论扬程也会随着叶轮前盖板的移动而变化,特别是大流量工况下,叶轮出口宽度减小后,相同流量下vm2变化更明显.
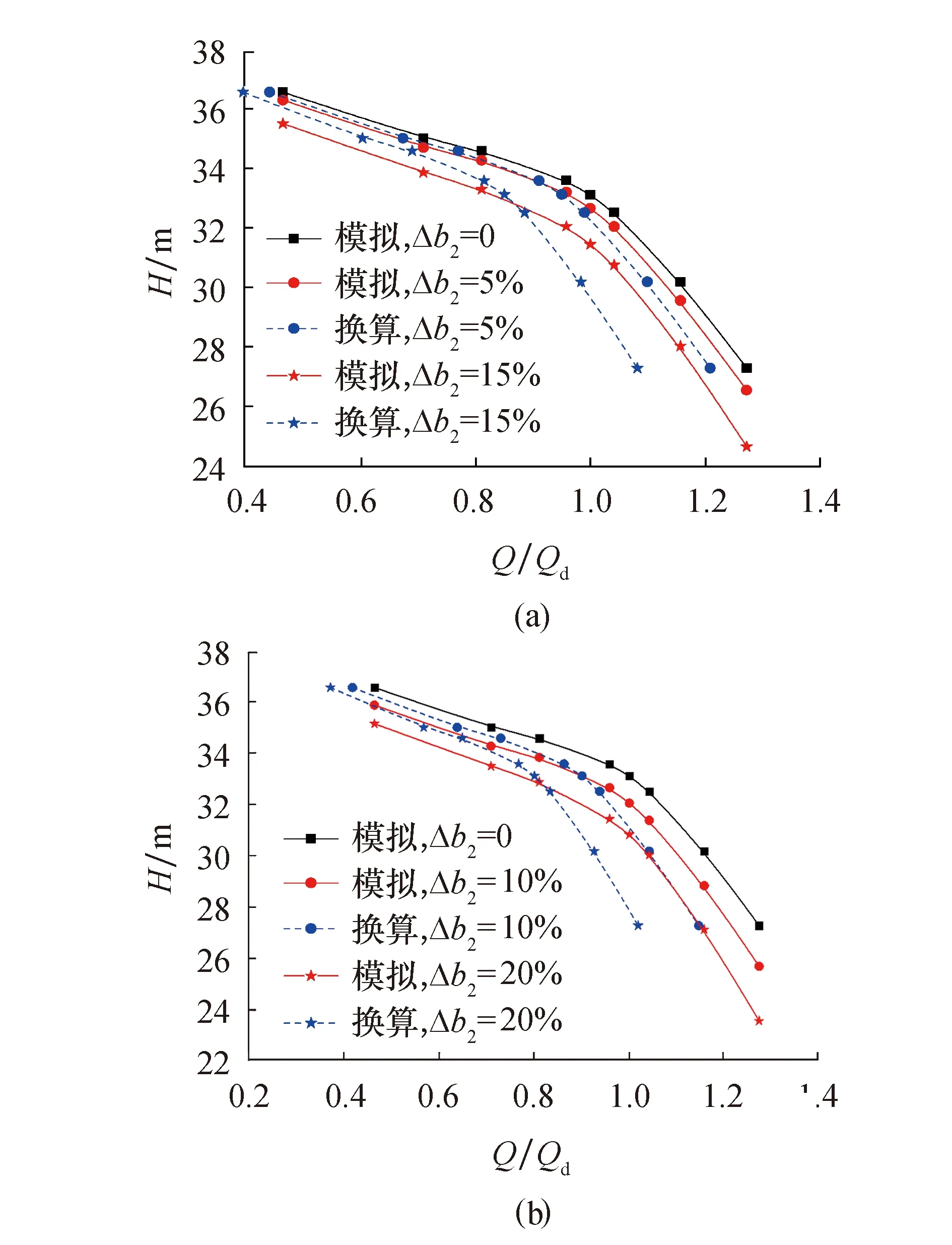
图9 模型泵M1数值模拟与公式换算的扬程对比曲线
因此需要对式(4)的扬程进行修正.考虑到扬程误差主要与水力损失有关,而离心泵内冲击损失和摩擦损失都和流量的平方成正比.因此把修正公式拟定为二次多项式,自变量为工况点流量和叶轮前盖板平移率Δb2,因变量为换算点模拟扬程与换算扬程的比值.根据自变量与因变量的关系修正公式为
(5)
式中:A、B、C均多项式系数;H″为修正后的扬程值,m.
以大量数值模拟数据为基础进行多元回归分析,拟合修正公式.由regress函数返还的回归系数及其检验统计量如表2所列.
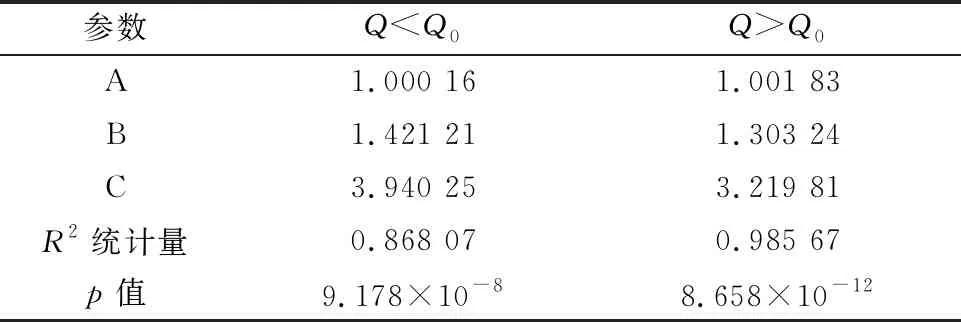
表2 regress函数的返还结果
检验回归模型统计量中,R2统计量分别为0.868、0.986,且F统计量的p值均相当小,因此可以认为拟合优度较高,拟合模型有效.把多元回归分析所返还的系数代入修正公式,并结合式(4),可以获得修正后的离心泵扬程与叶轮前盖板移动距离的换算公式:
(6)
Q Q>Q0K=1+1.3Δb2·ΔQ+3.22Δb2·ΔQ2 为了检验换算公式的有效性和通用性,以模型泵M2作为验证模型,将其实验数据通过式(6)换算成H-Q曲线,并与数值模拟曲线进行对比,如图10所示.当叶轮前盖板移动量较小时,公式换算曲线与数值模拟曲线有较高的拟合度;随着前盖板平移率增大,换算曲线的误差增大.无论叶轮移动距离大小如何,靠近设计工况及偏向小流量工况区域换算曲线拟合度较高,而远离设计工况点后换算曲线与模拟曲线偏离幅度增大,特别是大流量区域误差严重.因此,式(6)的理想使用范围是预测中比转数离心泵在较小前盖板平移量时、0.8~1.0倍设计流量范围内工况点的扬程变化,符合本文的研究目的,具有一定的工程价值. 图10 模型泵M2数值模拟与修正后公式换算的扬程对比曲线 1) 随着叶轮前盖板平移,各工况下离心泵扬程均下降,流量越大扬程下降幅度越大,离心泵H-Q曲线下降的同时变得陡峭.叶轮前盖板轴向平移,离心泵高效点向小流量工况偏移,小流量工况效率升高,大流量工况效率降低,η-Q曲线整体向左移动. 2) 与切割叶轮外径相比,平移叶轮前盖板后离心泵扬程的下降幅度更小,效率更高.特别是当离心泵工作在小流量工况时,平移叶轮前盖板后能有效抑制叶轮内的回流旋涡,离心泵的水力效率有所上升,扬程下降幅度更小,更适合于多泵并联工作. 3) 根据离心泵在最优工况流量下叶轮前盖板移动距离较小时叶轮出口绝对速度轴面分量不变的假设,理论推导出离心泵扬程随前盖板平移而变化的预测公式,并根据数值模拟结果通过多元回归分析对预测公式进行修正.并使用另一个模型对修正后的换算公式进行检验,检验结果表明,修正后的换算公式对于预测中比转数离心泵在较小叶轮前盖板平移率时、0.8~1.0倍设计流量工况的扬程变化具有较高的准确度,有一定的工程价值.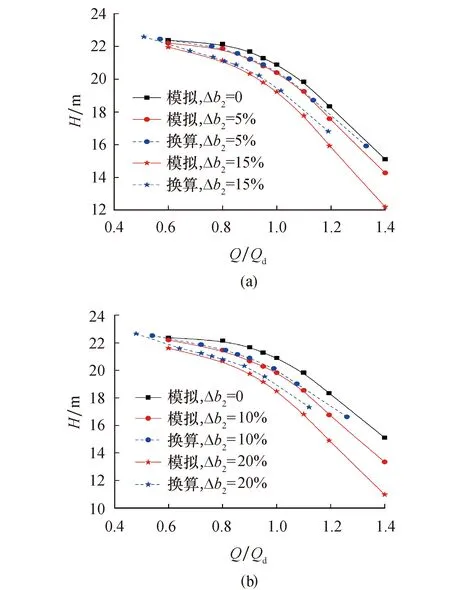
3 结论

