考虑缺口效应的多轴疲劳寿命预估模型
刘俭辉, 潘雪梅, 吕 鑫, 资 绒, 陈晓闯
(1. 兰州理工大学 机电工程学院, 甘肃 兰州 730050; 2. 兰州金川新材料科技股份有限公司, 甘肃 兰州 730101)
在实际应用中工程构件零部件的危险截面处往往承受多轴疲劳载荷作用:一方面,零部件本身承受的外部载荷为多轴复杂载荷;另一方面,出于各种功能性需求,零部件结构日益复杂,构件中往往存在诸多尺寸发生突变的部位,如飞机机翼、涡轮叶片连接处、凸肩,油孔等,这些几何不连续(缺口)部位往往存在着明显的应力集中,进而导致缺口附近的应力场分布不均匀,产生缺口效应[1].具体而言,当缺口根部或表面高应力区材料达到屈服强度并且产生塑性变形时,内层材料由于应力梯度的存在仍处于较低的应力水平,此时,材料内层晶粒对外层高应力区的晶粒起到了一定的支撑作用,从而延缓了疲劳裂纹的形成[2].实际工程应用中,由于缺口效应的存在,即使在单轴外载作用下缺口局部仍呈现出多轴应力应变状态[3-4].在构件的整个服役期内,零部件在多轴载荷作用下,疲劳损伤逐渐累积,导致零件性能不断劣化直至失效.
针对金属缺口件的多轴疲劳寿命预估,目前工程中应用较为广泛的是局部应力应变法,简称LSSA.LSSA假定:若缺口件危险部位受到的局部应力应变历程与作用在相同材料光滑件上的应力应变历程相同,则它们的疲劳寿命相同[5].LSSA采用某些特定的方法(如Neuber法等)计算缺口危险部位的局部应力应变历程,再结合材料相应的疲劳曲线预测构件寿命.此法计算简单,使用也比较广泛,但是它只考虑了缺口热点处的局部应力应变,忽视了多轴效应和缺口附近应力梯度的影响.因此,在缺口局部应力梯度较低时,预测精度相对较好,当存在较大应力梯度时,计算偏差较大,计算结果往往过于保守[6].同时,大量的疲劳寿命分析结果与实验结果对比表明,局部应力应变法在低周疲劳时得到的疲劳寿命总体比较符合,但在中高周疲劳时,疲劳寿命分析结果远低于实验结果[7-8].
局部应力应变法基于大量的实验数据,却忽视了对于基本理论的深入探索.基于实验数据而得到的经验性公式虽然可以应用于工程实际问题,但是对于疲劳问题的长期研究而言,存在一定的盲目性,缺乏系统性.损伤力学基于连续热力学和连续介质力学的基本理论,弥补了LSSA未考虑材料细观结构的缺陷(如微裂纹、微孔洞等)引起材料或结构的劣化过程[9]这一不足,作为传统分析方法的一种补充,为金属疲劳问题的研究开辟了一条新的途径.
Kachanov[10]在研究金属的蠕变断裂时,首次提出关于有效应力和连续因子的概念.20世纪70年代,各国学者相继借助连续介质力学的相关方法,提出将损伤因子作为损伤参量,该损伤参量可以用于描述构件的损伤状态.损伤力学理论认为试件在循环载荷作用下,应力应变场会与损伤场产生耦合,使得损伤场随着载荷的循环而不断发生演化,逐渐产生疲劳裂纹,继而导致疲劳破坏.该方法的核心是根据引入的损伤变量构建损伤演化方程来描述损伤场随载荷循环次数的演化过程,从而通过对方程的求解,得出产生疲劳裂纹时的载荷循环次数,即裂纹形成寿命[11].尚德广等[12]将临界面法与连续介质损伤力学相结合,对等效应变给出了一种新的定义方法,提出了一种非比例加载条件下的多轴疲劳寿命预测方法.Zhang等[13]根据热力学定律,提出了新的损伤演化方程,基于保守积分理论,推导了缺口试样最大应力与疲劳寿命之间的关系,并采用新提出的损伤力学-有限元方法预测了变径连杆的平均疲劳裂纹萌生寿命.Zhan等[14]在ANSYS平台上利用APDL语言,考虑材料的疲劳损伤与结构应力分布之间的耦合效应,预测了试样的疲劳寿命.Shen等[15]通过在ANSYS中进一步开发APDL语言,将疲劳模型集成到FEM中,提出了一种损伤力学有限元方法来预测缺口试样和工程结构的多轴疲劳寿命.李友胜等[16-17]基于损伤力学理论,采用封闭解法,给出了切口构件在拉压载荷下的损伤演化方程,提出了一种缺口构件疲劳裂纹萌生寿命的预测方法.Liu等[18]基于损伤力学和临界面方法,利用已有的实验数据和有限元法分别得到了材料常数和应力集中系数,提出了一种预测在拉-扭耦合作用下几何不连续结构疲劳寿命的新方法.上述基于损伤力学的多轴疲劳计算方法大多借助FEM,其分析结果随网格划分方式及网格形状、大小等的不同存在一定的不稳定性,而且运算量也较大[19].
本文基于损伤力学理论,结合von Mises等效准则的思想,建立一种预估缺口件在多轴载荷作用下疲劳寿命的新模型.新模型不涉及复杂的材料常数,计算简单,仅需通过缺口件的单轴疲劳数据得到相关拟合参数即可预估多轴载荷作用下的疲劳寿命.本文选用3种材料的疲劳实验数据,验证了该模型的准确性和可靠性.
1 损伤本构方程
损伤力学理论认为构件在外载作用下有效承载面积的减少会导致损伤出现,进而导致材料的劣化.为了描述这种损伤,该理论提出了连续度的概念[9].
选取材料的一个微元体,如图1所示,某一面的截面积为A,其法向为n.如果该面上产生微裂纹,则其实际有效的截面积A′要小于A,则认为连续度
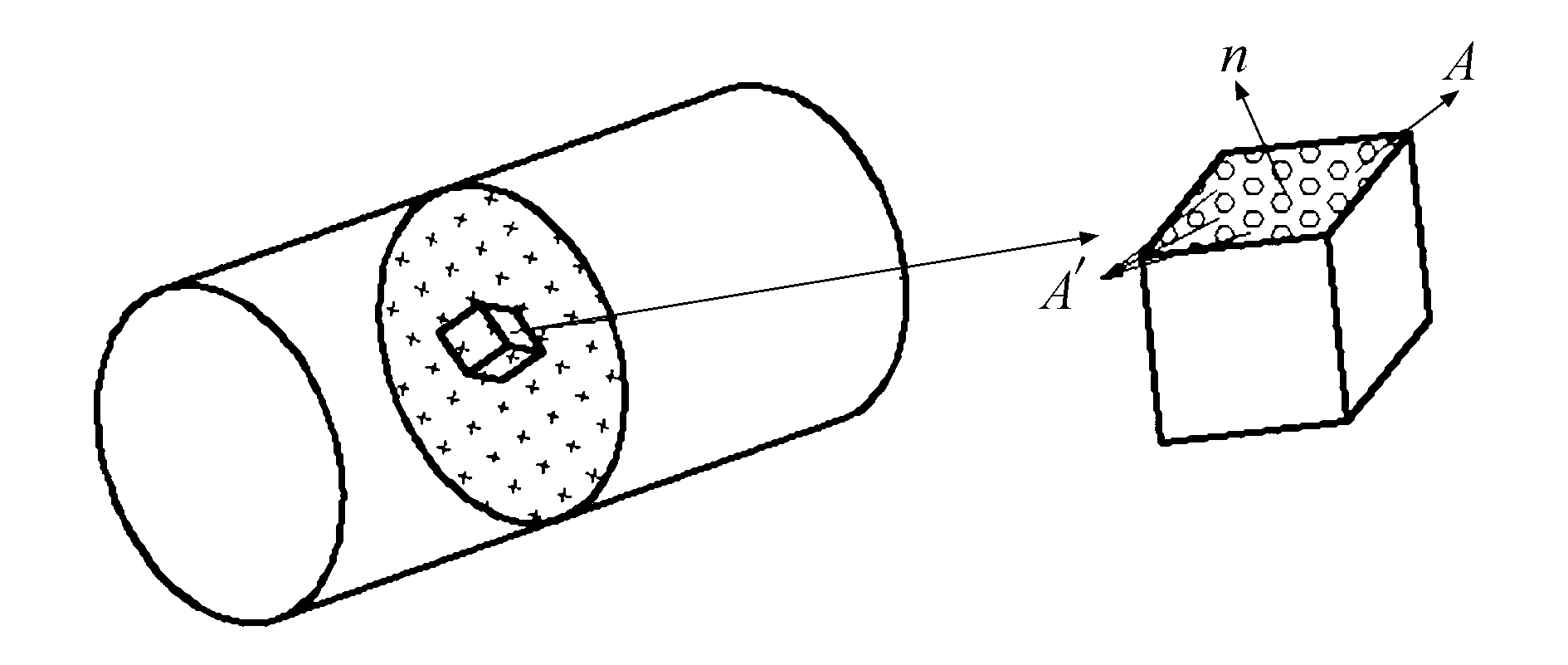
图1 损伤单元
φ=A′/A
(1)
当0≤A′≤A时,0≤φ≤1.
材料性能的退化也可以用循环载荷下刚度的降低来描述.一般采用损伤度[20]的概念来表示刚度的降低,其表达式为
D=1-φ=(A-A′)/A
(2)
式中:D表示损伤度.
由式(2)可以看出,损伤度D能够直接表示材料的损伤.当材料没有损伤,即A′=A时,D=0;当结构失效时,A′=0,此时损伤度D达到最大值1,而在实际工程结构中D一般在未达到1时即发生疲劳破坏.
由式(2)可得到有效截面积A′=(1-D)A,有效应力σ′定义为载荷F与有效承载面积A′之比,即
(3)
式中:σ为缺口处名义应力.
式(3)是损伤变量的经典表达式,已被广泛接受.但是在含损伤材料中,要从细观上对每一种缺陷形式和损伤机制进行分析来确定有效承载面积是很困难的.为了能间接地测定损伤,1971年Lemaitre[21]在Kachanov理论的基础上提出了应变等效假设.该假设认为,受损材料的变形行为可以只通过有效应力来体现,换言之,损伤材料的本构关系可以采用无损时的形式,只要将其中的应力替换为有效应力即可.依据此假设,利用材料的本构关系可以推导出含任意损伤的材料的本构方程,一般情况下的本构关系为
(4)
式中:ε为有效正应变;E为弹性模量.
针对几何不连续构件,缺口会导致应力集中,使缺口根部应力应变增加.考虑缺口处应力集中系数KT的影响,式(4)可表示为
(5)
针对单轴拉伸疲劳失效,Lemaitre和Plumtree[22]建议用式(6)来描述疲劳损伤演化:
(6)
式中:σmax为最大循环正应力;σm为平均正应力;N为应力循环次数;p和β为与温度有关的材料常数;M(σm)是与σm有关的函数,M(σm)=M0(1-tσm),其中,M0为σm=0时的参数.
同样,考虑缺口处应力集中系数KT的影响,式(6)可表示为
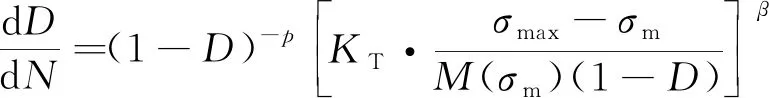
(7)
2 基于损伤演化的疲劳寿命预估模型
对于拉-扭耦合加载下的多轴疲劳试样,von Mises等效应力σeq定义为
σeq=(σ2+3τ2)1/2
(8)
鉴于Lemaitre and Plumtree模型只考虑了单轴拉伸疲劳失效的情况,不适用于多轴疲劳问题.本文基于von Mises等效准则思想,同时考虑拉伸和扭转作用,即正应力和切应力对于构件多轴疲劳失效的共同影响,将式(7)引申到拉-扭耦合加载下的疲劳损伤计算,建立了一个新的多轴疲劳损伤演化方程,即
式中:τmax为最大循环剪应力;τm为平均剪应力;M(τm)是与τm有关的函数,M(τm)=M1(1-tτm),其中,M1为τm=0时的参数,恒幅对称载荷时,M0与M1相等.
对上述损伤演化方程从D=0到D=1进行积分可得如下模型:
(11)
本文研究对称等幅荷载时的疲劳损伤问题,此时,σm=0,τm=0,因此式(11)可以表示为
(12)
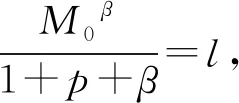
Nf=lKT·a·σmax+3b·τmax-β
(13)
a=1,b=0时,式(13)退化到单轴拉伸状态,即
(14)
a=0,b=1/3时,式(13)退化到单轴扭转状态,即
(15)
式中:a和b的数值可通过所施加载荷计算而得;l和β可利用缺口件的单轴疲劳数据通过拟合得到.
3 实验验证
为验证本文所提出模型的适用性和准确性,从相关文献中选取3种材料的缺口疲劳实验数据进行验证,这3种材料包括GH4169镍基高温合金[23-24]、SAE1045钢[25]和LY12CZ铝合金[26-27].试件所承受载荷均为拉-扭恒幅对称载荷,相位差包括0°、45°和90°.
GH4169镍基高温合金试件为实心圆棒件,在其标距段中心处有一个半径为5 mm、深度为1 mm的环状U型缺口;SAE1045钢试件为实心圆棒,在其标距段中心处有一直径为5 mm、深度沿径向的圆孔;LY12CZ铝合金试件为缺口薄壁圆管试验件,圆管壁厚为1.2 mm,在其标距段中心处有一个半径为1 mm的圆孔.表1为各材料力学性能常数和单轴疲劳材料常数.
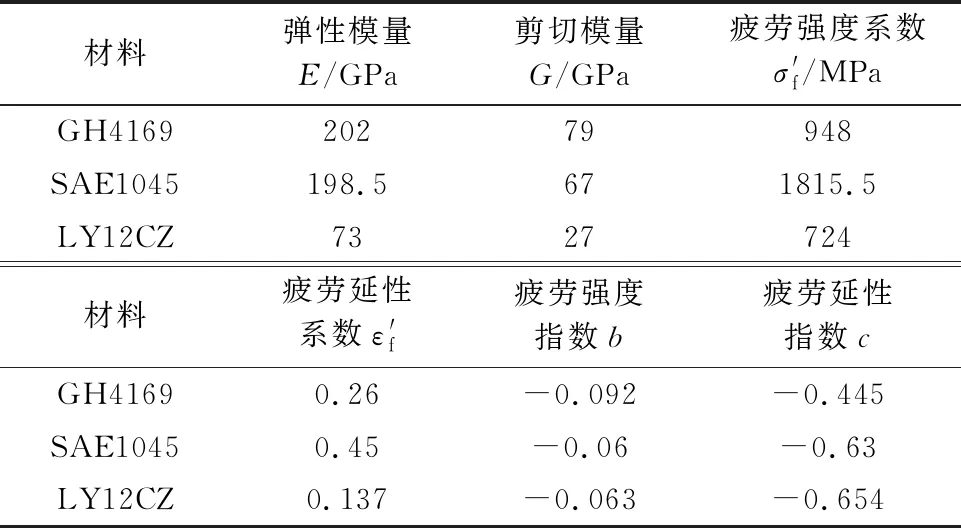
表1 材料力学性能常数和单轴疲劳材料常数
根据3种试件的几何形状和缺口尺寸查询应力集中系数手册[28]得到这3种试件的KT值.同时针对3种材料选取其单轴疲劳数据对l和β进行拟合,所得拟合参数如表2所列.
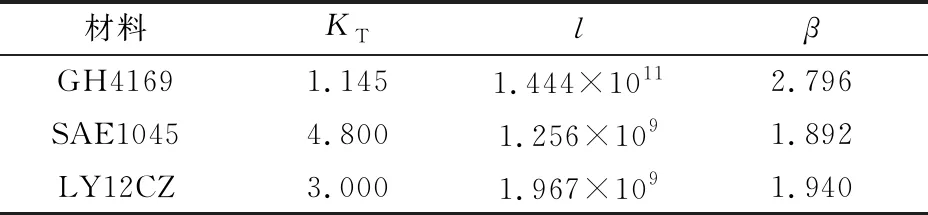
表2 3种试件的应力集中系数及材料的拟合参数
根据拟合参数对3种材料的疲劳寿命进行预测,并与文献中提供的实验寿命进行对比.需要说明的是对于材料SAE1045,文献中给出了每个测试条件下的3组寿命数据,在验证时先利用式(16)得到其中值寿命N50,再进行验证.
(16)
利用该模型预估的寿命与实验数据进行对比,结果如图2所示.
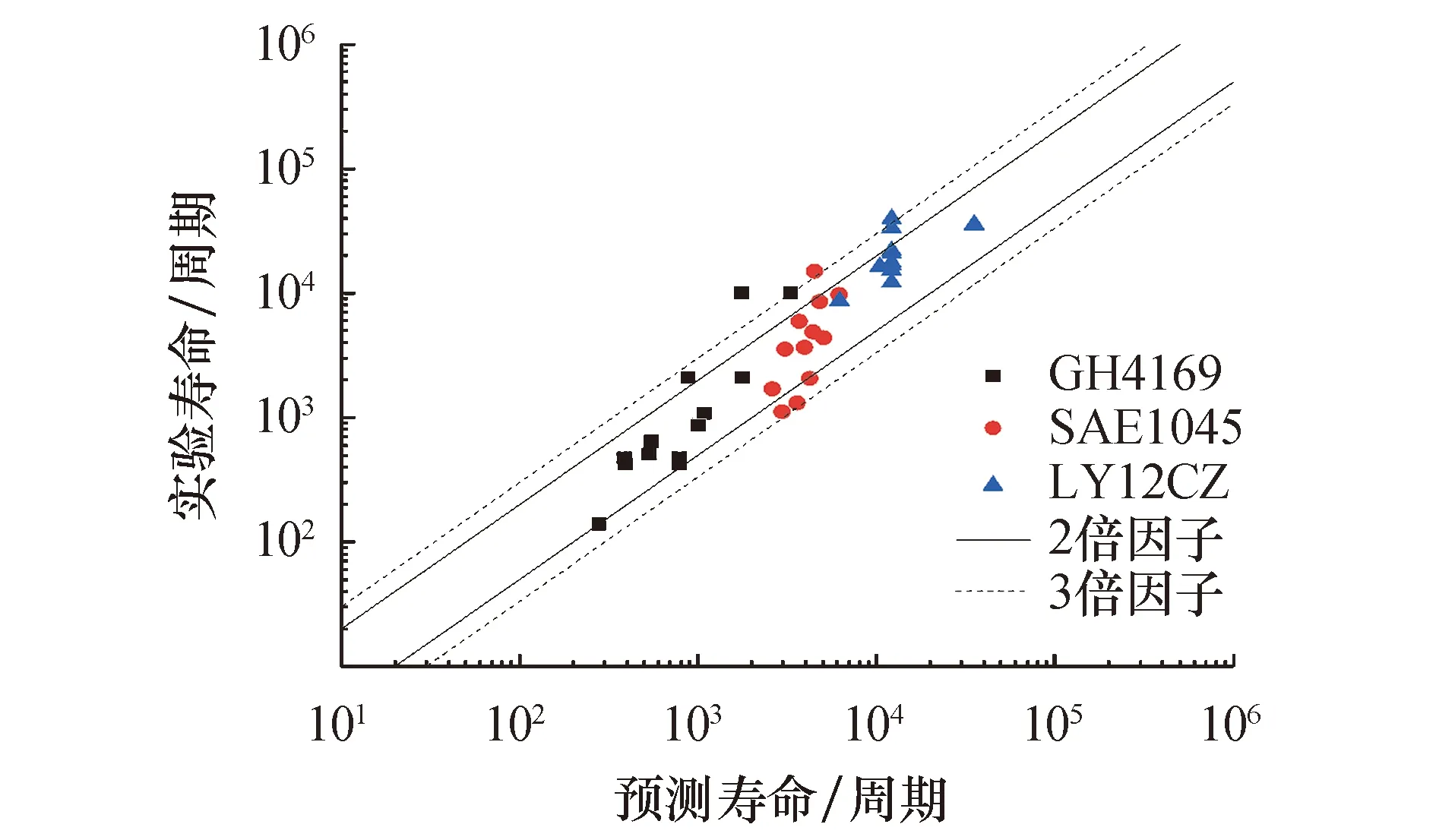
图2 本文模型疲劳寿命预测结果
由图2可以看出,这3种材料的大部分预测结果位于2倍因子分散带之内,个别数据位于3倍因子分散带以外,总体而言,本文模型预测结果良好.
为了进一步说明该模型的准确性,利用局部应力应变法式(17),对3种材料的疲劳寿命进行预测,并与实验结果进行对比,如图3所示.
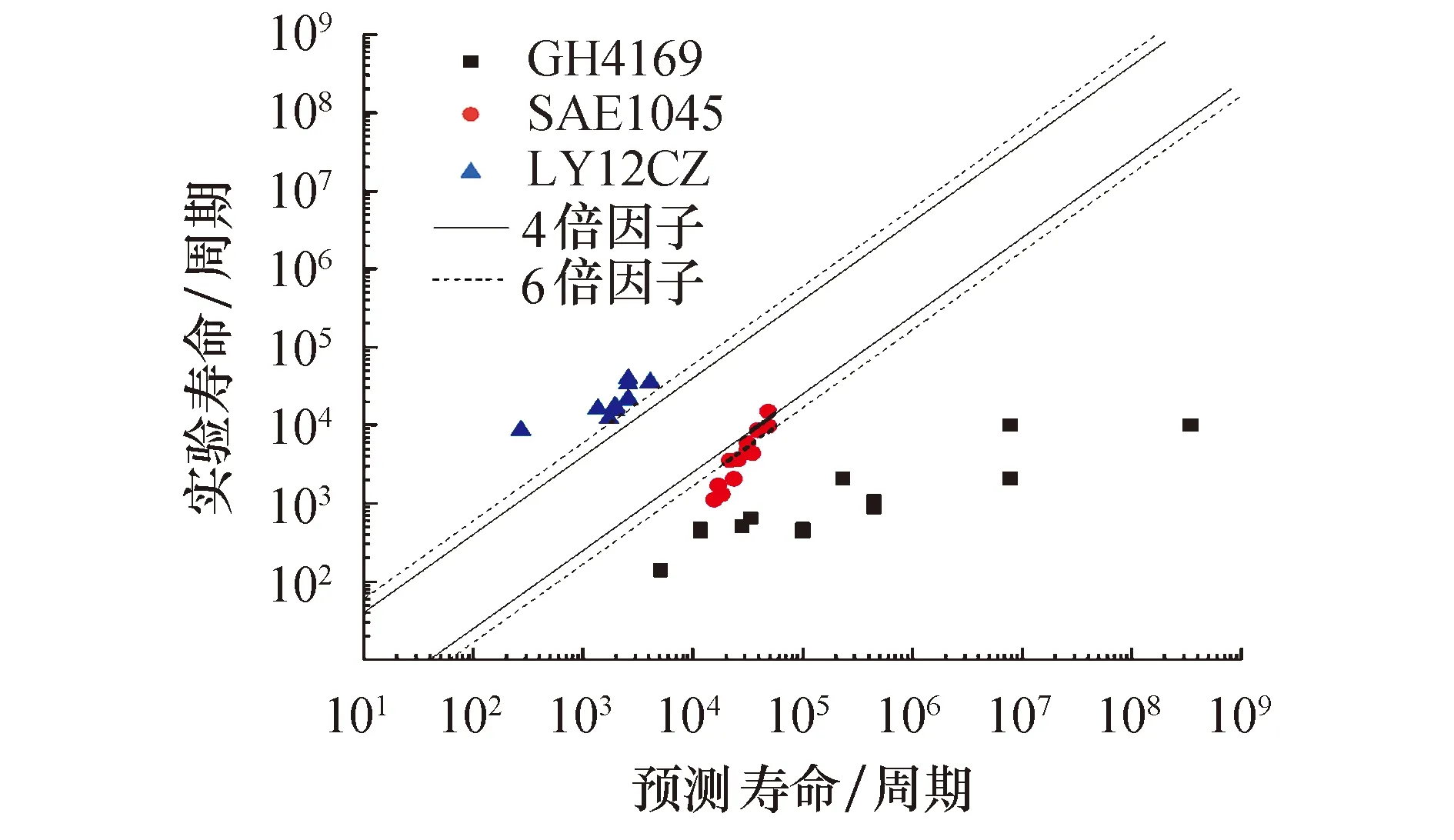
图3 局部应力应变法疲劳寿命预测结果
σLSSA=σmax=f(Nf)
(17)
式中:σLSSA为局部应力应变法所求应力;σmax为缺口处最大正应力.
由图3可以看出,利用局部应力应变法预测所得结果分散性较大,大部分结果位于4倍因子范围以外.
采用误差指标表达式[29]Error=lgNe-lgNp进一步比较两模型的寿命预估精度,其中,Error表示寿命预测误差指标,Ne和Np分别表示实验寿命和预测寿命.根据两模型的预测误差,绘制基于正态分布误差的概率密度函数曲线,如图4所示.
由图4可以看出,与局部应力应变法相比,新模型有较小的预测误差标准差和均值,更接近实验值.
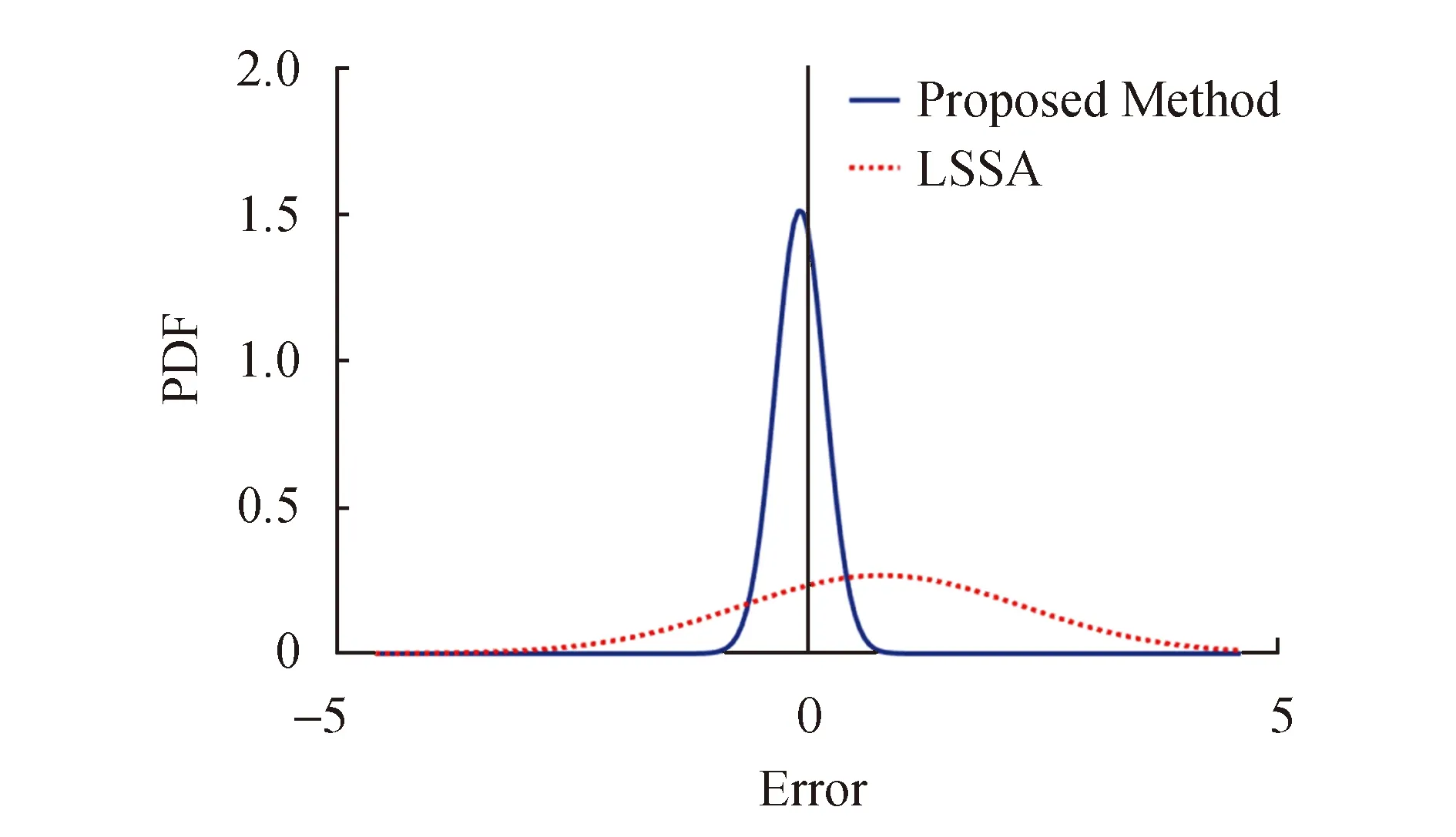
图4 预测误差的概率密度函数曲线
经过在比例和非比例加载条件下验证上述3种材料的多轴疲劳数据,发现该模型比较准确地预测了各级载荷下的疲劳寿命.由此说明,本文提出的模型在预测金属缺口件疲劳寿命时具有较广的适用性和良好的预测效果,其预测精度较传统的局部应力应变法有明显的提高.
4 结论
本文基于损伤力学理论,结合von Mises等效准则的思想,建立了一种适用于金属缺口件的多轴疲劳寿命预估模型.该模型在单轴疲劳寿命模型的基础上,充分考虑了正应力和切应力在多轴疲劳失效中的共同作用,将其引申到多轴疲劳领域.选用3种材料的实验数据对比验证该模型的准确性和可靠性,得到如下结论:
1) 该模型计算简单方便,仅需通过缺口件的单轴疲劳数据拟合参数l和β,即可用于预测多轴载荷下的疲劳寿命.2) 选用3种材料验证该模型的准确性和适用性,显示绝大部分数据在2倍因子范围以内,只有个别数据位于3倍因子范围以外,这可能与实验数据的离散度有关;同时将该模型与传统的局部应力应变法相比较,准确度有明显的提高.
致谢:本文得到兰州理工大学红柳优青资助项目(2020062001)的资助,在此表示感谢.

