一类三阶m点边值问题的三个正解
穆可旺,杨赟瑞,杨 璐
(兰州交通大学 数理学院,甘肃 兰州730070)
三阶常微分方程边值问题在应用数学、物理学涉及的领域应用广泛,例如弯曲梁、重力驱动流等。近年来,越来越多的学者热衷于三阶边值问题正解的研究[1-5],常用方法有度理论、上下解方法和不动点定理等[3-5]。例如,杨春风[6]利用上下解方法研究了一类三阶三点边值问题
两个正解的存在性。2018年,高杨[7]借助锥拉伸与压缩不动点定理建立了三阶m点边值问题
多个正解的存在性。此后,马竹艳等[8]借助Leray-Schauder不动点定理得到了一类三阶m点边值问题正解的存在性。2021年,张瑞燕[9]利用锥拉伸与压缩不动点定理建立了三阶三点边值问题
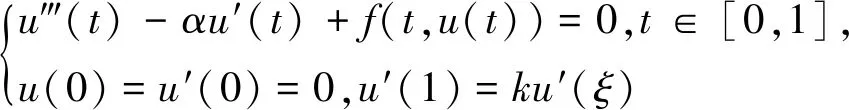
(1)
2m-1(m=1,2,…)个正解的存在性。
受上述工作的启发,本文借助Leggett-Williams不动点定理研究三阶m点边值问题
(2)
三个正解的存在性,其中,α>0,m≥3,ki>0,0<ξi<1,i=1,2,…,m-2。注意到,当m=3时,问题(2)退化为问题(1),因此,本文将张瑞燕一文[9]的研究问题拓展到了m点边值问题,改进并完善了已有多点边值问题正解的存在性研究[4-7]。
1 预备知识
首先给出全文用到的假设条件、相关定义和主要工具:
(H1)f∈C([0,1]×[0,∞);[0,∞))。
定义1[1]设K是实Banach空间X上的一个锥,若映射φ是K→[0,∞)上的连续函数,且当t∈[0,1]时,对任意的x,y∈K,有φ(tx1+(1-t)x2)≥(≤)tφ(x1)+(1-t)φ(x2),则称φ是连续非负的凹(凸)函数。令φ,γ是K中连续非负的凸函数,θ是K中连续非负的凹函数,β是K中连续非负的函数。令a,b,c,d是正常数,定义集合
K(φ,d)={x∈K|φ(x) K(φ,γ,θ,b,c,d)={x∈K|b≤θ(x),γ(x)≤c,φ(x)≤d};L(φ,β,a,d)={x∈K|a≤β(x),φ(x)≤d}。 假设σ1(t)和σ2(t)分别是边值问题 的唯一解。不难得出 显然,σ1(t)在[0,1]上非负且严格递增,σ2(t)在[0,1]上非负且严格递减。 引理1若g(t)∈C[0,1],则边值问题 由文献[9]中的引理2不难验证该结论成立,故省略。 引理2G1(t,s),G(t,s)和σi(t)(i=1,2)具有如下性质: (ⅰ) 对任意的t,s∈[0,1],G1(t,s)≥0; (ⅱ) 对任意的t,s∈[0,1],G(t,s)≥0; (ⅲ) 对任意的t∈[0,1],σ′1(t)>0,σ′2(t)<0,σ″i(t)≥0,σ‴1(t)>0,σ‴2(t)<0,i=1,2; 证明由条件(H2)与G1(t)和G(t)的表达式不难得到(ⅰ)和(ⅱ)成立。而 因此,(ⅲ)成立。由于 则 故(ⅳ)成立。进一步, 因此,(ⅴ)成立。至此,引理2证毕。 由文献[9]中的引理5不难验证该结论成立,故此省略。 因为,对任意的t,s∈[0,1]有G1(t,s)≥0,再结合条件(H1)和(H2)可知, u′(t)≥0, (3) 综上所述,引理4得证。 引理5T:K→K是全连续算子。 证明根据T和K的定义易知T:K→K是连续算子,故仅需证T:K→K是相对紧的。因为对任意的t∈[0,1],u∈K⊂X=C2[0,1],由条件(H1)可知,存在正数M1>0使对任意的t∈[0,1]有f(t,u(t))≤M1。令 结合引理2和引理4可知, 故T在C2[0,1]上一致有界。下证T在C2[0,1]上等度连续。对任意的t1,t2∈[0,1],不妨假设t1 其中,ζ∈(t1,t2),即T在C2[0,1]中是等度连续的,从而T:K→K是相对紧的。因此T:K→K是全连续算子,证毕。 定理2边值问题 (2) 至少有三个正解u1,u2,u3满足 φ(ui)≤d(i=1,2,3),θ(u1)>b,β(u2)>a,θ(u2) (4) 下面依次验证定理1中的条件①~③成立。 结合条件(H4)可得 最后验证定理1中的条件③成立。显然β(0)=0 若u∈L(φ,β,a,d)且β(u)=a,则由引理4和条件(H5)可知, 即条件③成立。则边值问题(2)至少有三个正解u1,u2,u3且满足式(4)。 例1考虑三阶边值问题 (5) 假设a=1,b=2,d=600,通过计算可得 不难验证条件(H1)~(H5)都成立,由定理2可知,边值问题(5)至少有三个正解u1,u2,u3且满足式(4)。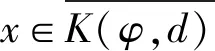
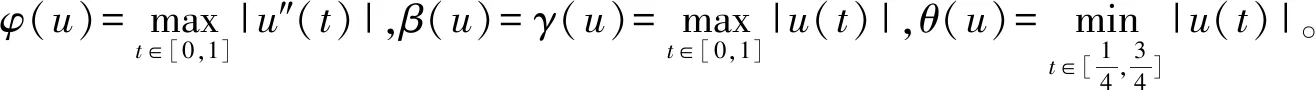
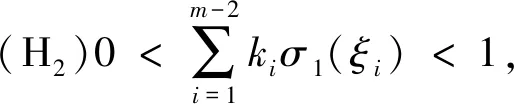
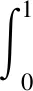
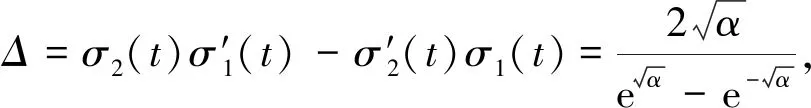
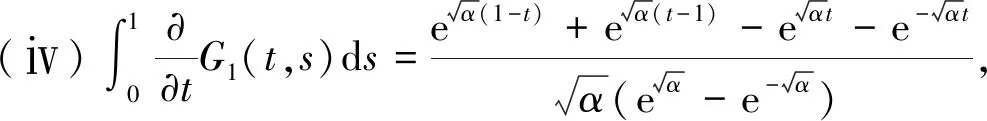
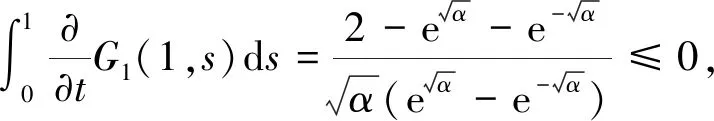
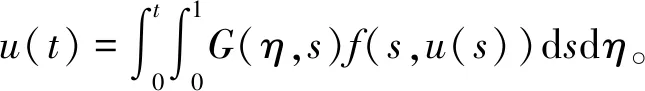
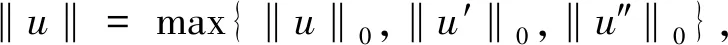
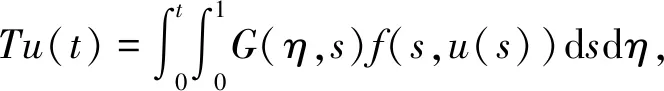
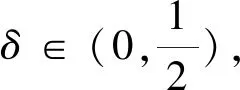
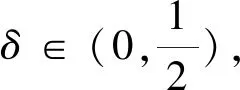
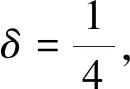
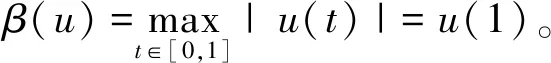
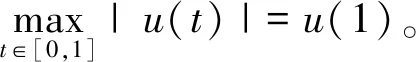

2 主要结论
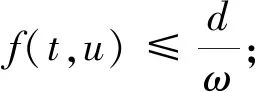
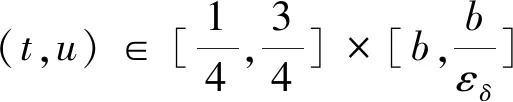
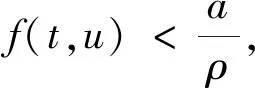
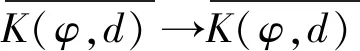

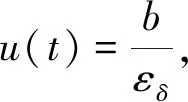
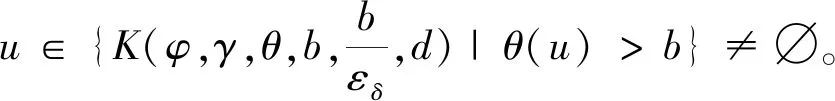
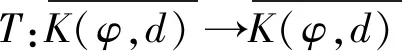
3 应用举例

