后验概率支持向量机模型在目标分类中的应用

米丽萍，邢清华

（1.山西青年职业学院计算机系，山西太原030032；2.空军工程大学防空反导学院，陕西西安710051）

0 引 言

为了解决传统支持向量机［1］（support vector machine，SVM）在不确定分类问题中不能输出后验概率的缺陷［2，3］，Wahba和Platt最先将后验概率运用于SVM方法中，来扩展传统SVM的能力［4，5］。常用贝叶斯框架理论或直接拟合后验概率而不计算类概率密度等方法来确定后验概率，这些都是在传统SVM中引入后验概率的有益尝试［6，7］。本文提出一种基于相对交叉熵的后验概率SVM建模方法，给出了分类问题中交叉熵与相对交叉熵的确定方法，以相对交叉熵最小化作为优化模型的目标函数，建立相应的优化模型，并对优化模型求解，以获得最优的概率SVM模型参数。该方法中，每个支持向量机给出的分类结果采用后验概率的方式确定样本的类别，使样本分类可以得到定性和定量的解释和评价。

1 支持向量机后验概率模型的确定

传统SVM的标准输出为［8］

其中:f（x）＝（w＊×x）＋b＊，w＊与b＊分别为最优分类面的权系数向量和分类的域值。

任意样本点x与分类面之间的距离可以表示为:rx＝

由此得到

对于SVM的分类，如图1所示，从超平面的几何角度分析，样本在两类分类问题中属于其中哪一类的程度更大是通过样本与最优分类面间的距离确定的，而f（x）是rx与rsv的比率，于是样本的后验概率可以依据SVM的标准输出f（x）来度量，因此，后验概率模型可以看成是f（x）的函数。

图1 最优分类面相对位置

概率输出函数需要满足两个条件，一是函数的取值范围必须是［0，1］区间；二是必须为单调函数。通过对能够作为概率输出函数的几种单调函数的分析发现，含有参数A和B的sigmoid函数对SVM的输出概率建模具有更大地灵活性，实际应用时也能够呈现出很好的分类精度，因此后验概率模型可以采用含A、B两个参数的sigmoid函数来确定。

对于两类分类问题，如果采用含参数A、B的sigmoid函数，其SVM的概率输出可以表示为如下形式

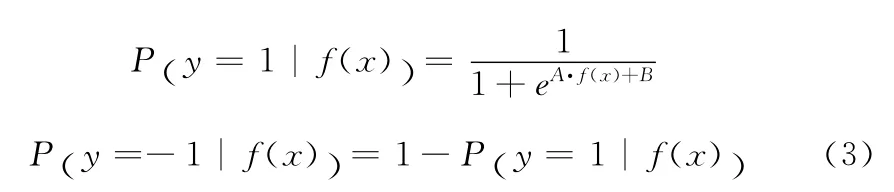
其中:sigmoid函数的形态用参数A和B控制；SVM中样本x的标准输出值用f（x）表示。基于此，如果利用传统SVM概率建模的话，样本x的类别可以根据式子（3）确定，而样本隶属于所在类的程度大小由后验概率的大小来体现，对于传统SVM方法，可以通过式（1）中y＝1或y＝－1来确定样本x的类别。

2 基于相对交叉熵的后验概率SVM模型参数确定方法

可以通过SVM的标准输出f（x）来建立sigmoid函数的后验概率模型，那么接下来如何确定概率模型中的A和B这两个参数呢？这里提出采用最小化相对交叉熵方法来确定概率模型（3）的参数。

2.1 分类问题中交叉熵与相对交叉熵的确定

设随机变量x服从某一未知分布p（x），且该未知分布p（x）可由一已知分布（如某种参数模型）q（x）表示。q（x）与p（x）间的交叉熵（cross entropy）定义为

只有当参数模型q（x）等于p（x）时，交叉熵才可以取得最小值。

针对两类分类问题，假设y＝p（c1｜x），1－y＝p（c2｜x），即若x属于c1时应该得到t＝1的输出，若x属于c2时应得到t＝0的输出，于是

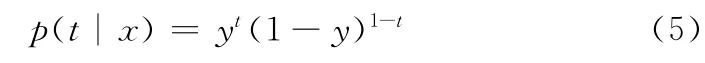
可见p（t｜x）服从Bernoulli分布，若训练样本（xi，ti）（i＝1，2，…，n）是独立选取的，则其似然函数可写为即

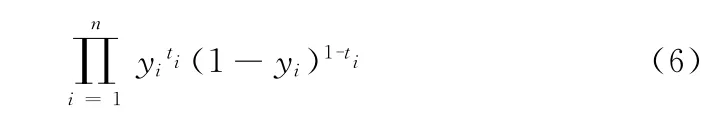
该式取负对数后有

可以证明这就是y（x）与目标t的分布间的交叉熵

如果把yi＝ti代入式（7），可得E1的最小值为

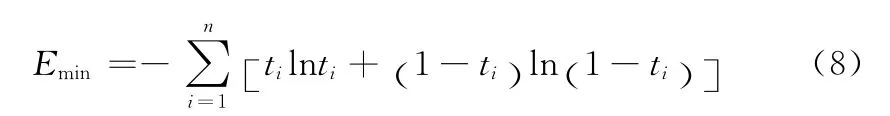
对于两类问题中ti取1或0的情况，Emin＝0，对于ti取（0，1）间连续值的情况，Emin≠0，因此我们可以从式（7）减去式（8），得到一种误差函数形式为

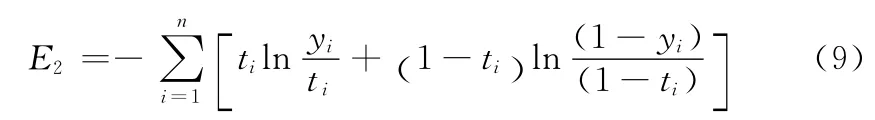
该误差函数实质上是实际输出yi与应有输出ti的相对熵，我们把它叫做相对交叉熵，误差越小，E1与Emin越接近，同时y（x）与目标t越接近。

2.2 基于相对交叉熵最小化的SVM概率模型参数确定方法

有了上面的准备工作，我们设训练样本集（xi，yi）（i＝1，2，…，n）为SVM的训练样本，将另一组样本（fi，yi）（fi＝f（xi））（i＝1，2，…，n）作为训练样本，以求取参数A、B，f（xi）表示SVM的标准输出值，yi∈｛－1，1｝。

在原始数据集中加入噪声，可以避免对Sigmoid函数采用小数据集拟合时出现的过拟合现象，也就是说在重构的训练样本集中，f（xi）为正样本的SVM输出值，正样本对应的目标值为ti＝1－ε＋，而负样本对应的目标值为ti＝ε－，采用Bayes后验概率估计和可以得到一组重新定义的训练样本（fi，ti）（i＝1，2，…，n），其中ti为加入噪声后，f（xi）对应的目标值。具体表达如下

为确定模型pi，需求出表达式pi中的参数A和B的值，使pi与ti的值尽可能地接近，建立pi与ti的相对交叉熵函数为

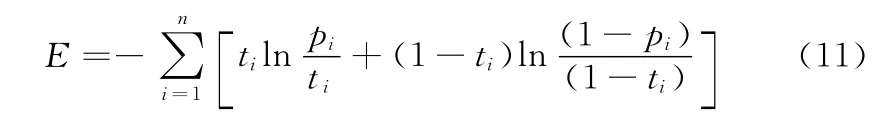
最小化相对交叉熵，可以求得sigmoid函数中的参数A、B。若用向量Z＝（A，B）T来表示求解出的A和B两个参数，则可以得到下面的公式

利用逆向线性搜索特点的牛顿迭代方法，对上式求解参数A和B。

2.3 迭代求解算法的基本思想

对参数A和B的求解。采用迭代求解算法，其基本思想如下:

第一:求F（Z）的梯度▽F（Z）和F（Z）的Hessian矩阵G（Z），其表达式如下

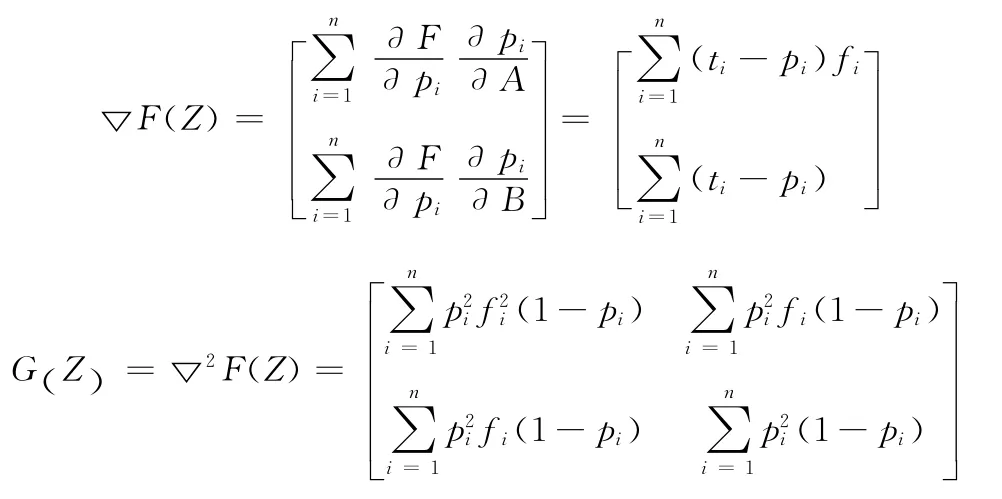
给定初始点Z0，参数σ≥0，以使得H（Z0）＋σI是正定的。

第二:我们将上述问题的求解转换为下式的迭代求解式

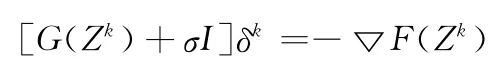
若F（Zk）＝0，则求解结束；

否则αk依次从序列1，…中取值，满足F（Zk＋αkδk）≤F（Zk）＋0.0001·αk（F（Zk）Tδk）的序列中的第一个元素作为αk。设Zk＋1＝Zk＋αkδk，继续迭代。

这样，通过迭代求解，即可得到A、B的值，从而根据式（3）计算出样本x属于某类的后验概率。

2.4 实验分析

为了检验后验概率SVM模型的合理性，采用heart＿scale、ionosphere＿scale、liver－disorders＿scale和ijcnn1数据，进行概率支持向量机的实验，heart＿scale样本总数为300个，其中正样本140，负样本160个，数据特征维数是13；ionosphere＿scale样本个数为360个，其中正样本数是220个，负样本数140个，数据特征维数是34；liver－disorders＿scale样本总数为350，其中正样本155个，负样本195个，数据特征维数是6；ijcnn1实验将训练样本与测试样本相分离，训练样本35022个，测试样本91803个，数据特征维数为22。表1列出了利用相对交叉熵最小化的概率建模方法和利用标准支持向量机方法进行数据分类的结果。

由表1可以看出，采用后验概率SVM的分类效果显然比传统SVM的分类效果好。

3 多类分类中的后验概率SVM模型

3.1 多类分类器设计

上面给出的是一个两类分类问题的后验概率建模方法，实际的分类问题更多的是多类分类问题，对于多类分类的问题，文献［9－11］等采用了计算比较复杂的集成学习方法，本文采用“一对一”的分类方法，先构造M（M－1）/2个两类后验概率SVM分类器，再综合利用M（M－1）/2个两类后验概率分类器计算后验概率，最后利用得到的后验概率来确定在每个分类中样本的最终后验概率。其示意图如图2所示。

表1 利用不同方法进行样本分类的分类正确率

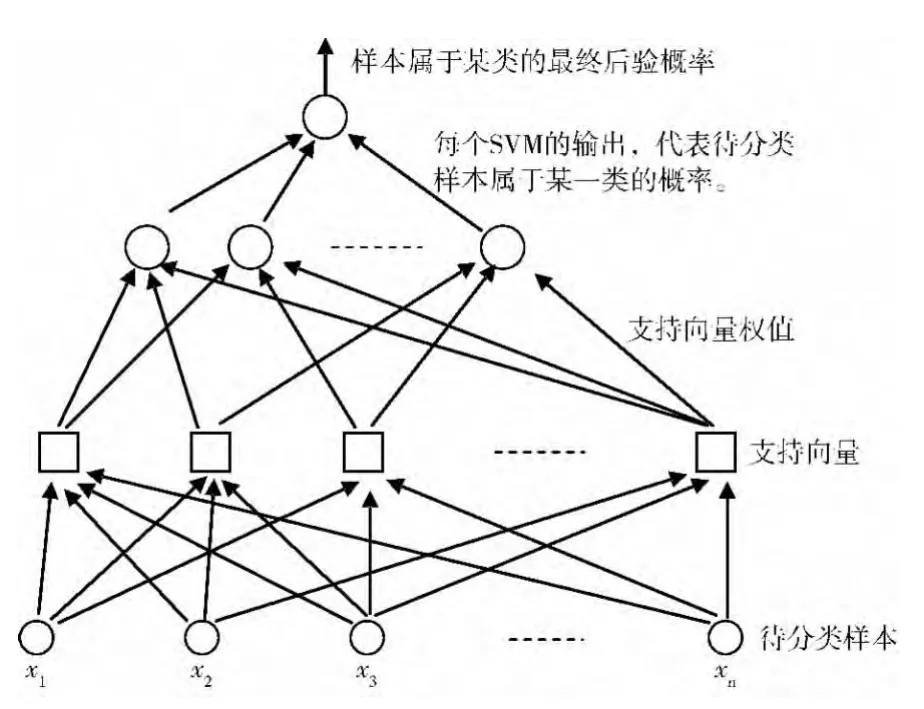
图2 多个分类器组合求解最终后验概率

测试样本x属于第Ci类的最终后验概率计算如下

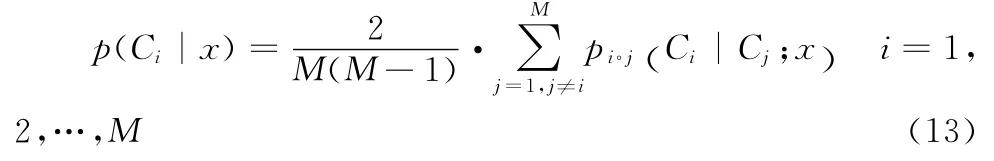
3.2 多类分类仿真实验

以空中目标分类为例，依据分类原则［12］给出目标特征向量分布参数见表2。

为了测试模型，这里针对每类目标生成50个训练样本和6个测试样本，针对5类目标共生成训练样本250个（简称为样本A），测试样本30个（简称为样本B）。

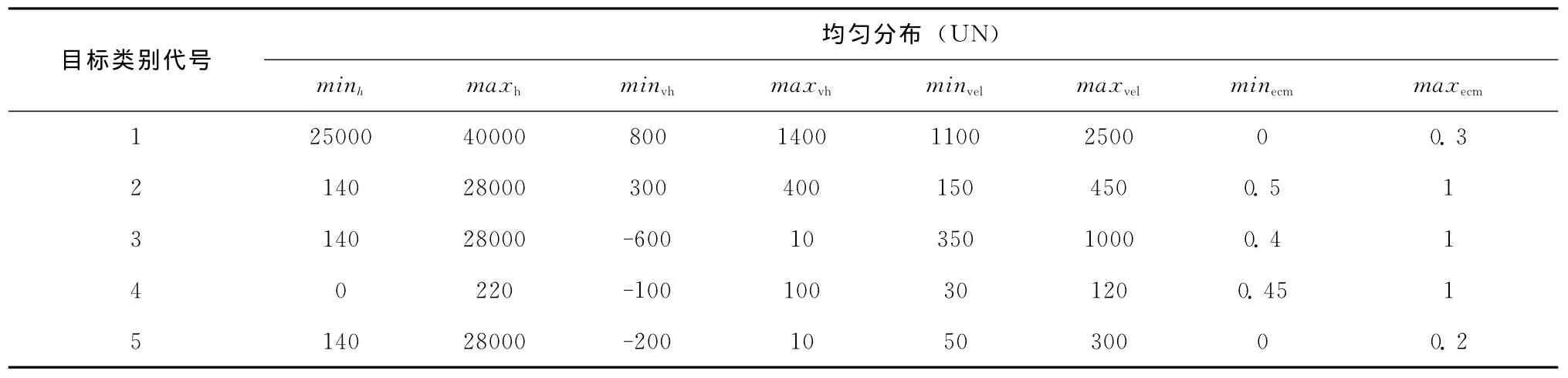
表2 样本A的特征向量分布

目标类别代号与目标类别名称对照具体见表3所示。

表3 目标类别的代号名称对应表

下面给出样本B中每个测试样本所属类别的后验概率计算过程:

首先:将样本A中的训练样本进行归一化处理，并以此为基础，利用径向基核函数对上节中的支持向量机进行训练，得到10个两类后验概率支持向量机中每个分类器模型中参数A、B的值。具体值的列表略。

然后:将样本B归一化后得到的样本作为测试样本集对训练得到的模型进行测试，并利用上节（13）式的多类分类器模型计算后验概率值，得到如表4所示的后验概率及目标的所属类别。

从表4数据可以看出，对于测试样本B，后验概率SVM模型对它的识别率是96.7%，然而采用文献［13］方法，对其识别率只有76.7%。

4 结束语

在目标分类问题中，分类结果经常需以后验概率的形式输出，而传统SVM方法不能满足这一要求，本文从交叉熵的角度，采用相对交叉熵最小化的方法，建立后验概率SVM模型，给出了具有逆向线性搜索特点的牛顿迭代方法求解后验概率SVM模型参数的方法。该方法不但使SVM的分类正确率得到了改善，而且能给出样本所属类别的量度。在此基础上设计了基于后验概率SVM的多类分类器，并应用于空中目标分类，实验结果表明，后验概率支持向量机可以有效提高分类正确率。

表4 多类别分类中目标的后验概率值及其所属类别

3 0.00413558 0.0133134 0.981796 0.000421501 0.000333325 3 4 0.00353095 0.127527 0.0225832 0.845818 0.000541004 4 5 0.010623 0.0106912 0.0152331 0.00272993 0.960723 5 1 0.969591 0.00559093 0.0166665 0.00381363 0.00433755 1 2 0.00293516 0.672011 0.323081 0.000696744 0.001276 2 3 0.00381991 0.000753352 0.991478 0.000686705 0.0032617 3 4 0.00781341 0.0803295 0.0369331 0.814962 0.0599624 4 5 0.00598957 0.00591069 0.0103939 0.00213264 0.975573 5 1 0.973356 0.00452927 0.013324 0.00311687 0.00567392 1 2 0.00934335 0.948051 0.0187119 0.0111845 0.0127093 2 3 0.00333391 0.0793888 0.576721 0.337717 0.00283915 3 4 0.00436924 0.0789715 0.0161308 0.898253 0.00227517 4 5 0.0196133 0.00909373 0.0163751 0.00255307 0.952365 5 1 0.970823 0.00606837 0.00600331 0.00235171 0.0147534 1 2 0.00737461 0.973206 0.00794391 0.00182058 0.0096545 2 3 0.0105619 0.00568334 0.956984 0.0025174 0.0242538 3 4 0.00586149 0.0698278 0.0212333 0.887497 0.0155806 4 5 0.00757814 0.00965415 0.0225287 0.00381244 0.956427 5 1 0.951522 0.0173767 0.00536047 0.00562711 0.0201137 1 2 0.00207347 0.992592 0.00217638 0.00278346 0.000375063 2 3 0.00319638 0.067679 0.928009 0.000638311 0.000477201 3 4 0.00624763 0.0458183 0.0694339 0.80692 0.0715799 4 5 0.00554806 0.0277235 0.0450976 0.168463 0.753168 5 1 0.940864 0.0268203 0.00742096 0.00461744 0.020277 1 4 0.00470158 0.23067 0.27119 0.49006 0.00337813 2 3 0.00337171 0.026324 0.963727 0.00557892 0.000998284 3 4 0.00382561 0.093183 0.0157115 0.886434 0.000845728 4 5 0.00379318 0.0128395 0.0420917 0.0145445 0.926731 5

［1］WEN Chuanjun，ZHAN Yongzhao，CHEN Changjun.Maximal－margin minimal－volume hypersphere support vector machine［J］.Control and Decision，2010，25（1）:79－83（in Chinese）.［文传军，詹永照，陈长军.最大间隔最小体积球形支持向量机［J］.控制与决策，2010，25（1）:79－83.］

［2］SHEN Juhong，HUANG Yongdong.Fuzzy support vector machine based on possibility measure［J］.Journal of Natural Science of Heilongjiang University，2012，29（2）:204－206（in Chinese）.［沈菊红，黄永东.一种可能性测度的模糊支持向量机［J］.黑龙江大学自然科学学报，2012，29（2）:204－206.］

［3］SU Zhan，XIU Lixia.Review on support vector machine based on bayes theorem［J］.Computer Applications and Software，2010，27（5）:179－181（in Chinese）.［苏展，徐丽霞.基于贝叶斯理论的支持向量机综述［J］.计算机应用与软件，2010，27（5）:179－181.］

［4］ZHANG Xiang，XIAO Xiaoling，XU Guangyou.Weighted posterior probability output for support vector machines［J］.Journal of Tsinghua University（Natural Science），2007，47（10）:1689－1691（in Chinese）.［张翔，肖小玲，徐光祐.支持向量机方法中加权后验概率建模方法［J］.清华大学学报（自然科学版），2007，47（10）:1689－1691.］

［5］LI Yongli，LIU Yanheng，XIAO Jiantao，et al.Incremental learning algorithm based on support vector machine［J］.Journal of Jilin University（Science Edition），2010，48（3）:464－467（in Chinese）.［李永丽，刘衍珩，肖见涛，等.基于支持向量机的增量学习算法［J］.吉林大学学报（理学版），2010，48（3）:464－467.］

［6］HU Wenliang，WANG Huiwen.Prediction modeling based on Bayes support vector machine［J］.Journal of Beijing University of Aeronautics and Astronautics，2010，36（4）:486－489（in Chinese）.［呼文亮，王惠文.基于贝叶斯准则的支持向量机预测模型［J］.北京航空航天大学学报，2010，36（4）:486－489.］

［7］ZHAO Chunjie，WANG Shuxun.Research of support vector machine in the primal［J］.Journal of Shanxi University of Technology（Natural Science Edition），2010，26（2）:58－64（in Chinese）.［赵春婕，王树勋.支持向量机原始问题研究综述［J］.陕西理工学院学报（自然科学版），2010，26（2）:58－64.］

［8］YANG Zhiming，LIU Guangli.Principle and application of uncertainty support vector machines［M］.Beijing:Science Press，2007:32－51（in Chinese）.［杨志明，刘广利.不确定性支持向量机原理及应用［M］.北京:科学出版社，2007:32－51.］

［9］ZHANG Shuning，WANG Fuli，YOU Fuqiang，et al.Robust least squares support vector machine based on robust learning algorithm and its application［J］.Control and Decision，2010，25（8）:1169－1172（in Chinese）.［张淑宁，王福利，尤富强，等.基于鲁棒学习的最小二乘支持向量机及其应用［J］.控制与决策，2010，25（8）:1169－1172.］

［10］Mao Shasha，Jiao Licheng，Xiong Lin，et al.Greedy optimization classifiers ensemble based on diversity［J］.Pattern Recognition，2011，44（6）:1245－1261.

［11］Li Ye，Cai Yunze，Yin Rupo，et al.Support vector machine ensemble based on evidence theory for multi－class classification［J］.Journal of Computer Research and Development，2008，45（4）:571－578（in Chinese）.［李烨，蔡云泽，尹汝泼，等.基于证据理论的多类分类支持向量机集成［J］.计算机研究与发展，2008，45（4）:571－578.］

［12］Indrajit Saha，Ujjwal Maulik，Sanghamitra Bandyopadhyay，et al.SVMeFC:SVM ensemble fuzzy clustering for satellite image segmentation［J］.IEEE Geoscience and Remote Sensing Letters，2012，9（1）:52－55.

［13］XING Qinghua，LIU Fuxian，WANG Lei，et al.On air targets recognition based on probability support vector machines［C］//Proceedings of the 30th Chinese Control Conference，2011:3239－3242（in Chinese）.［邢清华，刘付显，王磊，等.基于概率支持向量机的空中目标识别研究［C］//中国自动化学会控制理论专业委员会D卷（中国会议），2011:3239－3242.］