去除高斯噪声的快速分区域去噪算法
杨先凤,樊 勇,彭 博,陈 琳,王奥民
(西南石油大学计算机科学学院,四川成都610500)
0 引 言
数字图像在获取和传输过程中常常会受到噪声的污染,从而导致图像质量下降。能否有效且快速地去除噪声对某些后续处理来说至关重要。
到目前为止,学者已对图像噪声做了大量的研究,并提出了相关模型及去噪算法。如,基于小波理论的阈值收缩去噪法、基于脉冲耦合神经网络的PCNN图像去噪、基于统计理论的图像去噪、基于偏微分方程的图像去噪等等[1-9]。这些方法中,分区域去噪算法由于能根据图像的局部特征分别采取不同的方法进行滤波,因而效果较好。但是该方法存在:人为地选定区域划分的阈值、整个去噪过程耗时较多的问题。为了解决这两个问题,本文提出了一种新的快速分区域去噪算法。该算法不仅有效地解决了上述两个问题,而且去噪后的图像在较好地保留了图像边缘细节信息的同时,还有较高的峰值信噪比。
1 传统分区域去噪算法
传统分区域去噪算法的一般步骤是:首先进行区域划分,然后对不同的区域分别采取不同的策略进行去噪,最后合成恢复图像。其中区域划分有较多的策略可以采取,如阈值分割法、基于边缘的方法、基于区域的方法以及基于特征的方法等。
文献[10]提出了一种分区域去噪算法,该算法的步骤是:
步骤2 计算图像像素点f(i,j)某一领域的标准差σi,j;
步骤3 设定阈值e1,e2;根据σi,j-与e1、e2的关系把图像换分成平滑区域、突变区域和过渡区域;
步骤4 分别对图像的不同区域用具有平移不变性的离散小波变换DWT和NeighShrink_Sure方法去噪,最后再合成图像。
该算法取得了很好的处理效果,但是存在以下问题:
(1)阈值参数e1,e2的选取范围过大,e1∈(2,5),e2∈(8,13);合成时还有参数α,β需要选择。整个过程存在较多的人为因素,增加了处理结果的不确定性因素。
(2)局部标准差的计算和基于Sure的NeighShrink算法耗时较多,从而导致整个算法处理时间过长。限制了其应用范围。
2 快速分区域去噪算法
针对文献[10]中所代表的问题,本文提出了一种新的分区去噪算法,主要创新点有:
(1)去掉阈值参数的人为因素:图像分区域时,采用边缘检测方法,仅用一个确定的阈值,但却可以实现很好地划分,避免了结果的不确定性。
(2)减少了标准差的计算时间:对局部标准差的计算进行了优化,成倍地缩小了用统计方法进行区域划分的时间。
(3)替换了耗时的NeighShrink_Sure算法:用具有代表边缘信息的特征值进行边缘区域灰度值的重构。在保留图像轮廓细节的同时,提高了整个程序的运行速度。
2.1 区域划分
由于图像在平滑区域存在着相似性,在边缘区域存在着突变。这种性质导致了图像灰度值在平滑区域的标准差较小,但在边缘区域的标准差较大这一现象。设原始图像S的大小为row×col,加性白高斯噪声为N,污染图像为F,则有
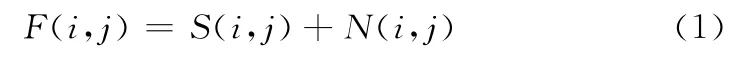
其中,1≤i≤row,1≤j≤col。由于S与N相互独立,所以方差间有以下公式

同样在灰度值F(i,j)的某个领域范围内(如,5x5邻域等)的方差有公式
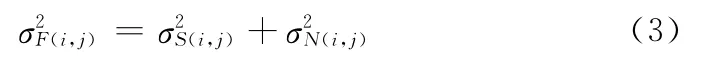
所以由式(3)可得
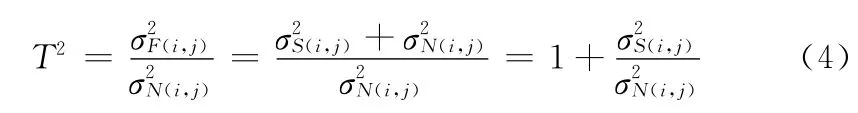
从上面的分析中知道,只要设定合适的阈值就可以划分出平滑区域和边缘区域。根据大量的实验结果和四舍五入原则,本文的区域划分公式为
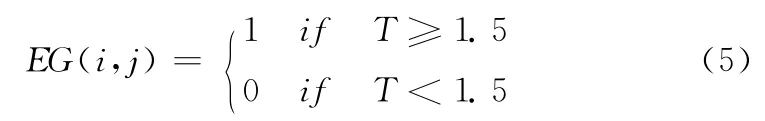
式(5)中,当EG(i,j)=1时,表示像素点F(i,j)位于边缘区域;EG(i,j)=0时,F(i,j)在平滑区域。
由于噪声N未知,所以式(4)中σN(i,j)不能求得,在文献[11]的基础上用

其中,作为噪声N的估计,MF为F均值滤波的结果,式(4)中的σN(i,j)就可以用σ^N(i,j)来替换。于是,根据式(4)和式(6)有T的计算式

根据上面所述,得到本文的区域划分算法:
步骤1 按式(6)进行噪声估计;
步骤2 在F(i,j)的5x5邻域内,按式(7)计算T;
步骤3 根据式(5)把污染图像F进行区域划分;
步骤4 去除矩阵EG中的孤立0点和1点。
不同噪声下Lena图像区域划分效果如图1、图2所示。

图1 σ=8时,不同算法的划分效果

图2 σ=20时,不同算法的划分效果
从图1、图2(d)和图2(a)、图2(b)的对比可以看到本文分区域算法有较强的抗噪能力;从图1图2中(d)和(c)的对比可以看到本文分区域算法有较强的检测弱边缘的能力。
区域划分的时间优化:在计算F(i,j)的5x5邻域内标准差时,如果直接按式(8)计算,区域划分将耗时很大
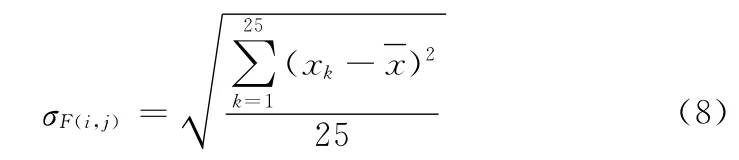
其中,xk为像素点F(i,j)的5x5邻域内灰度值,为邻域内所有灰度值xk的均值,k=1,2,3…,25。
为了缩短运行时间,把式(8)变形为式(9)的形式后,可以显著提高运行速度
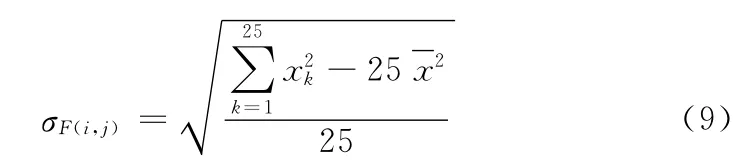
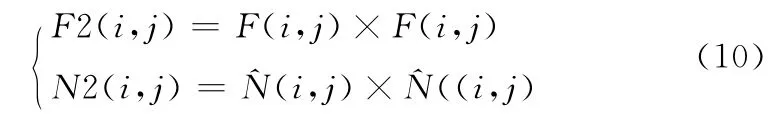
如果用yk来表示F 2和N 2矩阵的元素值,则式(9)变为如下形式
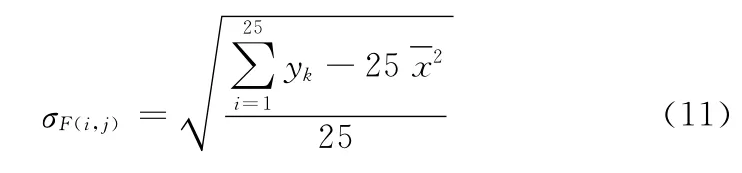
这样在计算σF(i,j)时,yk从F 2矩阵中直接读取;计算σ^N(i,j)时yk从N 2中读取。
由于F2和N2只需计算一次,此后就可以直接读取。因此它们避免了在算局部标准差时需要重复计算的问题,可以大大加快程序运行的速度。表1为不同公式进行区域划分的耗时,展现了其效果。
从表1可看到本文用式(11)进行区域划分所耗的时间,是采用式(8)(或式(9))的几百分之一(或五分之一左右)。极大地提高了程序的运行速度。
2.2 分区域去噪
由于图像自身的特点,在边缘区域里灰度值的相似性具有方向性,如图3所示。但是在平滑区域的的灰度值则是各向同性的。这些边缘区域通常是由局部、轮廓、点要素等构成[12],因此边缘区域的灰度值可由表征这3类信息的灰度值重构。

表1 不同公式进行区域划分的耗时
2.2.1 平滑区域去噪
在速度较快的算法中:当噪声较强时,均值滤波效果较好;而在噪声较弱时,维拉滤波效果较好。因此本文提出了平滑区域的灰度值重构算法
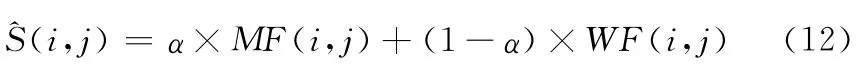
式中:MF——F的均值滤波结果;WF——F的维纳滤波结果;α的计算按式(13)
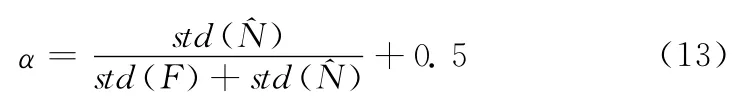
2.2.2 边缘区域去噪
文献[10]中基于SURE的NeighShrink算法虽然能很好地保留边缘区域的细节,但是由于要寻找子带的最优邻域窗口和阈值,因此程序运行时间较长。采用基于SURE的NeighShrink去噪算法运算时间见表2。在某些把去噪作为预处理阶段的应用场合中,这样的算法就不合适。因此有必要在边缘区域采取其它的去噪算法。
文献[13]指出了边缘区域的重构算法,但是算法过于复杂。因此本文采用了文献[12]中的局部、轮廓、点等要素来重构边缘区域的灰度值。
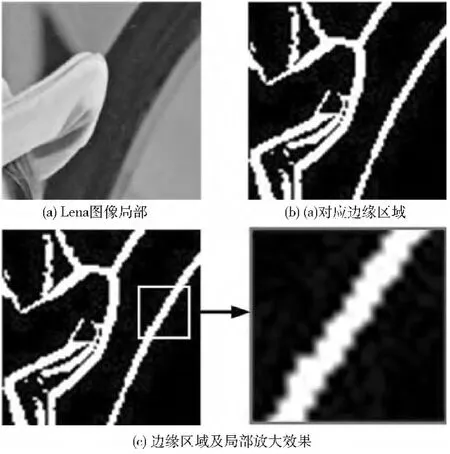
图3 边缘区域局部
首先是表征局部信息的灰度值重构。设3x3窗口内所有灰度值组成的集合为A3={xk},k=1,2,3,4,5,6,7,8,9。其均值为μA3,标准差为σA3。则={xk|,k=1,2,3,4,5,6,7,8,9。这里采用改进型的均值法,是因为其可以剔除掉局部区域一些异常的数据,而保留主要成分。然后再用式(14)重构代表局部要素的^S(i,j)A
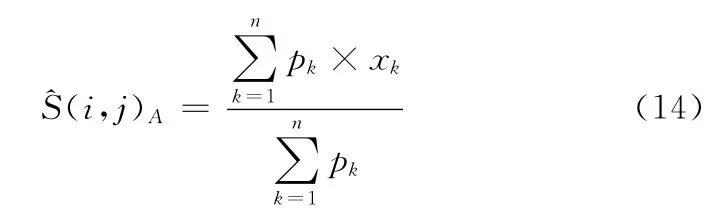
其中,xk∈;n是中的元素个数;pK是权值,其值由高斯式(15)确定
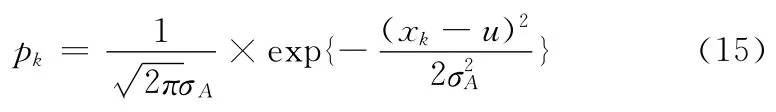
其中,u=MF(i,j),xk∈。即越接近u的xk权值越大;离u越远,权值越小。
其次是表征局部轮廓信息的灰度值重构。采用最具有相似性的灰度值(如图3(c)白色线条所对应的灰度值),而不是窗口中所有的灰度值来重构。由于灰度值之间的相似性,可以用离散程度来表示,离散程度越小,说明数据越相似。而数据之间的离散程度,可以用标准差来衡量。即,标准差越小,说明数据越相似。当在3x3窗口内考虑相似性时,由于数据量少,易受噪声的干扰,所以此处选择5x5的窗口,如图4所示。

表2 NeighShrink_Sure去噪运算时间

图4 5x5窗口灰度值
轮廓在较小的范围内可以用线段近似,考虑图4中4条直线上的灰度值集合:
水平直线上元素集合l1:{x3,x8,x13,x18,x23};
垂直直线上元素集合l2:{x11,x12,x13,x14,x15};
45度(225度)直线上元素集合l3:{x5,x9,x13,x17,x21};
135度(315度)直线上元素集合l4:{x1,x7,x13,x19,x25}。
这4个集合的均值和标准差分别是μli,σli,i=1,2,3,4。σl=min{σl1i,σl2i,σl3i,σl4i},则σl对应的集合li的均值μli即为第二个重构要素^S(i,j)L。
然后,点信息^S(i,j)P用式(16)计算
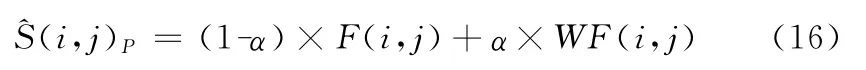
其中,α的值为式(13)计算的结果。式(16)表明,如果噪声较弱,则点信息趋向于用污染图像中的灰度值来表示;如果噪声较强,则趋于用维纳滤波后的值来表示。
最后,边缘区域中的灰度值用分别代表了局部、轮廓和点信息的3个值合成,即
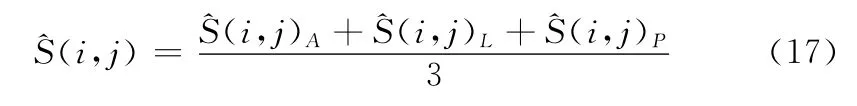
3 本文算法步骤
综上所述,本文分区域去噪算法如下:
步骤1 按式(6)计算估计噪声^N;
步骤2 按式(10)计算用于加速的矩阵F2,N 2;
步骤3 按式(11)计算局部标准差,并按式(7)得到T值;根据T与1.5的关系把图像进行划分;
步骤4 平滑区域的灰度值按式(12)去噪;边缘区域的灰度值按式(17)去噪,得到最终合成估计图像^S。
4 实验仿真与分析
选择大小为512×512像素、灰度级为256的Lena图像做为测试样本,其视觉效果如图5所示。

图5 σ=20时,不同算法的去噪效果
相关的峰值信噪比(PSNR)和本文算法处理的时间见表3。
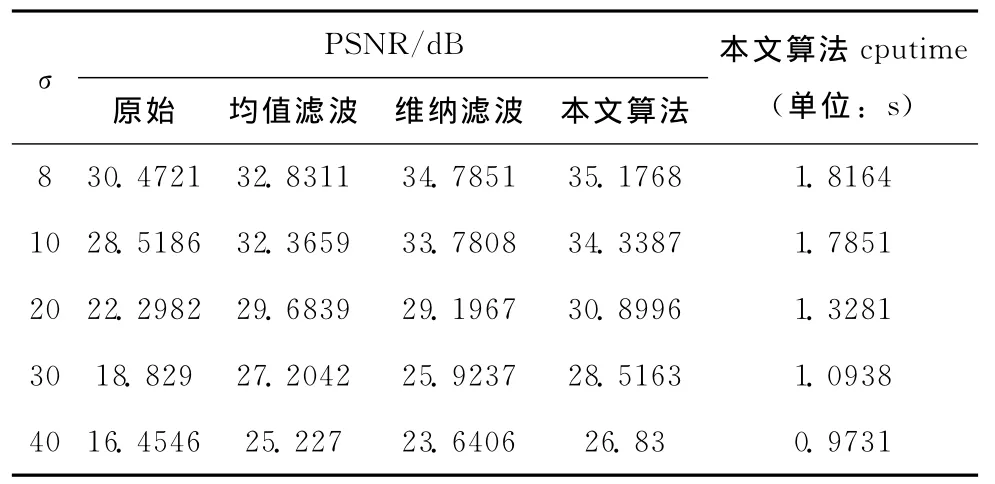
表3 Lena去噪后PSNR及处理时间
从表3中可以看到,σ=8、10、20、30和40时,按本文算法去噪后图像的PSNR要比原来的PSNR分别提高了4.7047dB、5.8201dB、8.6014dB、9.6873dB和10.3754dB。另外可以看到本文算法整个去噪过程花费的时间也较小,具有较高的效时比。
为了进一步验证本文方法的有效性,再对大小为384×512像素小的Peppers图像进行去噪。同样取得较高的峰值信噪比和较高的运行速度。相关的PSNR和处理时间见表4。
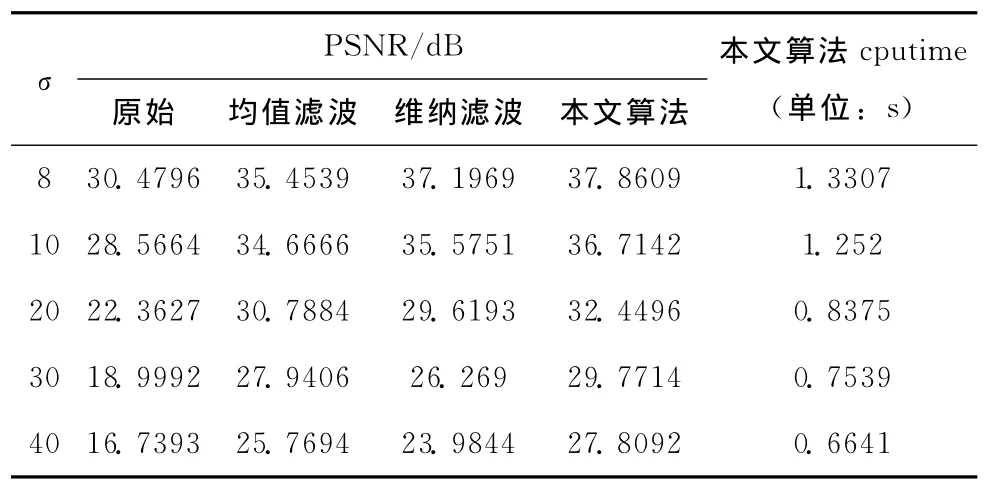
表4 Peppers去噪后PSNR及处理时间
把表3、表4和表2进行对比可以发现,本文去噪算法整体上有较快的运算速度,同时处理后的图像依然有较高的峰值信噪比。从图5中也可以看到,本文算法处理后的图像能够较好地保留图像边缘等细节信息。
5 结束语
本文提出了一种快速分区域去噪算法,获得了较好的处理效果和较快的运行速度。该算法创新之处在于:首先,与以往分区域算法相比,该算法划分区域时不需要人为地选择阈值参数,避免了结果的不确定性。其次,创新地用式(10)引进了两个和待处理图像一样小的矩阵用于方差计算,用较小的内存开销却获得了处理速度的成本提高,解决了许多程序中用方差处理问题时运行速度过慢的问题,提升了算法的实用价值。
实验结果表明,用本文算法处理后的图像有较高的峰值信噪比,而且还能较好地保留图像轮廓等细节信息。重要的是,该算法在达到同类算法类似效果的同时,具有较快的运算速度。下一步将对算法改进,使其适用于具有复杂纹理结构的图像。
[1]CHEN Wen,FANG Xiangzhong.Approximate shape parameter estimation of generalized Gaussian noise in image[J].Computer Engineering,2011,37(22):204-206(in Chinese).[陈文,方向忠.图像中广义高斯噪声形状参数的近似估计[J].计算机工程,2011,37(22):204-206.]
[2]XIN Guojiang,ZOU Beiji,LI Jianfeng,et al.Image segmentation with PCNN model and maximum of variance ratio[J].Journal of Image and Graphics,2011,16(7):1310-1316(in Chinese)[辛国江,邹北骥,李建锋,等.结合最大方差比准则和PCNN模型的图像分割[J].中国图象图形学报,2011,16(7):1310-1316.]
[3]WU Haiyang,WANG Hui,PEI Baoquan.Improved threshhold for image denoising based on neighshrink[J].Computer Engineering and Applications,2011,47(27):203-220(in Chinese)[武海洋,王慧,裴宝全.一种阈值改进的邻域小波系数法图像去噪[J].计算机工程与应用,2011,47(27):203-220.]
[4]GONG Xiaolin,MAO Ruiquan.An image denoising algorithm based on PCNN and local Wiener filter[J].Journal of Beijing University of Posts and Telecommunications,2011,34(5):67-70(in Chinese).[宫宵霖,毛瑞全.结合PCNN和局部维纳滤波的图像去噪[J].北京邮电大学学报,2011,34(5):67-70.]
[5]Tuan-Anh Ngugen,Won-Seon Song,Min-Cheol Hong.Spatially adaptive denoising algorithm for a single image corrupted by Gaussian noise[J].IEEE Transaction on Consumer Electronics,2010,56(3):1610-1614.
[6]JIANG Chunmiao,ZHOU Zuofeng.Efficient method for removing mixed noise in images[J].Computer Engineering and Applications,2009,45(24):183-185(in Chinese).[姜春苗,周祚峰.去除图像中高斯脉冲噪声的有效方法[J].计算机工程与应用,2009,45(24):183-185.]
[7]GUO Shuixia,TANG Yongjun.Extension and application of Wiener filtering in image processing[J].Computer Engineering and Applications,2008,44(14):178-180(in Chinese).[郭水霞,唐拥军.图像处理中维纳滤波器的推广与应用[J].计算机工程与运用,2008,44(14):178-180.]
[8]DAI Fang,XUE Jianru,ZHENG Nanning.Embedding intrinsic model function into anisotropic diffusion equation for image denoising[J].Journal of Electronics and Information Technology,2008,30(3):509-513(in Chinese).[戴芳,薛建儒,郑南宁.嵌入固有模态函数的各向异性扩散方程用于图像降噪[J].电子与信息学报,2008,30(3):509-513.]
[9]HONG Juntian,TAO Jianfeng,LI Gang,et al.Noise reduction of digital image based on gray correlation degree[J].Journal of Wuhan University of Technology(Transportation Science and Engineering),2006,30(4):639-641(in Chinese).[洪俊田,陶剑锋,李刚,等.基于灰色关联的数字图像去噪研究[J].武汉理工大学学报(交通科学与工程版),2006,30(4):639-641.]
[10]GONG Qu,AN Yanping,LUO Shufen.Image denoising combined with wavelet transform based on region segmentation[J].Computer Engineering and Applications,2010,46(34):191-194(in Chinese).[龚劬,安艳萍,罗淑芬.一种基于图像区域分割的小波去噪方法[J].计算机工程与应用,2010,46(34):191-194.]
[11]SUN X Z,Anastasios N Venetsanopulos.Adaptive schemes for noise filtering and edge detection by use of local statistics[J].IEEE Transactions on Circuits and Systems,1998,35(1):57-69.
[12]Rafael C Gonzalez,Richard E Woods.Digital image processing[M].3rd ed.Beijing:Publishing House of Electronics Industry,2011:714-748.
[13]Lee J S.Refined filtering of image noise using local statistics[J].Computer Graphics and Image Processing,1981,15(4):380-389.

