改进的软硬阈值法及其在地震数据降噪中的研究

刘 剑，秦飞龙，成亚丽

(成都工业学院 a.汽车与交通学院；b.大数据与人工智能学院，成都 611730)

1 新阈值降噪算法

1.1 算法基础

对于一组观测信号：

f(t)=s(t)+n(t)，

(1)

式中：f(t)是含有噪声的观测信号，s(t)是有效信号，n(t)是随机干扰信号。

如果有N个采样点，对观察信号f(t)的一维小波变化[11]如下：

(2)

式中：Wj,k为小波系数，ψ(t)为一个母小波。一维离散小波重构变换、二维小波分解和重构变换见文献[1]。对分解的小波系数利用软、硬阈值函数进行去噪。

软、硬阈值降噪原理为[12]：

(3)

(4)

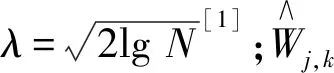
经过软阈值降噪处理后的小波系数整体上具有连续性，然而对大于阈值的信号进行恒定方式压缩，会去除一些高频信号，因此经过小波重构的信号不能代表真实信息。硬阈值降噪能够避免软阈值降噪恒定偏差的影响，但是处理后的小波系数在阈值处不具有连续性，很有可能给重构数据带来振荡影响，使原信息光滑度变差。因此在软、硬阈值降噪原理基础上提出了一种改进的新阈值降噪算法，以弥补软、硬阈值降噪的缺陷。

1.2 新阈值降噪算法

在软、硬阈值基础上设计的新的阈值降噪函数如下：

(5)

式中：ν=β-(|Wj,k|-λ)2，0≤β≤1。根据新阈值函数表达式可以得出以下结论：

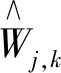
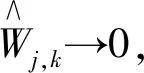
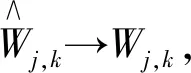
可见，新阈值降噪函数同时具备软、硬阈值函数降噪功能。其优点是不仅避免了软阈值函数在恒定偏差上的影响，还克服了硬阈值函数在阈值处的不连续性影响。因此新阈值降噪更具有优势。

2 仿真实验

为了确定新阈值降噪算法的有效性，选取采样间隔1 ms，采样点为1 000的有效信号s(图1(a))，给s添加随机噪声获得观测信号o(图1(b))，选取三层小波分解[2,13]，利用软、硬阈值函数，新阈值函数分别对观测信号进行噪声压制，再通过小波重构信号得到降噪后的有效信号(图2)。由图2知，经过新阈值降噪，信号的峰值毛刺干扰被消除，几乎无信号损失和失真，对噪声进行了有效消除，降噪效果优于软、硬阈值降噪。

图1 原始信号Fig.1 The original signal

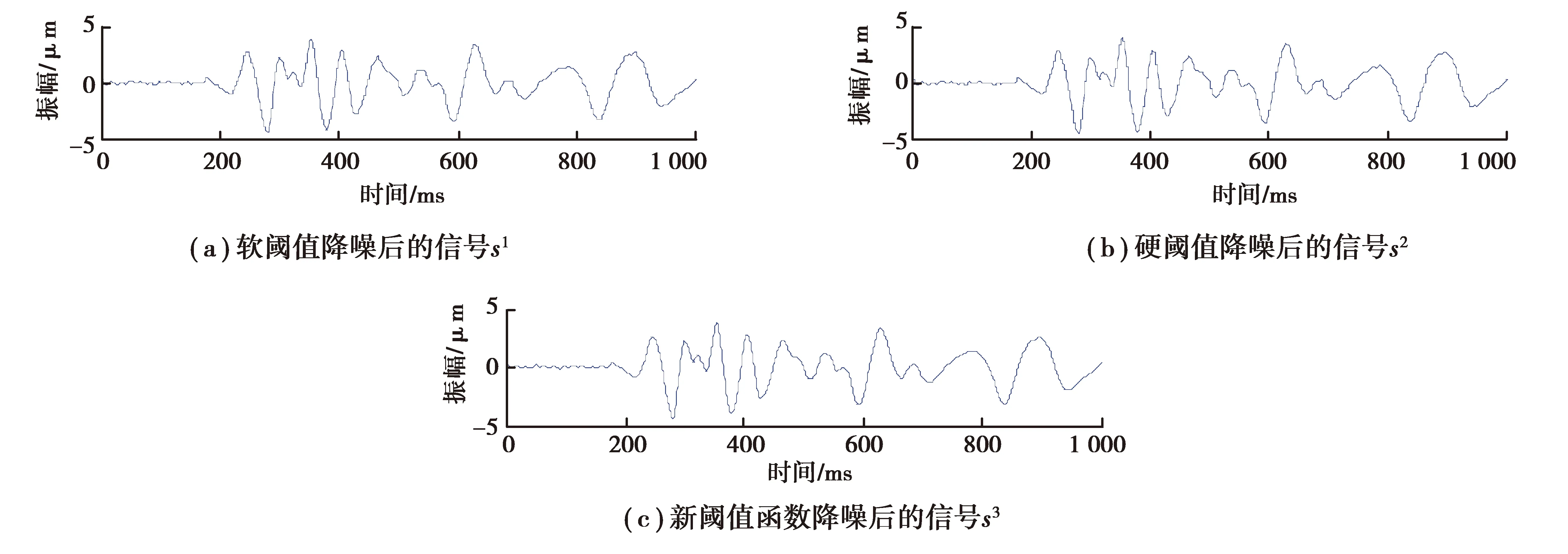
图2 降噪处理Fig.2 The data denoising

用信噪比(SNR)和均方根误差(RMSE)对软、硬阈值函数和新阈值函数的降噪效果进行评价[14]。

(6)

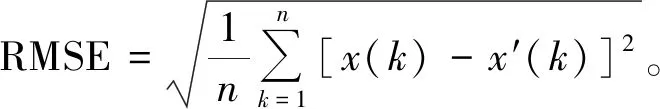
(7)

式中：x(k)为原始观测信号；x′(k)为降噪后的信号；SNR值越大，降噪效果越好；RMSE值越小，降噪效果越好。

经计算，软、硬阈值函数和新阈值函数降噪后的SNR和RMSE如表1所示。由表1知，新阈值降噪的SNR最大，RMSE最小，从而进一步说明新阈值降噪较软、硬阈值函数降噪更合理。目前在小波变换中常用的小波基有symN系列、dbN系列等，而地震数据降噪常选取symN系列[15]。因此选取不同的symN，利用式(6)和(7)，得出不同symN下新阈值函数降噪后的信号SNR和RMSE(图3)。由图3知，sym 3的SNR最大，RMSE最小。因此新阈值函数选取sym 3，降噪效果最佳。

3 实际地震数据降噪处理

将提出的新阈值函数用于实际地震数据降噪处理，数据来自中国地质调查局计划项目(1212010916040)，数据样本采样间隔道号为1，采样点数为6 000，采样间隔为1 ms。为了便于显示，截取其中的1～111道地震信号数据进行降噪处理(图4(a))。由图4(a)知，原始地震数据剖面被随机噪声干扰严重，分辨率低，看不出地震数据形态，不利后期地质解释。因此，选取小波基为sym 3，3层小波分解。利用小波变换中的软、硬阈值函数对原始地震数据进行降噪，降噪后的信号分别如图4(b)(c)所示。由图4(b)(c)知，软、硬阈值函数能够去除地震数据大部分干扰噪声，地震分辨率有所改善，然而降噪效果不理想，仍然存在大量噪声影响地震剖面，分辨不高。利用所提出的新阈值函数对原始地震数据进行降噪处理，降噪后的信号结果如图4(d)所示。由图4(d)知，整个降噪后的地震剖面数据双曲线特征明显，纹理清晰，分辨率高，几乎所有干扰噪声均被移除，表明新阈值函数降噪效果比软、硬阈值函数降噪效果更理想。

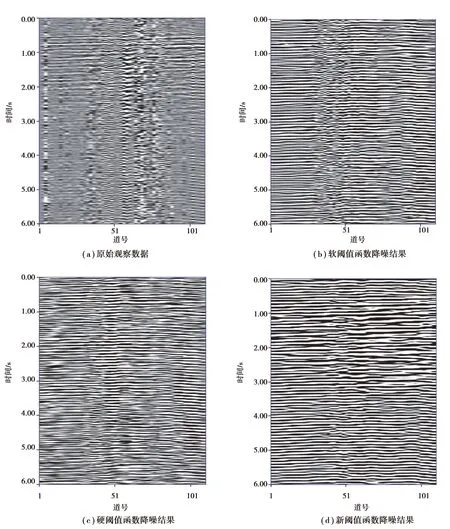
图4 地震数据降噪Fig.4 The seismic data denoising

4 结 论

在软、硬阈值函数降噪基础上提出了一种新阈值降噪函数，结论如下：

1)新的阈值降噪函数同时具备软、硬阈值降噪函数功能，其优点是避免了软阈值函数在恒定偏差上的影响，也避免了硬阈值函数在阈值处的不连续性影响；

2)通过仿真实验确定了新阈值函数的小波基为sym 3，信噪比(SNR)和均方根误差(RMSE)结果表明新阈值函数降噪效果更好；

3)在实际数据降噪处理中，新阈值函数能够去除地震数据的各类干扰噪声，降噪后的地震剖面分辨率高，对比软、硬阈值函数结果表明新阈值函数降噪更有效。