高中数学教学中运用合情推理模式的初探

黄金晶

【摘要】在新课程改革大力推进的背景下，培养学生核心素养已经成为各学科教学的主要任务.而在高中数学教学中，逻辑推理能力是一种重要的数学素质，也是培养学生核心素养的关键和重点.本文中，笔者对合情推理模式在高中数学教学中的运用做出相关介绍，希望通过该模式的运用，可以推动学生创新发展，为学生的数学核心素养培养落实提供保障.

【关键词】高中数学;合情推理;模式运用

前 言

合情推理是一种思维形式，也是现代数学教育培养的核心素质内容之一.在高中数学教学中，教师可以通过合情推理模式培养学生的思维素质，即让学生利用已有的知识和经验，将自身置于某种情境或认知过程当中，引导学生通过观察、归纳、猜想、类比的方式，自主尝试获得知识问题的结论.在新课程背景下，对合情推理模式的运用做出探索研究具有非常重要的意义.

1 高中数学教学中运用合情推理模式的意义

合情推理模式在高中数学教学中的运用具有重要意义.首先，从学科性质分析，数学既是一门系统的演绎科学，也是一门实验性的归纳科学.在传统的高中数学教学中，教师多将注意力集中于严谨论证，将培养学生严谨推理能力作为教学重点，但忽视了对学生合情推理能力的培养.事实上，在学生数学学习过程中，合情推理扮演着重要的角色.因为数学思维是一种发展创造性思维，想象、感悟、联想、直觉、类比才是数学学习发展的动力源泉，“处于发现过程中的数学”这一学科性质，决定了合情推理模式在高中数学教学中的运用价值.其次，从教育任务角度分析，当下正处于信息经济时代，教育的任务不再是培养单纯的知识型人才，更为重要的是实现智能型人才的培养，因此灌输式、填鸭式的教学模式已经与当下的教育时代任务不符，只有引导学生自主去发现问题、探究问题，体验数学知识的发展过程，才能够实现培养智能型人才的目的[1].而合情推理教学模式的运用，充分发挥了学生的主体作用，让学生自身经历推理、检测、修正的过程，自主发现通往真理的道路，因此合情推理教学是当下现代人才教育的必然趋势和需求.最后，从高考考查趋势分析，通过对近几年的高考试题对比可以发现，归纳、类比成为近些年高考的重点，而这正是合情推理中常用的科学方法.因此，为促使学生能够在高考中取得佳绩，在高中数学教学中运用合理推理教学模式也是十分重要的.

2 高中数学教学中运用合情推理模式的方法

2.1 在数学概念教学中的运用

数学概念教学是高中数学教学中最为基本的内容.对于学生而言，只有将数学基础概念牢牢掌握，并深深嵌入原有的认知结构之中，实现新旧知识的同化理解，这样才能为学生的数学学习打下坚实的基础.而合情推理模式在高中数学概念教学中的应用，不再是将现成的教学理论强加给学生，而是从学生的认知结构出发，通过设计学生乐于接受的合情推理情境，与学生共同以发现者的姿态，共同参与到对数学概念的研究探索当中，从而帮助学生认识数学知识概念的本质.具体而言，数学概念的形成过程包括八个心理阶段，分别是辨别（各种研究事物）、分化（对研究事物的属性进行分化）、类化（分化出不同事物的属性，找出其中共同的属性）、抽象（能够对事物的本质属性做出假设）、检验（能够在特定的情境之中对假定的属性做出验证）、概括（找出其中的关键属性，并用自身的话语进行定义表示）、强化（可以将自己获得的概念推广到其他事物的理解之中，实现概念的外延）、形式化（将自身理解的概念与对应的数学公式符号进行替换表示）.[2]由此可以看出，学生对数学知识概念的认知理解是一个从特殊到一般再到特殊的过程.在运用合情推理模式的概念教学中，教师应该从学生数学知识概念形成的八个心理阶段出发，带领学生合理推理，获得知识概念.

下面，笔者将以“棱柱概念”教学为例，阐述如何在数学概念教学中运用合情推理模式.

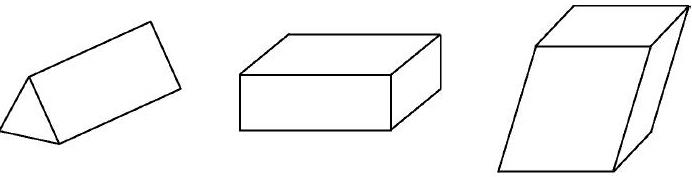
（1）辨别.教师可以向学生展示棱柱形体图片，并向学生提出这样的问题“棱柱的大致形态如何？能否列举出生活之中见到的一些棱柱几何体物品”，让学生大胆地进行联想和猜测，对研究事物形成基本的认识.

（2）分化.教師可以继续向学生提出“展示的棱柱几何体分别有哪些特征性质”，引导学生对展示图片进行深入的观察，总结出可以发现的大致特征性质，如边的特征、角的特征等，以此让学生对棱柱的具体特征属性做出分化，并促使学生的观察、分析能力得到培养.

（3）类化.教师可以向学生提出这样的问题：“上述棱柱几何体有哪些共同的性质？”学生就会发现，三个棱柱体虽然形体上有所差异，但都具有两个边相互平行、各个面均是平行四边形且相邻的两个面的交线平行且相等.

（4）抽象、检验、概况.让学生在上述研究认识的基础上，自觉尝试对棱柱的概念做出抽象概况，并尝试对概念做出验证，如列举反例等，以此培养学生从特殊到一般的归纳概况能力.

（5）强化与形式化.教师可以进一步向学生展示这样的一个几何体，并向学生提问：“该几何体是棱柱吗？为什么？能否用棱柱的符号去表示该几何体的底面、侧面、侧楞和定点？”[3]

在这样的问题中，引导学生从一般到特殊，相信在这样的合情推理模式运用下，学生对棱柱知识概念一定会形成全面且深入的认识.

2.2 在数学解题教学中的运用

著名数学家波利亚曾经说过：“数学要在解题中合情推理，学会猜想.”由此可以看出，合情推理是学习数学的一种重要方式.合情推理的思维方法可以为数学猜想提供依据，这可以让学生从解题的困境和瓶颈之中解脱出来，因此在高中数学教学中，教师在解题教学之中运用合情推理模式是具有一定适用性的，可以更好地助力学生解题能力的提升.具体而言，在运用合情推理模式的解题教学中，教师一定要认识到解题是对数学方法的探索，是需求已知向未知的转换.一般情况下，学生解题的思维程序大体可以分为三个步骤，即回想、联想和猜想.具体运用合情推理的解题应有以下几个方面的侧重：

第一，重视对基础知识的系统梳理和运用.教师要认识到绝大部分的数学考题，考查的都是学生知识结构的系统性，学生只有基础知识结构完善，才能理解题的本质，这样才能迅速地寻找解题思路.因此，在运用合情推理模式的解題教学中，教师在学生解题的过程中可以引导学生认真分析问题，立足于已知条件，将与问题有关的概念、定理采用列图表或者列图示的方式表示出来，以此形成对解答问题的完整知识结构，获得寻找解题思路的必要条件.

第二，重视对重要知识的加深理解.提高加工水平，关注问题细节，并对知识进行多方面的感知和联想，可使认知结构更加完善.在运用合情推理模式进行解题教学时，教师能够带领学生对重要知识进行深入加工是十分必要的环节.[4]以函数性质相关问题解题为例，函数单调性是本章知识的重点，多数与函数性质有关的问题，都是通过单调性或者单调性图像进行求解的.因此，在合情推理模式运用的教学中，建议教师可以在函数这一章的大系统复习中，单独开辟出一个关于单调性的小系统解题联系，并以题组的形式带领学生对知识点进行深加工，让学生从具体问题抽象出知识点的连接，让学生一边做题，一边串联重要知识点，从而不断地丰富学生的解题联想，促使学生的解题思路和解题思维得到不断拓宽.

第三，注重数学思想方法的形成.著名的教育学家布鲁纳曾经说过：“无论是哪一学科教学，都要注重学生思想方面的形成掌握.”在高中数学教学中更是如此.学生只有掌握数学解题的思想和方法，其解题能力才能真正得到提升.因此，在运用合情推理模式进行解题教学时，教师还应该在解题训练的过程中，有意识地将归纳推理、类比推理等数学思想方面传授给学生，让学生体会数学思想在解题中的巨大作用，从而带动学生解题能力不断攀升.

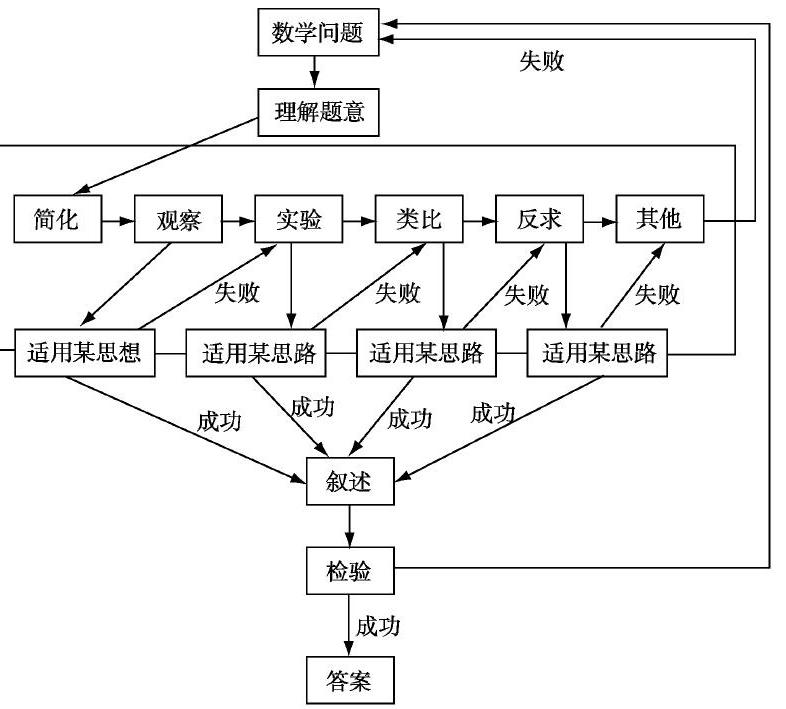
本次研究中，我们对运用合情推理模式的高中数学解题思路过程做出了概况，具体如下图所示：

2.3 在研究性学习中的运用

研究性学习是新课标背景下培养学生创新意识和实践能力的重要学习方法.在研究性学习中，教师要结合数学学科内容设置相关的研究课题，在教师的指导下，引导学生共同参与，通过对数学研究课题的深入实践，促使学生的科学知识和科学精神得到不断发展和提升.现在，研究性学习已在各学校如火如荼地展开，常见研究性学习步骤为：问题引出→主动探究→合作交流→解决问题.而在研究性学习中，合情推理模式具有重要的应用价值.具体的应用方法如下：首先，营造宽松良好的猜想氛围.教师不要急于将知识传授给学生，而是应该为学生设置与研究课题内容有关的情景，以此作为学生思维的突破口，让学生在“需要”与“认知结构矛盾”的风口浪尖下，引导学生进入情景之中并深入探究.同时，在研究性学习中运用合情推理模式，要注重知识的发生过程，依照“合情推理+证明”的发现问题和解决问题的科学思维，尊重学生的生活经验和认知基础，理解学生独特的感受和理解，以此实现更好的研究性学习效果.[5]其次，培养学生合情推理能力，教师必须要懂得猜想，在运用合情推理模式的教学研究性学习中，教师应该认识到，若是想要让学生掌握此种方法，教师自身必须要先掌握它.因此，教师在授予学生一定数学知识的同时，教师也应该根据研究性学习问题的特点，并站在更高的高度，结合学生的思维特点，设置最近发展区，这样才能够为学生的研究性学习提供更加充分的保障.

总 结

合情推理模式与高中数学教学是极为契合的.在高中数学教学中，教师可以在概念教学、解题教学、研究性学习中运用合情推理模式，以此为学生提供自主观察、归纳、猜想、类比的空间.在这个过程中，学生将会积累更多的感悟经验，学生的推理思维能力也会得到不断的拓宽，这对学生的数学学习发展是大有裨益的.因此，在今后的高中数学教学中，教师有必要对合情推理模式做出更加深入的探索研究.

【参考文献】

[1]郭昌端.合情推理能力在高中数学课堂教学中的渗透[J].文理导航（中旬），2020（06）：10-12.

[2]严佳云.高中数学教学中运用合情推理模式初探[J].数学教学通讯，2020（12）：15-16.

[3]杨原明.高中数学教学中进行合情推理能力培养的尝试思路构架实践[J].数学教学通讯，2020（03）：38-39.

[4]李新岳.浅析基于逻辑推理能力发展的高中数学核心素养培养[J].新课程（下），2019（11）：192.

[5]陈桂芬.高中数学教学中的推理猜想引导——评《数学与猜想（第二卷）：合情推理模式》[J].中国教育学刊，2019（08）：124.