浅谈数形结合思想在初中数学教学中的渗透

徐亚妮 夏学升

【摘要】新课改背景下，初中数学教师需要对以往传统教学思想加以改变，创新其教学思想及模式，采用最新的教学思想激发学生的学习兴趣，让学生能够在兴趣的影响下形成良好的自学习惯，进而实现数学能力的提升.在教学中合理融入数形结合思想，不仅可以让学生发掘图形与数学知识之间的关系，同时能够建立起正确的解题思路.

【关键词】数形结合;初中数学;教学渗透

引 言

学生数据基础形成的关键期便是初中阶段，在此阶段充分融入数形结合思想，不仅可以培养学生的数学思维，同时能够通过图形对学生思维实现有效扩展，并能让学生以学习兴趣为基础，逐渐强化其对于问题的思考、解决、探索能力.

1 数形结合思想运用于初中数学的价值

初中数学教学内容较为丰富，课本中也存在着非常多的图形.同时，相较于其他科目，其形式上更加具有趣味性，通过图形进行知识点的描述能够让学生更清晰地认识到数学的理论知识.初中数学的学习对发展学生思维具有非常重要的作用，在教学中教师对符合现代化教学理念的教学方式进行探索，可有效提升初中阶段学生的思维水平.如今，数形结合在初中数学中的应用十分重要，因此教师需在教学中强化学生数形结合的能力，让学生能够在短时间内掌握知识点的本质.

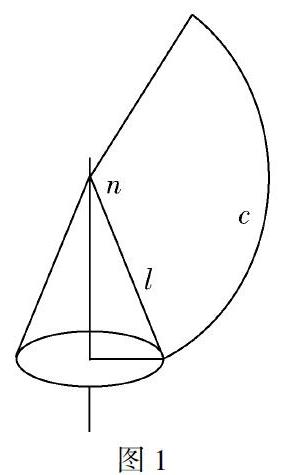
首先，课上教学时，教师需引领学生通过数形结合的方法对知识点进行理解，通过一段时间的学习便可有效提升学生处理问题的能力.其次，在课堂中，教师在进行例题或者难题的讲解时，可以通过图形变换的方式辅助自己的教学，让学生能够在课堂上逐渐掌握数形结合的方法，并对问题进行处理，进而实现对数学图形理解的加深.例如，教师在讲解锥形和扇形间的变换时（如图1所示），教师利用图形可让学生直观地观察到其中所具有的变换关系.待教材中知识讲解完毕后，教师可为学生布置与图形有关的练习，进一步强化学生应用数形结合进行解题的能力.

2 数形结合思想在初中数学中的应用价值

2.1 降低数学理解难度

从初中生的角度来看，数学知识的逻辑性较强，学生在学习时常常会遇到各种难题.尤其在初中数学的实际教育中，往往存在着众多复杂且难以掌握的数学理论及公式，而且其中的很多理论及公式并没有推理过程，这进一步加大了初中生的数学学习难度.受传统教育模式影响，教师的教学模式往往以 “填鸭式”为主，让学生“死记硬背”数学的概念及公式，这样一来势必会阻碍学生学习效率的提升.在数学学科的教学中，合理融入 “数”与 “形”相结合的思想，通过对图像与数字之间的关系进行图形表征，能够潜在地提升学生对于数与形的认识，让其学习效率大幅提升，并实现学习质量的进一步强化.

2.2 增强学生数学思维能力

学生自身的思维能力会对其学习数学的效率产生直接的影响.初中阶段，学生的数学思维已经由原来的直观思维逐渐转变为抽象思维，但是对于初中教师来说，教学中需以数学这门课程中所含有的抽象性不断强化学生们的思维，为提升其学习数学的效率奠定扎实的基础.在此背景之下，教师通过数形结合思想的应用，可以引导学生通过直观的图像表现出复杂的数量关系，从而实现对于学生数学思维的完善以及相应能力的提升.

3 初中数学教学中的问题

3.1 概念性知识居多

在实际的数学理论知识展示过程中，初中教师往往通过多样化的教学模式进行相应内容的授课.然而，从实际的教学大背景来看，不同学生所具有的接受能力都是存在很大差异的，而这种问题的存在会对教师的教学效果产生直接的影响.为了保证学生对于知识能够充分掌握，教师需要将概念性的内容及知识尽可能浅显地表达出来，并强化相应的习题训练，以此巩固课堂教学的内容.而实际上，这样的教学模式无助于学生思想的培养，极易导致学生丧失数学的学习信心.教师在数学教学中利用概念的内容为学生进行知识的讲解，此类情况需得到妥善的处理，而应科学融入数形结合思想，让学生能够掌握适当的学习方法，以此提升其学习效率.

3.2 缺乏综合性

初中数学是一门综合性较强的学科，在教学中，倘若教师只关注知识的灌输，则无法收获最佳的教学效果，只有同实际相联系，方可激起学生的学习热情.但是从目前的教学情况来看，大部分教师还是以课堂教学为主导，在对学生的数学思想进行培养时所采用的教学模式缺少多样性，有思想但未与实践相联系，导致学生无法深入了解数学思想.对此，教师需要合理应用數形结合思想，同时需要提升学生的实践水平，通过实践让学生能够在解题中灵活运用数学思想，保证学生能够全面掌握数学的学习方法及技巧.

4 数形结合思想在初中数学教学中的具体应用

4.1 在方程教学中应用数形结合思想

从教学中出现的问题可以看出，在激发学生学习热情方面教师具有重要作用.数学教师需通过元化的教学方式，赋予教学内容以趣味性、形象性，让学生能够在课堂上参与其中.目前，数形结合的教学思想在教学中具有重要的作用，在数形结合思想的促进下可实现学校教学质量的逐步提升.

数形结合思想主要指的是数学中通过结合“数”“形”的思想，并利用其加深学生对于数学图形与概念之间关系的认知.在教学中则表现为教师将复杂过程简洁化，直观表现出数学问题的含义.例如，在讲解“一元二次方程”的问题时，教师可通过此方法将问题更加直观地表现出来.从ax2+bx+c=0的问题来看，通过数形结合思想的使用，可对其多重性质实现准确的认识.当a>0时，可画出开口朝上的函数图像，并与0和b2-4ac之间具有的关系相结合，可判断此方程是否与x轴有相交点.此外，在实际教学过程中，教师需正确引领学生合理运用数形结合方法展开解题工作.在计算过程中多次结合数字与图像，在无形中对学生的数学学习产生影响，潜移默化地促进学生养成通过数形结合方式进行问题处理的能力.

4.2 在代数中采用数形结合思想

在教学中，概念方面的教学是基础.而数学的概念性知识是经历了多次精简以及概括而逐步形成的，所以与其他文字内容相比较，数学概念非常晦涩且难以理解.在数学知识当中，也有很多知识概念太过抽象、复杂，学生理解难度极大.在此情况下，教师可积极使用数形结合的教学方法展开说明，通过几何图形表达出知识文字当中的内容，协助学生对知识进行学习.在实际教学中，教师需自然而然地将数形结合思想融入學生的思维当中，潜移默化地对学生产生影响，采用由浅入深、从简到繁的方式，对学生的自学热情实现有效激发，让学生在学习数学的过程中能够体会到趣味性，进而实现初中数学教学水平的进一步提升.

在初中数学课程中，代数是主要教学内容之一.在常见的代数问题中，常常存在很多的未知数，而画图解题缺乏严谨性，使得学生极易出现计算方面的错误.而在这时，教师应用数形结合的教学思想，引领学生按照题目的含义进行方程的求解，描绘出现相应的函数图形，进而进行问题的解答.比如题目为：“在y=-x2+2x的函数中，倘若在-1

4.3 在空间与图形中应用数形结合思想

数形结合本质上就是通过几何图形实现数学关系的表达，或通过数学关系进行图形的展示，从而巧妙地结合数字与图形，表现出“1+1>2”的教学效果.在初中的数学课程教学中，融入数形结合思想能够实现知识的形象化，帮助学生掌握课上的教学内容，强化学生的知识记忆.在知识点中融入几何图形，可以让数学关系变得清晰、明了，也可以将抽象的知识内容转变为具体的图像，帮助学生合理解决实际学习中所出现的难题.

教师在使用数形结合的教学思想时，可从生活的点滴之中对教学素材进行挖掘及丰富，对日常生活中所能够运用的事物加以利用，促进学生积极开展实践活动，使他们能主动掌握几何图形空间转换的技巧.例如，在转换几何图形时，教师可通过引导学生对平面图形进行转换.在拆剪盒子的过程中，教师需在课前进行相应教材的准备，与学生一道分析拆剪盒子过程中所发生的空间变化.另外，对于图形的图像转化，可先变为函数关系进而实现数字计算.例如， “y=-x2+4x+5与x轴上A、C两点相交，并与Y轴相较于B点，直线BC之上的曲线是否有一点P，与BC相连所形成的△PBC具有最大的面积？如果存在，求P坐标;如果不存在，请加以说明.”教师可先将函数的线段图像表现出来，随后依照题目要求对各交点进行标记.作与y轴平行线线段将三角形分割为两个三角形，通过两个三角形的面积表示出原三角形面积（如图2所示）.

结束语

通过以上分析我们可以看出，在实际的初中数学教学工作中，教师应用数形结合教育思想，不仅可以保证数学课堂质量的有效提升，同时可以帮助学生对所学知识进行有效掌握，形成良好的思维模式，确保数学学习效率的稳步增强.但在此过程中，教师需坚持“以生为本”的理念，依据实际，合理设计数形结合的应用深度，选用与学生认知能力相适应的教学内容，从而保障学生的数学综合素养能够得到有效发展.

【参考文献】

[1]黄美芬.数形结合并蒂花开：数形结合思想在初中数学教学中的运用[J].科学咨询：教育科研，2020（5）：242-243.

[2]郜金秀.数形结合思想在初中数学教学中的渗透初探[J].数学学习与研究，2020（3）：36.

[3]童琛菲.数形结合思想在初中数学解题教学中的渗透策略[J].数学学习与研究，2020（3）：114.

[4]吴必胜.浅析数形结合思想在初中数学教学中的应用[J].数学学习与研究，2020（2）：56.