立体几何中最短距离的求解策略

马亚斌

立体几何中除证点线面的位置关系，还有较常见的就是角的度量问题，而求线段的长度是平面几何中必须要掌握的内容，但现在立体几何中出现频率比较高的题目是有几个动点和定点，求线段和的最小值.学生想当然地会建立坐标系，转化为求两点间距离来处理，“理想很丰满，现实很残酷”，求f（x）+g（x）的最小值难度更大，绝大部分是行不通的.因为命题人的用意不是考查学生是否会用坐标法，而是要求学生能对立体图形翻转折叠展开在脑海中有清晰的脉络，运用自如，其实对图形的空间想象力要求更高了.综观这类题在高考中或各级各类模拟考试中，对考生都是高难度的挑战.笔者谈点粗浅的解题方法，供读者参考.

一、展平图形用勾股定理

例1 （2018·全国卷Ⅰ）某圆柱的高为2，底

面周长为16，其三视图如图1所示，圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（  ）.

A.217 B.25 C.3  D.2图1

解析 此题首先要解决的问题是知道直观图是什么，M、N的正确位置.由三视图可知，该几何体为如图2（a）所示的圆柱，该圆柱的高为2，底面周长为16.画出该圆柱的侧面展开图，如图2（b）所示，连接MN，则MS=2，SN=4，则从M到N的路径中，最短路径的长度为MS2+SN2=22+42=25.

图2

例2 正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为2，侧棱长为1，则动点从A沿表面移动到D1时的最短路程为.

解析 动点从A沿表面移动到D1的路径有无数条，最短路径只有一条，关键是侧面展开图有不同视角和方式，决定路程长短不一，具体有如下3种情况，可能有最短路径：

①从直观图中直接看出，从A到A1再到D1的路程为1+32;

②如图3所示，从A沿侧面到D1的路程为AD1=AD2+DD21=

（32）2+1=19;

图3           图4

③如图4所示，BD1=1+6，AB=2，所以AD1=BD21+AB2=9+26;

显然9+26<1+32<19，故动点从A沿表面移动到D1时的最短路程为9+26.

（例2升级版）如图5所示，在棱长为1的正方体ABCD-A1B1C1D1中，P，Q分别为BD1，BB1上的动点，则△C1PQ周长的最小值为（  ）.

A.2153      B.4+22

C.4+832D.2133

图5           图6

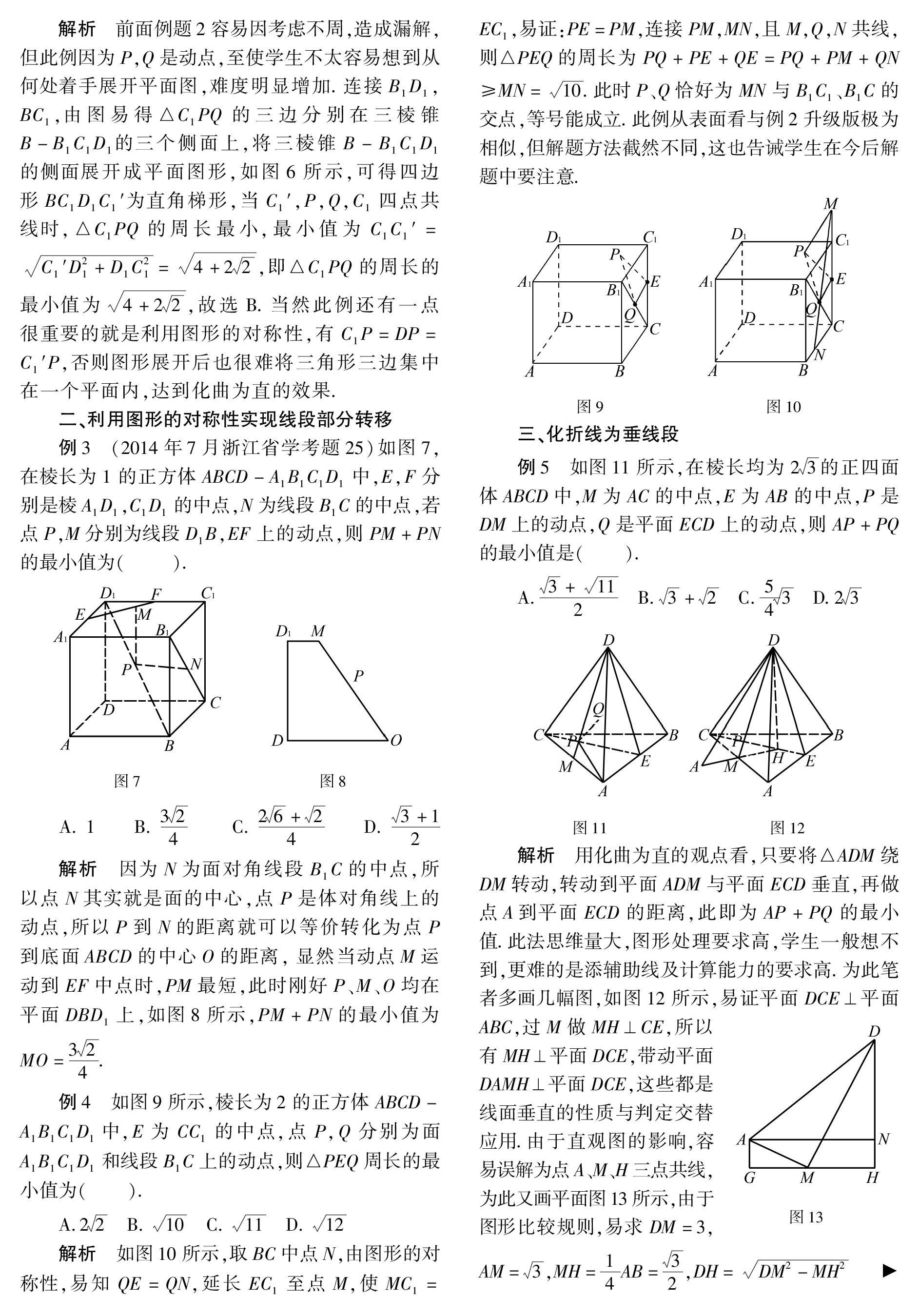
解析 前面例题2容易因考虑不周，造成漏解，但此例因为P，Q是动点，至使学生不太容易想到从何处着手展开平面图，难度明显增加.连接B1D1，BC1，由图易得△C1PQ的三边分别在三棱锥

B-B1C1D1的三个侧面上，将三棱锥B-B1C1D1的侧面展开成平面图形，如图6所示，可得四边形BC1D1C1′为直角梯形，当C1′，P，Q，C1四点共线时，△C1PQ的周长最小，最小值为C1C1′=C1′D21+D1C21=4+22，即△C1PQ的周长的最小值为

4+22，故选B.当然此例还有一点很重要的就是利用图形的对称性，有C1P=DP=C1′P，否则图形展开后也很难将三角形三边集中在一个平面内，达到化曲为直的效果.

二、利用图形的对称性实现线段部分转移

例3 （2014年7月浙江省学考题25）如图7，在棱长为1的正方体ABCD-A1B1C1D1中，E，F分别是棱A1D1，C1D1的中点，N为线段B1C的中点，若点P，M分别为线段D1B，EF上的动点，则PM+PN的最小值为（    ）.

图7           圖8

A. 1  B. 324   C. 26+24  D. 3+12解析 因为N为面对角线段B1C的中点，所以点N其实就是面的中心，点P是体对角线上的动点，所以P到N的距离就可以等价转化为点P到底面ABCD的中心O的距离， 显然当动点M运动到EF中点时，PM最短，此时刚好P、M、O均在平面DBD1上，如图8所示，PM+PN的最小值为MO=324.

例4 如图9所示，棱长为2的正方体ABCD-A1B1C1D1中，E为CC1的中点，点P，Q分别为面A1B1C1D1和线段B1C上的动点，则△PEQ周长的最小值为（  ）.

A.22 B.10 C.11 D.12

解析 如图10所示，取BC中点N，由图形的对称性，易知QE=QN，延长EC1至点M，使MC1=EC1，易证：PE=PM，连接PM，MN，且M，Q，N共线，则△PEQ的周长为PQ+PE+QE=PQ+PM+QN≥MN=10.此时P、Q恰好为MN与B1C1、B1C的交点，等号能成立.此例从表面看与例2升级版极为相似，但解题方法截然不同，这也告诫学生在今后解题中要注意.图9          图10

三、化折线为垂线段

例5 如图11所示，在棱长均为23的正四面体ABCD中，M为AC的中点，E为AB的中点，P是DM上的动点，Q是平面ECD上的动点，则AP+PQ的最小值是（  ）.

A.3+112 B.3+2 C.543 D.23圖11          图12

解析 用化曲为直的观点看，只要将△ADM绕DM转动，转动到平面ADM与平面ECD垂直，再做点A到平面ECD的距离，此即为AP+PQ的最小值.此法思维量大，图形处理要求高，学生一般想不到，更难的是添辅助线及计算能力的要求高.为此笔者多画几幅图，如图12所示，易证平面DCE⊥平面ABC，过M做MH⊥CE，所以有MH⊥平面DCE图13，带动平面DAMH⊥平面DCE，这些都是线面垂直的性质与判定交替应用.由于直观图的影响，容易误解为点A、M、H三点共线，为此又画平面图13所示，由于图形比较规则，易求

DM=3，AM=3，MH=14AB=32，DH=DM2-MH2

=332，

又易知∠AMG=∠MDH，

所以GM=AMcos∠AMG=AMcos∠MDH=3×336=112，

所以AP+PQ的最小值等于AN=GM+MH=

3+112.

四、运用解析几何的方法辅助处理

图14

例6 如图14所示，在棱长为2的正四面体S-ABC中，动点P在侧面SAB上，PQ⊥底面ABC，垂足为Q，若PS=32

4PQ，则PC长度的最小值为.

解析 做PH⊥AB于点H，连接QH，则∠PHQ为二面角S-AB-C的平面角，设AB的中点为G，S在平面ABC内的射影为O′（O′为△ABC的中心），连接SG，GO′，SO′，则∠SGO′也是二面角S-AB-C的平面角，则sin∠PHQ=PQPH=

sin∠SGO′=SO′SG=223，所以PH=32

4PQ，所以PH=PS，所以点P的轨迹是侧面SAB内以AB为准线，以S为焦点的抛物线，SH的中点O是抛物线的顶点，O到C的距离就是PC的最小值，

在△SHC中，由余弦定理，得cos∠SHC=

（3）2+（3）2-222×3×3=13，在△PHC中，由余弦定理可知，PC2=（32）2+（3）2-2×32×3×13=114，所以PCmin=

112.

（收稿日期：2021-09-22）