三角函数在翻折型立体几何小题中的应用

焦随心

在立体几何中，引入坐标法能方便解决图形静态时的度量问题，如空间三类角、线段长度、体积等，但还有一些难度较大的翻折动态型题中，要求某个量的范围或最值，对空间想象力缺乏的学生，不引进变量是很难解决的. 锐角三角函数是解三角形的工具，而任意角的三角函数却不限于此，它是一个周期函数，是研究现实世界中周期变化现象的“最有表现力的函数”，生活中最常见的运动模型就有圆周运动，而翻折图形正是圆周运动的一个“片断”，所以用圆心角表示某些变量恰到好处，所求问题就转化为三角函数问题. 笔者呈现几个教学中用过的典型例题，以飨读者.

例1 如图1所示，在菱形ABCD中，∠BAD=60°，线段AD，BD的中点分别为E，F.现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是（  ）.图1

A. （π6，π3）图2

B. （π6，π2]

C. （π3，π2]

D. （π3，2π3）

解析 如图2所示，以F为原点，直线FB，FC分别为x轴，y轴，建立空间直角坐标系，设二面角A-BD-C的大小为θ，取菱形边长为2，则D（-1，0，0），C（0，3，0），A（0，3cosθ，3sinθ），B（1，0，0），所以

E（-12，32cosθ，32sinθ），BE=（-32，32cosθ，

32sinθ），FC=（0，3，0），所以cos=32cosθ94+34.3=12cosθ，因为θ∈0，π，所以

cos∈-12，12，向量BE，FC的夹角范围是π3，2π3，从而异面直线BE与CF所成角的取

值范围是（π3，π2].

例2 如图3所示，已知平面四边形ABCD，AB=BC=3，CD=1，AD=5，∠ADC=90°.沿

直线AC将△ACD翻折成△ACD′，直线AC与BD′所成角的余弦的最大值是.

解析 先找好有利地形，建立空间直角坐标系，设O是AC中点，由已知得AC=6，如图4所示，以OB为x轴，OA为y轴，过O与平面ABC垂直的直线为z轴，建立空间直角坐标系，由题设易求A（0，62，0），B（302，0，0），C（0，-62，0），做DH垂直AC于H，翻折过程中，D′H始终与AC垂直，由射影定理得，CH=CD2CA=66，则OH=63，DH=306.设∠DHD′=α，则D′（-306cosα，-63，306sinα），所以BD′=（-306cosα-302，-63，306sinα），又与AC共线的向量为n=（0，1，0），设直线AC与BD'所成角为θ，所以cosθ=|cos|=639+5cosα，从而当cosα=-1时，cosθ的最大值为66.

例3 如图5所示，平面PAB⊥平面α，ABα，且△PAB为正三角形，点D是平面α内的动点，ABCD是菱形，点O为AB中点，AC与OD交于点Q，lα，且l⊥AB，则PQ与l所成角的正切值的最小值为（  ）.

A.-3+372 B.3+372 C.7 D.3

解析 因为点D是平面α内的动点，ABCD是菱形，故点D是以A为圆心， AB为半径做圆周运动，可令∠BAD=θ（0<θ<π），相关量就容易表达了. 如图6所示，以O为原点，以OB、OP所在直线为y轴、z轴，建立空间直角坐标系，设AB=2，则P（0，0，3），D（2sinθ，-1+2cosθ，0），所以由OQ∶QD=AO∶DC=1∶2，知OQ=13OD，求得Q（23sinθ，

23cosθ-13，0），QP=（-23sinθ，13-23cosθ，3）， 因为lα，且l⊥AB，所以取l的方向向量为n=（1，0，0），记PQ与l所成角为φ，则cosφ=|cos|=sinθ8-cosθ，令8-cosθ=t，t∈（7，9），则cosθ=8-t，所以cos2φ=-t2+16t-63t=16-（t+63t）≤16-67，当且仅当t=37时等号成立，即（cos2φ）max=16-67，从而（tanφ）min=3+372，故选B.

例4 如图7所示，在矩形ABCD中，AB=2，AD=1，M为AB的中点，将△ADM沿DM翻折，在翻折过程中，当二面角A-BC-D的平面角最大时，其正切值為（  ）.

A.33  B.12  C.23  D.14

解析 在图7中，过A做DM的垂线，垂足为E，交CD于F，交BC的延长线于G，在图8中，设A在平面BCD内的射影为O，则随着翻折，点O在直线EG上运动，过O做BC的垂线，垂足为H，连接AH，则∠AHO为二面角A-BC-D的平面角，设∠AEO=θ（0<θ<π），由AE=

22，得AO=AEsin θ=22sin θ，在图7中，由∠GAB=45°，可得AG=22，则OG=22-22-22cos θ=22-22（1+cos θ），OH=22OG=2-12（1+cos θ），即有tan∠AHO=AOOH=

22sinθ2-12（1+cosθ）=2·sinθ3-cosθ（0<θ<π），令t=sinθ3-cosθ，0<θ<π，可得sin θ+tcos θ=3t≤

t2+1，解得t≤

24，则tan∠AHO≤12.所以当二面角A-BC-D的平面角最大时，其正切值为12，故选B.

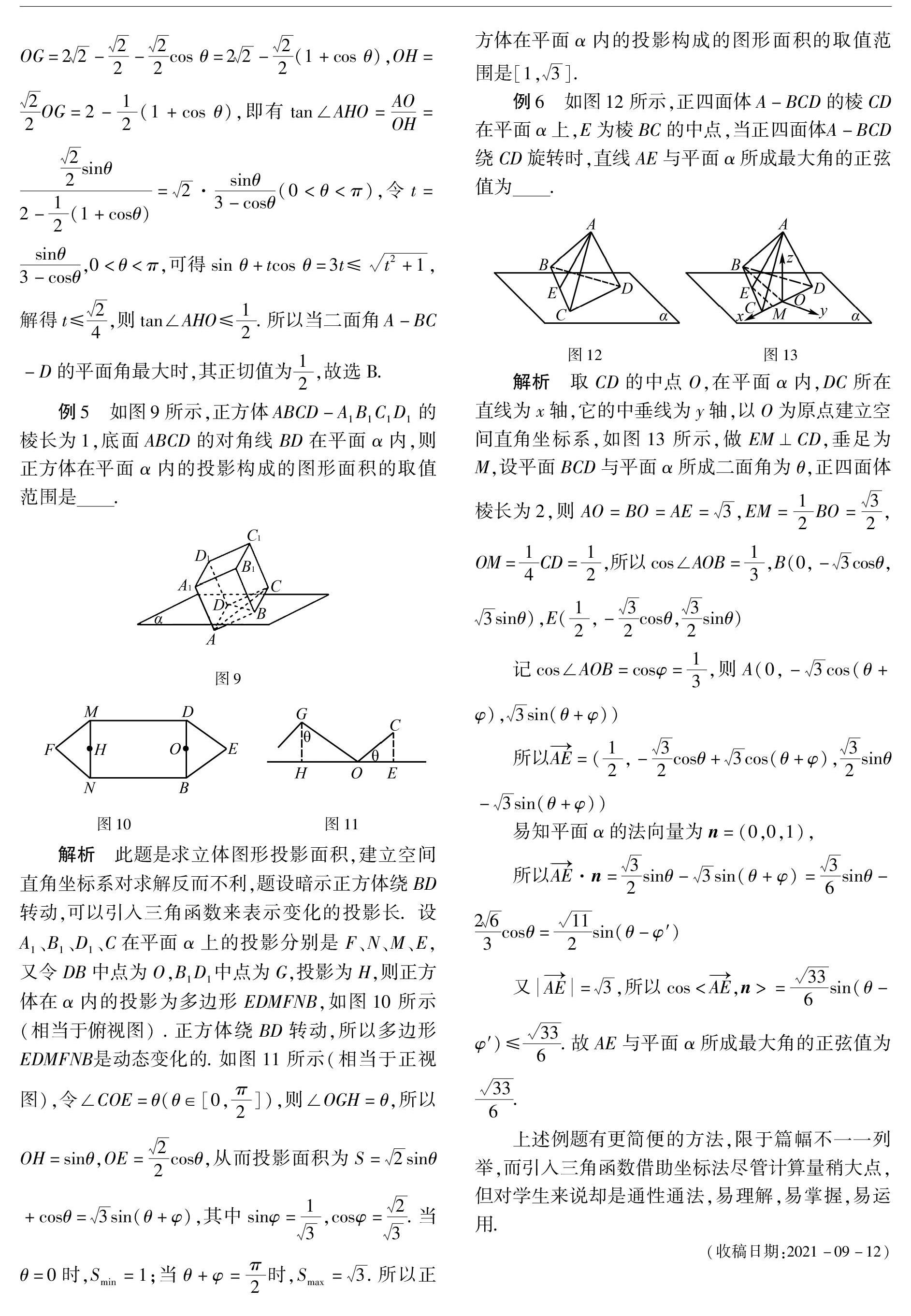
例5 如图9所示，正方体ABCD-A1B1C1D1的棱长为1，底面ABCD的对角线BD在平面α内，则正方体在平面α内的投影构成的图形面积的取值范围是.图9

解析 此题是求立体图形投影面积，建立空间直角坐标系对求解反而不利，题设暗示正方体绕BD转动，可以引入三角函数来表示变化的投影长. 设A1、B1、D1、C在平面α上的投影分别是F、N、M、E，又令DB中点为O，B1D1中点为G，投影为H，则正方体在α内的投影为多边形EDMFNB，如图10所示（相当于俯视图） .正方体绕BD转动，所以多边形EDMFNB是动态变化的.如图11所示（相当于正视图），令∠COE=θ（θ∈[0，π2]），则∠OGH=θ，所以OH=sinθ，OE=22cosθ，从而投影面积为S=2sinθ+cosθ=3sin（θ+φ），其中sinφ=13，cosφ=23.当θ=0时，Smin=1;当θ+φ=π2时，Smax=3.所以正方体在平面α内的投影构成的图形面积的取值范围是[1，3].

例6 如图12所示，正四面体A-BCD的棱CD在平面α上，E为棱BC的中点，当正四面体A-BCD绕CD旋转时，直线AE与平面α所成最大角的正弦值为.

解析 取CD的中点O，在平面α内，DC所在直线为x轴，它的中垂线为y轴，以O为原点建立空间直角坐标系，如图13所示，做EM⊥CD，垂足为M，设平面BCD与平面α所成二面角为θ，正四面体棱长为2，则AO=BO=AE=3，EM=12BO=32，OM=14CD=12，所以cos∠AOB=13，B（0，-3cosθ，3sinθ），E（12，-32cosθ，32sinθ）

记cos∠AOB=cosφ=13，则A（0，-3cos（θ+φ），3sin（θ+φ））

所以AE=（12，-32cosθ+3cos（θ+φ），32sinθ-3sin（θ+φ））

易知平面α的法向量为n=（0，0，1），

所以AE·n=32sinθ-3sin（θ+φ）=36sinθ-263cosθ=112sin（θ-φ′）

又AE=3，所以cos=336sin（θ-φ′）≤336.故AE与平面α所成最大角的正弦值为336.

上述例题有更简便的方法，限于篇幅不一一列举，而引入三角函数借助坐标法尽管计算量稍大点，但对学生来说却是通性通法，易理解，易掌握，易运用.

（收稿日期：2021-09-12）