研究极值点偏移问题的新方法

关于极值点偏移问题，已有很多相应的高考题及相应的文献给予了深入研究，本文将从“增长速度的快慢即导数的大小”方面研究该问题.

题1 求证：（1）若0≤x≤e，则（e-x）e+x≤（e+x）e-x（当且仅当x=0时取等号）;

（2）若0≤x2≤x1≤e，则（e-x1）e+x2≤（e+x2）e-x1（当且仅当x1=x2=0时取等号）;

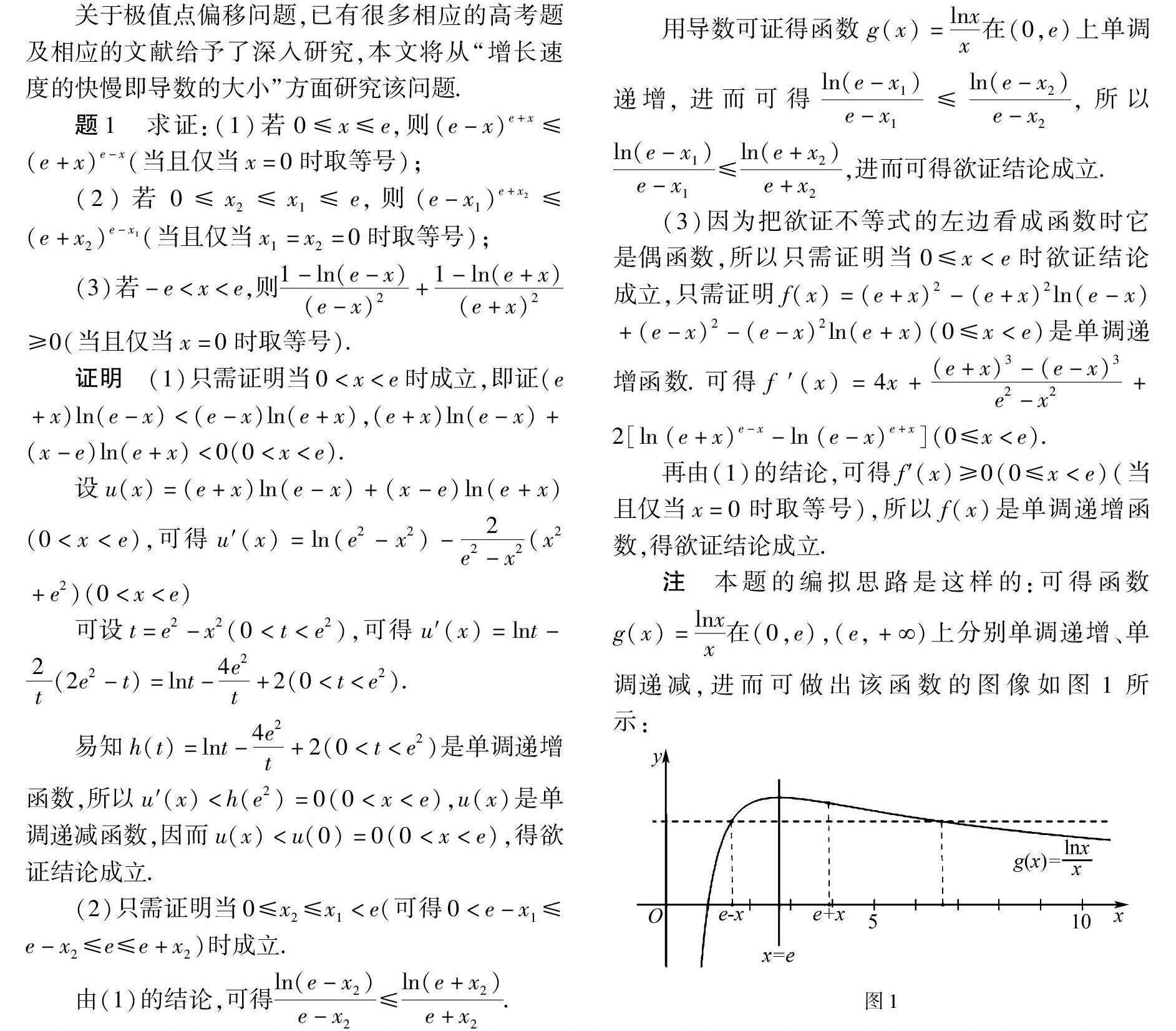
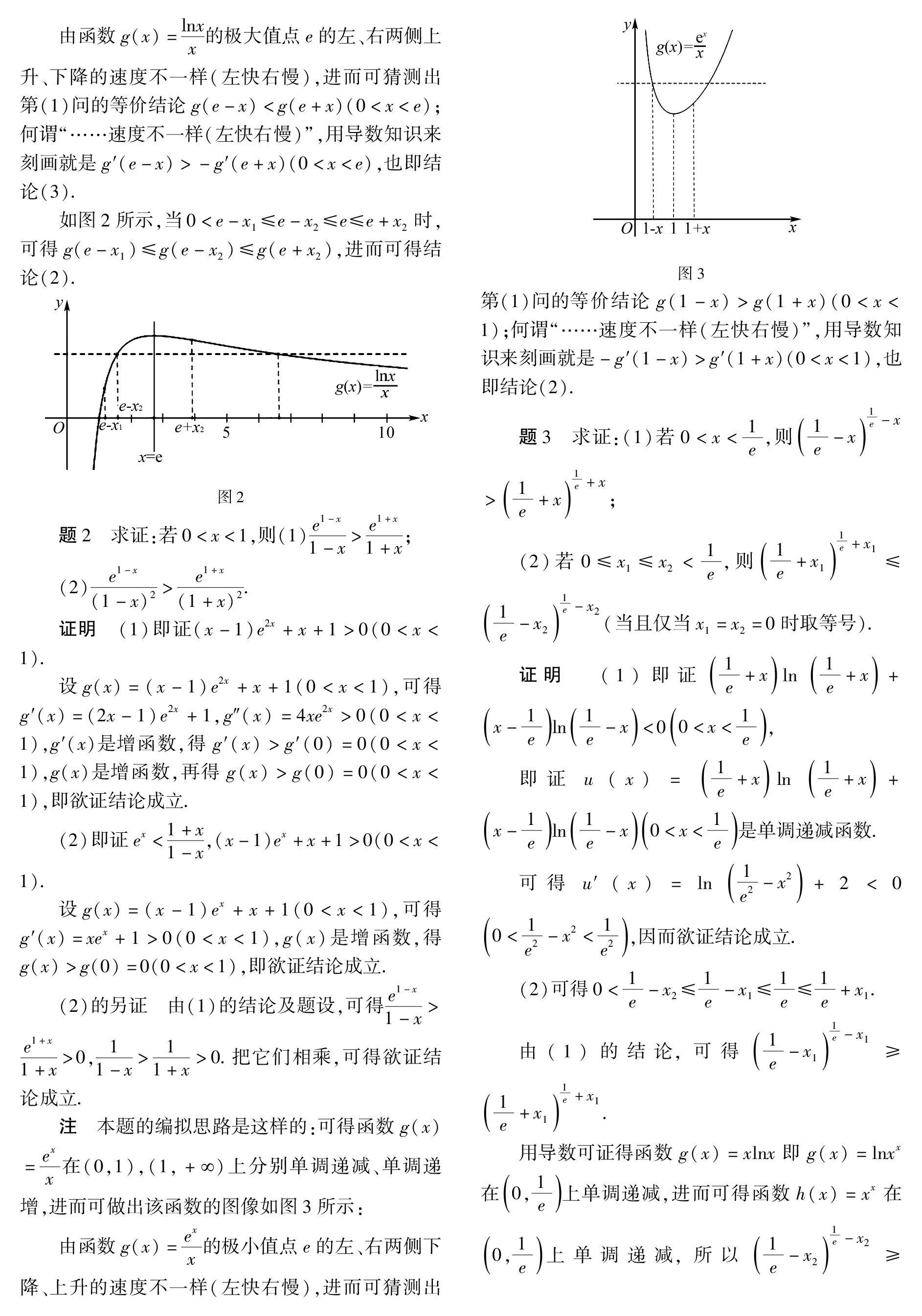
（3）若-e

证明 （1）只需证明当0

设u（x）=（e+x）ln（e-x）+（x-e）ln（e+x）（0

u′（x）=ln（e2-x2）-2e2-x2（x2+e2）（0

可设t=e2-x2（0

易知h（t）=lnt-4e2t+2（0

（2）只需证明当0≤x2≤x1

由（1）的结论，可得ln（e-x2）e-x2≤ln（e+x2）e+x2.

用导数可证得函数g（x）=lnxx在（0，e）上单调递增，进而可得ln（e-x1）e-x1≤ln（e-x2）e-x2，所以ln（e-x1）e-x1≤ln（e+x2）e+x2，进而可得欲证结论成立.

（3）因为把欲证不等式的左边看成函数时它是偶函数，所以只需证明当0≤x

再由（1）的结论，可得f′（x）≥0（0≤x

注 本题的编拟思路是这样的：可得函数g（x）=lnxx在（0，e），（e，+SymboleB@）上分别单调递增、单调递减，进而可做出该函数的图像如图1所示：

由函数g（x）=lnxx的极大值点e的左、右两侧上升、下降的速度不一样（左快右慢），进而可猜测出第（1）问的等价结论g（e-x）-g′（e+x）（0

如图2所示，当0

题2 求证：若0e1+x1+x;

（2）e1-x（1-x）2>e1+x（1+x）2.

证明 （1）即证（x-1）e2x+x+1>0（0

设g（x）=（x-1）e2x+x+1（0

g′（x）=（2x-1）e2x+1，g″（x）=4xe2x>0（0

g′（x）是增函数，得g′（x）>g′（0）=0（0

g（x）是增函数，再得g（x）>g（0）=0（0

（2）即证ex<1+x1-x，（x-1）ex+x+1>0（0

设g（x）=（x-1）ex+x+1（0

g′（x）=xex+1>0（0g（0）=0（0

（2）的另证 由（1）的结论及题设，可得e1-x1-x>e1+x1+x>0，11-x>11+x>0.把它们相乘，可得欲证结论成立.

注 本题的编拟思路是这样的：可得函数g（x）=exx在（0，1），（1，+SymboleB@）上分别单调递减、单调递增，进而可做出该函数的图像如图3所示：

图3

由函数g（x）=exx的极小值点e的左、右两侧下降、上升的速度不一样（左快右慢），进而可猜测出第（1）问的等价结论g（1-x）>g（1+x）（0g′（1+x）（0

题3 求证：（1）若01e+x1e+x;

（2）若0≤x1≤x2<1e，则1e+x11e+x1≤1e-x21e-x2（当且仅当x1=x2=0时取等号）.

证明 （1）即证1e+xln1e+x+x-1eln1e-x<00

即证u（x）=1e+xln1e+x+x-1e

ln1e-x0

可得u′（x）=ln1e2-x2+2<00<1e2-x2<1e2，因而欲证结论成立.

（2）可得0<1e-x2≤1e-x1≤1e≤1e+x1.

由（1）的结论，可得1e-x11e-x1≥1e+x11e+x1.

用导数可证得函数g（x）=xlnx即g（x）=lnxx在0，1e上单调递减，进而可得函数h（x）=xx在0，1e上单调递减，所以1e-x21e-x2≥1e-x11e-x1，进而可得欲证结论成立.

由以上思路，笔者还得到了下面的四个结论：

定理1 若f（x）在（a，x0]，[x0，b）上分别是增函数、减函数，f（x1）=f（x2）（a

g（u）在（a，x0]上是增函数f（x1）2x0f（x2）>f（2x0-x2）g（u）在[x0，b）上是增函数

证明 由题设，可得g（u）在（a，x0]上是增函数g（x1）

f（2x0-x1）x02x0-x1>ax1+x2>2x0>ax1>2x0-x2>aa

f（x1）>f（2x0-x2）f（x1）=f（x2）f（x2）>f（2x0-x2）g（x2）>g（x0）g（u）在[x0，b）上是增函数，

所以欲证结论成立.

定理2 若f（x）在（a，x0]，[x0，b）上分别是增函数、减函数，f（x1）=f（x2）（a

f（2x0-x1）x1+x2<2x0f（x2）

证明 同定理1可证.

定理3 若f（x）在（a，x0]，[x0，b）上分别是减函数、增函数，f（x1）=f（x2）（a

f（2x0-x1）x1+x2>2x0f（x2）

证明 在定理1中设h（x）=-f（x），可得欲证结论成立.

定理4 若f（x）在（a，x0]，[x0，b）上分别是减函数、增函数，f（x1）=f（x2）（a

f（2x0-x1）x1+x2<2x0f（x2）>f（2x0-x2）g（u）在[x0，b）上是增函数.

证明 在定理2中设h（x）=-f（x），可得欲证结论成立.

注 把定理1～4中的“a”换为“-SymboleB@”或“b”换为“+SymboleB@”后，所得结论也成立.由定理1～4还可编拟出很多题目.

题4 已知函数f（x）=xe-x（x∈R）.

（1）（2010年高考天津卷理科第21（3）题）若x1≠x2，f（x1）=f（x2），求证：x1+x2>2;

（2）求证：g（u）=f（u）-f（2-u）（u>1）是增函数.

注 由本题（2）结论及定理1可得本题（1）结论.

题5 已知函数f（x）=1-x1+x2ex.

（1）（2013年高考湖南卷文科第21（2）题）证明：当

f（x1）=f（x2）（x1≠x2）时，求证：x1+x2<0;

（2）求证：g（u）=f（u）-f（-u）（u>0）是减函数.

注

由本题（2）结论及定理2可得本题（1）结论.

题6 已知函数f（x）=（x-2）ex+a（x-1）2（a>0）有两个零点.

（1）（2016年高考全国卷Ⅰ理科第21（2）题）设x1，x2是f（x）的两个零点，证明：x1+x2<2;

（2）求证：g（u）=f（u）-f（2-u）（u>1）是增函数.

注

由本题（2）结论及定理4可得本题（1）结论.

题7 已知函数f（x）=x（1-lnx）.

（1）（2021年新高考全国卷I第22（2）题部分结论的等价问题）若f（x1）=f（x2）（02;（2）求证：g（u）=f（u）-f（2-u）（0

注

由本题（2）结论及定理1可得本题（1）结论.

题8 已知函数f（x）=xlnx.

（1）若f（x1）=f（x2）02e;

（2）求证：g（u）=f（u）-f2e-u0

注

由本题（2）结论及定理3可得本题（1）结论.

题9 已知函数f（x）=lnx+1x.

（1）若f（x1）=f（x2）1e2;

（2）求证：g（u）=f（u）-f（2-u）1e

注

由本题（2）结论及定理3可得本题（1）结论.

基金项目：本文系北京市教育学会“十三五”教育科研滚动立项课题“数学文化与高考研究”（课题编号FT2017GD003，课题负责人：甘志国）阶段性研究成果之一.

（收稿日期：2021-09-10）