活用长方体模型巧解立体几何问题

潘敬贞 蔡海涛

(1.广东省佛山市顺德区容山中学 528303；2.福建省莆田市莆田第二中学 351131)

《高中数学课程标准(2017版)》强调在立体几何教学中，要充分借助长方体的模型功能，通过直观感知，认识和理解空间点、直线、平面的位置关系，并抽象出空间点、直线、平面的位置关系的定义，进而解决有关问题，这是立体几何解题中常用的“模型化思想”，其关键是通过模型识别或模型构建，将问题化归转化，使问题轻松获解，而识别或构建长方体模型，常用“割补法”.本文例谈借助长方体模型解决立体几何中点线面位置关系的定性及定量问题，期与同行交流.

一、活用长方体模型解决定性问题

1.平行问题

例1(2019全国Ⅱ文7)设α，β为两个平面，则α∥β的充要条件是( ).

A.α内有无数条直线与β平行

B.α内有两条相交直线与β平行

C.α，β平行于同一条直线

D.α，β垂直于同一平面

解析构造长方体如图1，对于A选项，设平面A1ADD1为α，设平面ABCD为β，在平面α内与直线AD平行的直线都与平面β平行，而在平面α内有无数条直线与直线AD平行，即平面α内有无数条直线与平面β平行，但平面α与平面β相交，故A选项错误；根据面面平行的判定定理可知B选项正确；对于C选项，设平面ABCD为α，设平面C1CDD1为β，由图1可知A1B1∥α，A1B1∥β，但平面α与平面β相交，故C选项错误；对于D选项，设平面A1ADD1为α，设平面C1CDD1为β，由图1可知α⊥平面ABCD，β⊥平面ABCD，但平面α与平面β相交，故D选项错误.

2.垂直问题

例2(2019北京卷文13理12)已知l，m是平面α外的两条不同直线．给出下列三个论断：①l⊥m；②m∥α；③l⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题____.

解析构造长方体如图1，设平面ABCD为α，A1A1=l，A1B1=m，再由线面平行的判定定理可得：若l⊥α，l⊥m，则m∥α，故答案为：若l⊥α，l⊥m，则m∥α.

评注要正确判断点、线、面的位置关系，不仅需要对立体几何必备知识的熟练掌握，而且还需要具有较高的数学素养水平，尤其是直观想象素养.当碰到元素比较多时，想根据题意作相应的直观图就显得比较困难，因此在考场上欲全凭想象能力解决此类问题难度就比较，但如果能够借助长方体模型，此问题的解答就容易很多，通过构建长方体就可以逐个验证选项正确与否，解题效率也就大大提高.

二、活用长方体模型解决定量问题

1.求表面积

例3 (2015安徽卷)一个四面体的三视图如图所示，则该四面体的表面积是( ).

图2

评注已知某几何体的三视图，求几何体的有关问题，解答此类问题一般需要经过还原几何体再进行求解，如果几何体是简单的多面体(非旋转体)都建议构造长方体或正方体模型辅助求解，活用长方体或正方体模型辅助求解此类问题可以大大的降低试题解答难度，提高解题效率.

2.求角

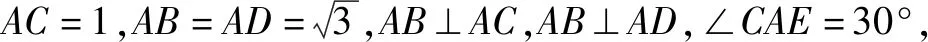
3.求距离

评注求空间角问题、距离问题等定量问题对学生的空间想象能力、逻辑推理能力、运算求解能力等能力要求比较高，但如果能够借助长方体模型，根据题意构造合适的长方体对解决定量问题有很大的帮助，可以有效降低思维难度，提高解题效率.

在解题过程中要善于挖掘题目条件，联系长方体正方体的性质以及长方体正方体中特殊的位置关系与数量关系，只有这样方可提高解题能力，提高解题效率.

合理构建模型有助于学生能在不同的问题情境中发掘出数学内容的共性，笔者认为这就是问题的“数学本质”，有别于其它数学问题的基本特质，从而便能揭示其问题的内涵.因此，长方体模型成为学生认识空间几何体的“源”，是处理立体几何问题的根基.在解有关立体几何问题时，要结合“割补”这一重要的数学方法，充分利用长方体模型进行解题，可降低试题解答难度，快速有效地解决问题，提高解题效率，有利于激发学生的学习兴趣，发展学生直观想象、抽象概括、数学运算等核心素养等.