如何利用法向量确定二面角是锐角还是钝角
——从一道题目谈起
2021-10-20 09:21徐加华李霞和法文
数理化解题研究 2021年28期
徐加华 李霞 和法文
(山东省新泰市第一中学 271200)
一、前言
我们知道,二面角的平面角与两个平面的法向量的夹角相等或互补.那么到底什么情况下相等,什么情况下互补呢?2020年5月投入使用的普通高中教科书数学选择性必修第一册也没有给出相应的判断方法,而是采用将问题改成求平面的夹角来回避这个问题.
二、引例解析
我们先看摘自薛金星老师主编的《解透教材·高中数学选择性必修第一册(RJ·A)》第85页上的一道题目:如图1在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点.∠DAB=90°,AB∥CD,AD=CD=2AB=2.
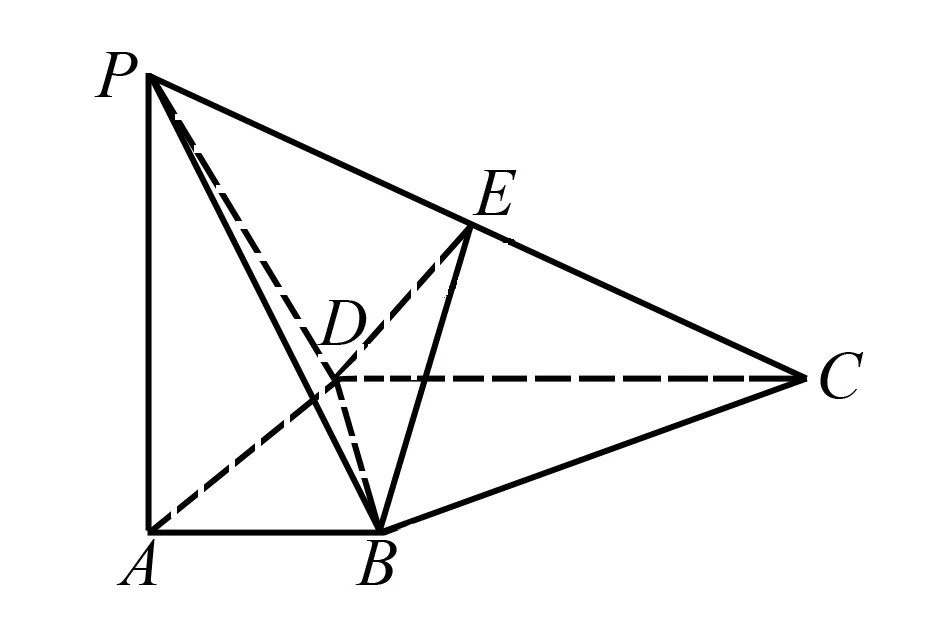
图1
(1)求证:平面PA⊥平面ABCD.
(2)若二面角E-BD-P大于60°,求四棱锥P-ABCD体积的取值范围.
我们先看资料给出的答案:
(1)证明 ∵∠DAB=90°,∴AB⊥AD.∵平面PAD⊥平面ABCD,∴AB⊥平面PAD,∴AB⊥PA.∵PA⊥BC,AB∩BC=B,∴PA⊥平面ABCD.
(2)解如图2,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴,建立空间直角坐标系.

图2
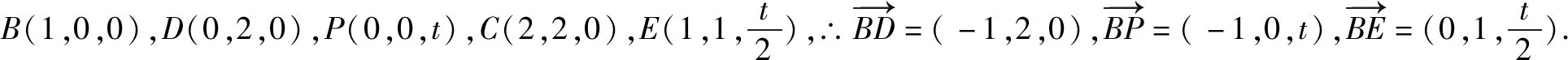


1.基本常识


图3
2.基本结论

3.结论证明
已知m,n分别是平面α,β的法向量,设M,N分别是平面α,β内的点,且两点都不在平面α与β的交线l上,二面角α-l-β的大小为θ,


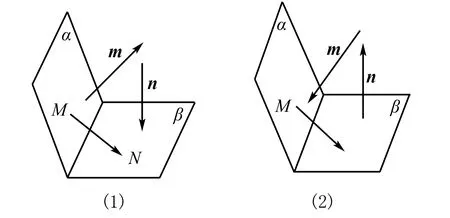
图4



图5

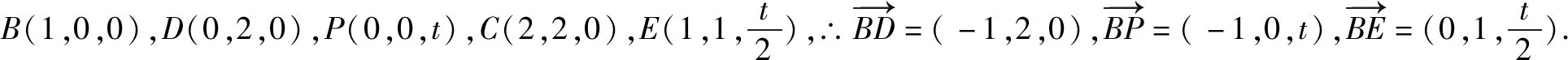
猜你喜欢
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26
新世纪智能(数学备考)(2021年4期)2021-08-06
中学生数理化·高一版(2021年1期)2021-03-19
中学生数理化(高中版.高考数学)(2020年3期)2020-05-25
中学生理科应试(2019年3期)2019-07-08
高中生·天天向上(2018年1期)2018-04-14
中学数学研究(广东)(2018年23期)2018-03-05
求知导刊(2017年30期)2018-01-17
广东教育·高中(2017年7期)2017-09-01
福建中学数学(2016年2期)2016-10-19

